- Учителю
- Урок информатики в 9 классе по теме 'Заполнение одномерного массива последовательностью чисел Фибоначчи'
Урок информатики в 9 классе по теме 'Заполнение одномерного массива последовательностью чисел Фибоначчи'
Открытый интегрированный урок в 9 «А» классе
Дата: 29.10.10
Тема: Заполнение одномерного массива последовательностью чисел Фибоначчи
Цели:
Образовательные:
-
Дать понятие термина «Последовательность чисел Фибоначчи»;
-
Учить применять последовательности этих чисел при решении задач на заполнение и обработку одномерных массивов;
-
Способствовать осуществлению межпредметных связей на уроке информатики.
Развивающие:
-
Развивать навыки заполнения массива при помощи формул;
-
Способствовать развитию логического и алгоритмического мышления путем выполнения практической работы;
-
Развивать познавательный интерес и творческую активность.
Воспитательные:
-
Воспитывать культуру общения в группах;
-
Повышать интерес к историческим событиям, связанным с числами последовательности Фибоначчи.
Тип урока: изучение нового материала и закрепление ранее изученного.
Вид урока: комбинированный.
Основные методы, технологии: элементы объяснительно-иллюстративного метода; частично-поискового; наглядный (демонстрация компьютерной презентации); практического; элементы групповой технологии, информационная технология.
Ход урока
-
Организационный момент
Приветствие. Определение отсутствующих. Проверка готовности учащихся к уроку.
Объявление цели урока обучающимся: научиться заполнять одномерные массивы последовательностью чисел Фибоначчи.
-
Актуализация опорных знаний
На сегодняшнем уроке, ребята, нам с вами понадобится вспомнить ранее изученные понятия. Для этого давайте проведем операторный диктант по вариантам. Возьмите оценочные листы, которые лежат у вас на столах. Подпишите свою фамилию и имя. Проставьте ответы на вопросы в соответствующие ячейки таблицы.
1 вариант
2 вариант
1. Что такое массив?
1. Что называется индексом массива?
2. Форма описания одномерного массива
2. Алгоритм вывода одномерного массива
3. Оператор цикла с параметром
3. Оператор присвоения
4. Дайте определение одномерного массива
4. Дайте определение двумерного массива
5. Оператор вывода данных
5. Оператор ввода данных
А теперь, внимание, правильные ответы:
1 вариант
2 вариант
1. Массив - это совокупность конечного числа элементов одного и тог же типа
1. Номер элемента массива называется его индексом.
2. Var имя_массива: array [n1..n2] of тип элементов
2. For I:= 1 to n do
Write (a[i]: 5);
3. For i:= n1 to/downto n2 do оператор
3. Переменная := выражение
4. Массив с одним индексом называется одномерным
4. Массив с двумя индексами называется двумерным
5. Write (a1, a2, …, an)
WriteLn (a1, a2, …, an)
-
Read (a1, a2, …, an)
ReadLn (a1, a2, …, an)
В оценочный лист поставьте себе:
5 баллов - верно ответили на 5 вопросов;
4 балла - верно ответили на 4 вопроса;
3 балла - верно ответили на 3 вопроса;
2 балла - верно ответили на 2 вопроса.
3. Объяснение нового материала
Запишите в рабочую тетрадь сегодняшнее число, тему урока. Давайте вспомним, какие способы заполнения одномерного массива вы знаете?
Способ заполнения массива с клавиатуры, при помощи датчика случайных чисел. На уроках мы с вами использовали только первых два способа. Сегодня мы с вами будем заполнять массив по формуле. Мы будем заполнять массив числами Фибоначчи. Но сначала разберемся что это за интересные числа.
Ребята, а вы когда-нибудь слышали о Леонардо Фибоначчи?
Тогда прослушайте небольшую историческую справку.
Леонардо из Пизы, известный как Фибоначчи, был первым из великих математиков Европы позднего Средневековья. Будучи рожденным в Пизе в богатой купеческой семье, он пришел в математику благодаря сугубо практической потребности установить деловые контакты. В молодости Леонардо много путешествовал, сопровождая отца в деловых поездках. Например, мы знаем о его длительном пребывании в Византии и на Сицилии. Во время таких поездок он много общался с местными учеными.
Числовой ряд, носящий сегодня его имя, вырос из проблемы с кроликами, которую Фибоначчи изложил в своей книге «Liber abacci», написанной в 1202 году:
Человек посадил пару кроликов в загон, окруженный со всех сторон стеной. Сколько пар кроликов за год может произвести на свет эта пара, если известно, что каждый месяц, начиная со второго, каждая пара кроликов производит на свет одну пару?
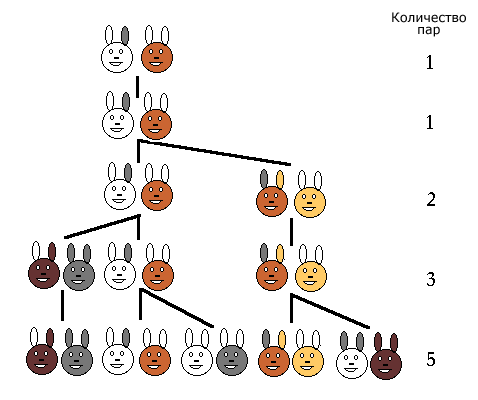
![]()
В средневековой загадке с кроликами, которую загадал Фибоначчи, кроется мистическая последовательность чисел.
Прослушать слайд с комментариями.
Таким образом, Решение этой задачи сводится к бесконечной последовательности чисел.
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 …
В тетрадях: Последовательность чисел, первые два числа которой равны 1, а каждый последующий член (начиная с третьего) равен сумме двух предыдущих, называют последовательностью Фибоначчи, а сами числа числами Фибоначчи.
Последовательность Фибоначчи - это не просто игра с числами, а самое важное математическое выражение природных явлений из всех когда-либо открытых.
Эти числа возникают в самых разных математических ситуациях - комбинаторных, числовых, геометрических. Если вы любите отыскивать числовые закономерности в живой природе, то заметите, что числа Фибоначчи встречаются и там. Чешуйки на еловой шишке, ячейки на ананас и семена подсолнечника расположены спиралями, причем количество спиралей каждого направления так же, как правило, числа Фибоначчи.
Давайте вернемся к нашей задаче. Кто сможет ответить на вопрос задачи: Сколько пар кроликов родится за один год.
Еще числа Фибоначчи обладают следующими свойствами:
-
каждое третье число Фибоначчи четное,
-
каждое пятнадцатое оканчивается нулем,
-
для каждого p числа Фибоначчи, делящиеся на p, встречаются периодически,
-
два соседних числа Фибоначчи взаимно просты и др.
А теперь, давайте научимся использовать эту последовательность при решении задач на заполнение и обработку одномерных массивов.
4. Решение задач.
Сначала напишем решение этой задачи. Рассмотрим блок-схему решения алгоритма решения этой задачи:
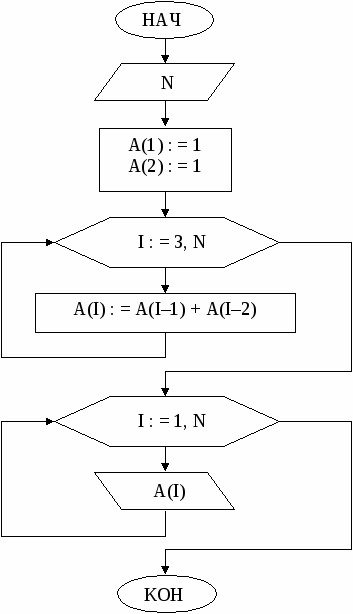
Программа:
Program Fib;
Uses crt;
const n=12;
var А: array [1..n] of integer;
i: integer;
begin
clrscr;
А[1]:=1; А[2]:= 1;
for i:= 3 to n do
А[i]:= А[i-1] + А[i-2];
For i:= 1 to n do
write (A[i]:5);
readln;
end.
1
1
2
3
5
8
13
21
34
55
89
144
янв
фев
март
апр
май
июнь
июль
авг
сен
окт
нояб
дек
Ответ: 144 кролика. Видите какой доход можно получить, выращивая кроликов.
-
Минутка отдыха
А сейчас, ребята, давайте немного отдохнем. Возьмите листочки и запишите любых два числа в столбик. Затем дополните эти числа по принципу чисел Фибоначчи. То есть, каждое последующее число получается сложением предыдущих двух чисел. Заполните столбик до тех пор, пока не будет 10 чисел. А сейчас дайте мне листочек, я быстро в уме сосчитаю, сколько получится.
-
Работа в группах на компьютерах
Итак, отдохнули, сейчас разбиваемся на группы по шесть человек.
За каждым компьютером находится задача, которую вы должны решить на компьютере.
1 группа: Заполнить одномерный массив A(N) элементами последовательности Фибоначчи. Найти сумму первых K элементов.
2 группа: Дана последовательность Фибоначчи A(N). Что больше: сумма четных или произведение нечетных элементов и насколько.
3 группа: Напечатать те элементы массива A(N), индексы которых являются четными числами последовательности Фибоначчи.
4 группа: Заполнить массив A(N) так: первые K элементов заполнить элементами последовательности Фибоначчи, остальным - присвоить число m.
Решение:
1 группа:
Program Fib;
Uses crt;
var a: array [1..100] of integer;
i,k,s: integer;
begin
clrscr;
Writeln ('Введите размерность массива ');
Read (n);
WriteLn ('Последовательность чисел Фибоначчи:');
a[1]:=1; a[2]:= 1;
for i:= 3 to n do begin
a[i]:= a[i-1] + a[i-2];
end;
writeLn;
for i:=1 to n do
write (a[i]:5);
WriteLn ('Введите К: ');
readLn (k);
s:= 0;
for i:= 1 to k do
s:= s + a[i];
WriteLn ('Сумма первых ', k, 'элементов = ', s);
readln;
end.
2 группа:
Program Fib;
Uses crt;
var a: array [1..100] of integer;
i, n, p,s: integer;
begin
clrscr;
Writeln ('Введите размерность массива ');
Read (n);
a[1]:=1; a[2]:= 1;
for i:= 3 to n do begin
a[i]:= a[i-1] + a[i-2];
end;
WriteLn ('Последовательность чисел Фибоначчи:');
for i:=1 to n do
write (a[i]:5);
writeln;
s:= 0; p:=1;
for i:= 1 to n do begin
if a[i] mod 2 = 0 then s:= s + a[i]
else p:= p*a[i];
end;
if s>p then WriteLn ('Сумма четных чисел Фибоначчи больше произведения нечетных на ', s-p)
else
WriteLn ('Произведение нечетных чисел Фибоначчи больше суммы четных на ', p-s);
readln;
end.
3 группа:
Program Fib;
Uses crt;
var a: array [1..100] of integer;
I, n, k, s: integer;
begin
clrscr;
Writeln ('Введите размерность массива ');
Read (n);
a[1]:=1; a[2]:= 1;
for i:= 3 to n do begin
a[i]:= a[i-1] + a[i-2];
end;
WriteLn ('Последовательность чисел Фибоначчи:');
for i:=1 to n do
write (a[i]:5);
writeln;
WriteLn ('элементы массива, индексы которых являются четными числами последовательности Фибоначчи: ');
For i:= 1 to n do
if i mod 2 = 0 then
Write (a[i], '-');
Readln;
End.
4 группа:
Program Fib;
Uses crt;
var a: array [1..100] of integer;
I, n, k, m: integer;
begin
clrscr;
Writeln ('Введите размерность массива ');
Read (n);
Writeln ('Введите К ');
Readln (k);
Writeln ('Введите m ');
Readln (m);
a[1]:=1; a[2]:= 1;
for i:= 3 to n do begin
a[i]:= a[i-1] + a[i-2];
end;
WriteLn ('Последовательность чисел Фибоначчи:');
for i:=1 to n do
write (a[i]:5);
writeln;
for i:= k+1 to n do
a[i]:= m;
for i:= 1 to n do
writeLn (a[i], '-');
readLn;
end.
А теперь давайте сверимся с ответами при фиксированных переменных величинах:
1 группа при n = 10, k = 5
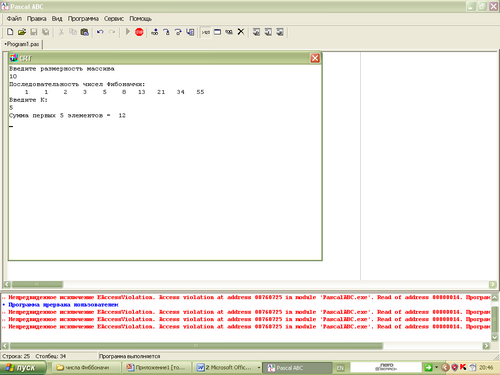
2 группа при n = 10
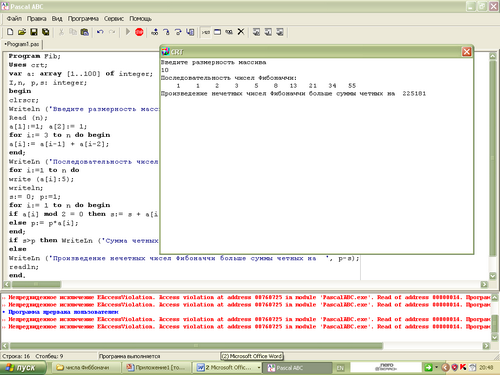
3 группа при n = 10
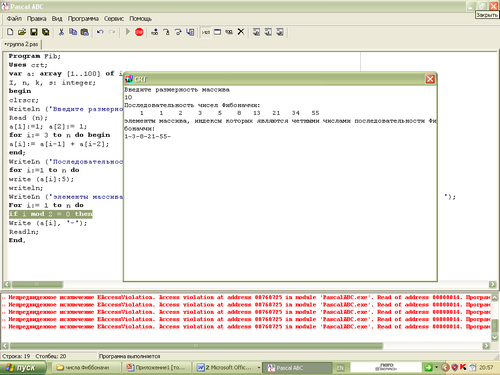
4 группа при n = 10, k = 5, m = 22
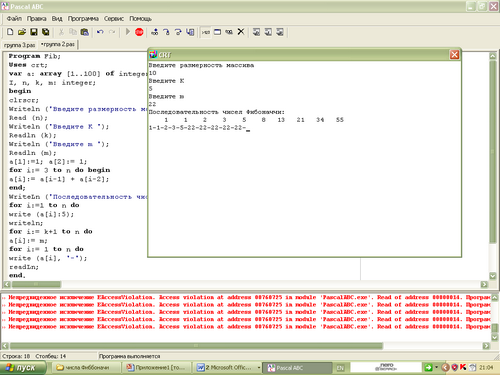
А сейчас, оцените вашу работу на компьютере по шкале:
5 баллов - программа запустилась, работает правильно;
4 балла - программа не запустилась из-за синтаксических ошибок;
3 балла - программа запустилась, но работает неверно;
2 балла - программа не работает.
-
Итог урока.
Выставляйте каждый себе оценку
9-10 и более баллов - оценка «5»
7-8 баллов - оценка «4»;
5-6 баллов - оценка «3».
Ниже тройки на сегодняшнем уроке оценка не выставляется. Будем работать с вами дополнительно.
Домашнее задание: решить задачу: Заполнить массив A элементами последовательности Фибоначчи до тех пор, пока элемент массива A не станет больше числа M. Вывести получившийся массив.
А теперь давайте подведем итоги сегодняшнего урока.
Посчитаем сколько у нас пятерок, четверок, троек. Значит, цели урока мы достигли.
Что нового вы узнали на уроке?
Рефлексия:
Ребята, мы с вами очень плодотворно поработали! Вы неплохо разобрались в теоретическом материале и почти правильно решили все задачи! Молодцы! Мне очень было приятно работать с вами! А вы не могли бы поделиться своими впечатлениями?
Ответьте, пожалуйста, на вопросы рефлексии
1. Что вы ожидали от работы на данном уроке? Сравните свои предварительные цели и реально достигнутые результаты.
2. Какие чувства и ощущения возникали у вас в ходе работы? Что оказалось для вас самым неожиданным?
3. Что вам более всего удалось, какие моменты были выполнены наиболее успешно?
Листы оценивания сдайте мне и я выставлю оценки за урок.
9