Практическая работа Тема: Математическая модель. Расчет геометрических параметров объекта. Задача о склеивании коробки.

Практическая работа

Тема: Математическая модель. Расчет геометрических параметров объекта.

Задача о склеивании коробки.

1. Постановки задачи.

Имеется квадратный лист картона. Из листа по углам вырезают четыре квадрата и склеивают коробку по сторонам вырезов. Какова должна быть сторона вырезаемого квадрата, чтобы коробка имела наибольшую вместимость? Какого размера надо взять лист, чтобы получить из него коробку с заданным максимальным объемом.

Цель моделирования - определить максимальный объем коробки.

2. Содержательное описание объекта моделирования.

Объект моделирования:

• Картонный лист - квадрат со стороной a.

• Коробка с квадратным основанием с длиной стороны c, площадью дна S и объемом V.

• Квадратный вырез с длиной стороны b.

Процедура определения максимального объема коробки:

Проследить, как изменяется объем коробки при изменении размера выреза, который увеличивается от 0 с заданным шагом  b.

Ограничения: размер дна не может быть отрицательным (С>0).

Р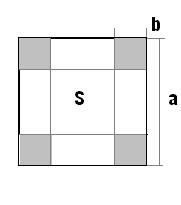азработка модели. Для вывода формул математической модели составим геометрическую модель в виде чертежа с указанием исследуемых характеристик объекта.

Расчетные параметры объекта определяются по формулам:

c=a-2b - длина стороны дна.

S-c² - площадь дна.

V=Sb - объем.

Первоначальный размер выреза b₀=0.

Далее размеры выреза определяются по формуле bi+1=bi+ b.

Компьютерная модель.

Заполняем область исходных данных.

В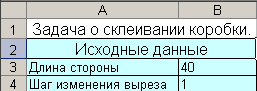

этой области заданы тестовые исходные параметры a=40,  b=1 см, которые используются для расчета «вручную» длины стороны дна, площади дна и объема коробки при нескольких значениях выреза:

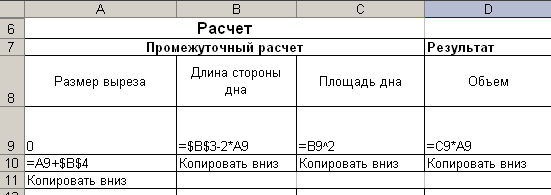
. Составляем таблицу расчета

Здесь ячейка и содержащаяся в ней формула означает:

A9 (0) - начальный размер выреза.

A10 (=A9+$B$4) - следующий размер выреза.

B9 (=$B$3+2*A9) -длина стороны дна.

C9 (=B9*A9) - площадь дна.

D9 (=C9+A9) - объем коробки.

Т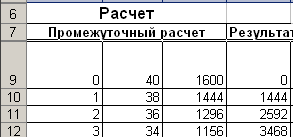естирование. Сравним результаты, полученные после ввода формул, с результатами приведенными в примере расчета:

Совпадение значений с контрольным образцом показывает правильность введения формул.

Проведение исследования.

Исследование параметров модели. (длины стороны дна, площадь дна, объем коробки).

1. Для проведения исследования заполним в компьютерной модели не менее 20 строк.

2. По столбцу В проследим, как изменяется длина стороны дна.. Определим, сколько строк компьютерной модели надо использовать для исследования.

3. Вывод: длина стороны дна уменьшается до нуля, а затем становится отрицательной. Для исследования используем диапазон строк, для которых са/2.

4. В диапазоне строк, подлежащих исследованию, по столбцу С проследим, как изменяется площадь дна.

5. В диапазоне строк, подлежащих исследованию, по столбцу D проследим, как изменяется объем коробки.

6. Вывод: объем коробки сначала увеличивается, достигает некоторого максимального значения, затем уменьшается

Определение наибольшего объема коробки и соответствующего выреза.

В диапазоне строк, подлежащих исследованию, по столбцу D определим наибольший объем коробки. По столбцу А определим размер выреза, соответствующий наибольшему объему.

Зависимость наибольшего объема коробки от размера исходного листа

1. Определим значение наибольшего объема коробки для нескольких значений длины картонного листа. Для этого:

   1. В ячейку В4 введем новое исходное значение.

   2. По столбцу В определим допустимый диапазон строк для исследования. При необходимости заполним дополнительное количество строк.

   3. По столбцу D определим наибольший объем коробки.

   4. По столбцу А определим размер выреза, соответствующий наибольшему объему.

2. Результаты эксперимента разместим в ячейках на свободном пространстве ЭТ по образцу.

   
   
   

   
   
   

   
   
   

   
   
   

   
   
   

   
   
   

   Зависимость наибольшего объема коробки от шага изменения выреза.

   1. Введем в ячейку новое значение шага изменения выреза (например,  b=0,3 см).

   2. Результаты экспериментов разместим в ячейках на свободном пространстве ЭТ по образцу.

   3. сравним значения наибольшего объема и соответствующего выреза, полученные сейчас и в предыдущем эксперименте.

   4. сделайте вывод, позволяет ли уменьшение шага изменения выреза точнее определить наибольший объем и соответствующий вырез.

      Подбор параметров исходного картонного листа

      1. Для подбора размера исходного картонного листа изменяем значение ячейки и определяем наибольший объем коробки, пока не получим заданную величину.

      2. Результаты экспериментов разместим в ячейках на свободном пространстве ЭТ по образцу.

      3. Анализ результатов моделирования. По результатам экспериментов сформулируйте выводы.

      
      
      

      
      
      

      
      
      

      
      
      

      
      
      

      
      
      

      
      
      

      
      
      

      3