Урок информатики в 9 классе «Моделирование геометрических операций и фигур»

Тема урока «Моделирование геометрических операций и фигур»

9 класс

Учитель информатики

ГБОУ лицей №144 Калининского района Санкт-Петербурга

Иванова Ирина Борисовна

Цель: Сформировать знания учащихся о геометрических моделях в жизни человека. Познакомить с алгоритмами построения основных геометрических операций. Сформировать навыки построения геометрических моделей в графическом редакторе Paint.

Задачи:

Образовательные

• формирование навыков работы с программным обеспечением;

• выбор определённого программного средства для реализации, поставленной задачи;

• выработка умений и навыков решения практических задач в соответствующих программах.

Развивающие

• развитие внимания, способности к анализу;

• развитие логического мышления;

• развитие способностей к определённым видам деятельности (дизайн, инженерная графика, программирование и т.д.)

Воспитательные

• формирование самостоятельности мышления, чёткости и организованности в работе, умения контролировать свою деятельность;

• работать эффективно в соответствии с располагаемым временем,

• работать в группе.

Тип урока: комбинированный

Необходимое оборудование: компьютеры, интерактивная доска с программным обеспечением, проектор, рабочий лист группы.

Ход урока:

1. Организационный момент.

Учитель: Тему «Моделирование» мы изучаем уже не первый урок. Мы моделировали различные ситуации, биологические процессы, решали задачи, связанные с математическими расчетами. Модели применяются людьми ещё с глубокой древности, однако лишь в эпоху новых информационных технологий и компьютеризации этот метод исследования приобрел столько разнообразных форм и средств реализации

2. Актуализация знаний.

Учитель: Для работы на уроке нам необходимо вспомнить схему этапов моделирования.

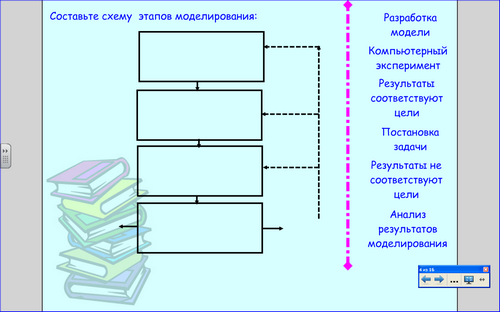
3. Постановка целей и задач урока

Учитель: Я предлагаю послушать несколько выступлений ваших одноклассников, которые поделятся своими наблюдениями

Наблюдение 1. (Бернатович Д)

В информатике много терминов, которые пришли в нее из геометрии. Например, точка (символ, используемый в программах для разделения целой и дробной частей числа), линия (канал связи), цилиндр (совокупность дорожек с одинаковым номером на магнитных дисках), сектор (участок дорожки магнитного диска) и др

Наблюдение 2. Кастрицкая Н.

Задачи на построение возникли в глубокой древности и были связаны с практическими потребностями. Примеры из истории развития геометрии свидетельствуют, что можно добиться точности даже если под рукой нет специальных измерительных инструментов, а есть подсобные предметы: кусок верёвки, ровная палка и т.д. Поэтому необходимо научиться строить модели геометрических фигур с заданными свойствами: равносторонний треугольник, шестиугольник, равнобедренный треугольник и пр. Это можно сделать, используя законы геометрии

Учитель: Спасибо. А теперь объедините все, что увидели и услышали с момента начала урока и попробуйте сформулировать тему нашего урока. (Моделирование геометрических фигур)

Какие цели мы поставим перед собой? (научиться моделировать геометрические фигуры в графическом редакторе)

В каких ситуациях вам может пригодиться такой навык? (для оформления презентаций, вставить в текстовый файл, для подготовки исследовательских работ)

И действительно, в курсе геометрии вы знакомились с темой «Построение геометрических фигур при помощи циркуля и линейки», однако наше время диктует нам использовать все свои знания в цифровом пространстве, поэтому сегодня мы будем создавать модели геометрических фигур в графическом редакторе и строго соблюдать все этапы создания моделей.

Вся история геометрии связана с практикой построения при помощи подручных средств для измерения недоступного. И мы сегодня будем создавать модели в простейшем графическом редакторе, который не требует дополнительной установке, он является стандартным для операционной системы Windows.

4. Объяснение нового материала

• Моделирование объектов с заданными геометрическими свойствами.

• I этап. Постановка задачи.

• Постановка задачи.

Учитель: геометрических фигур существует очень много и построить модели всех на одном уроке невозможно. Посмотрите внимательно на слайд и скажите, как можно назвать такие фигуры? (правильные многоугольники)

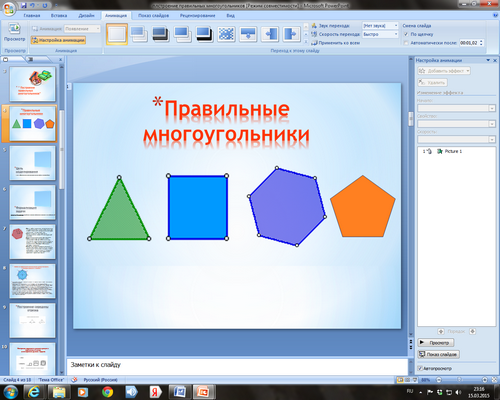
Давайте вспомним особенности правильных многоугольников и подумаем, на каких этапах моделирования они нам могут понадобиться.

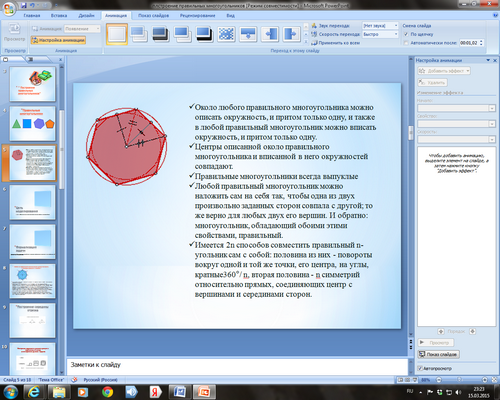
• Цель моделирования

В среде графического редактора научиться моделировать геометрические объекты с заданными свойствами.

• Формализация задачи.

Геометрическая фигура характеризуется длинной сторон и углами, которые необходимо задать в виде отрезков и углов на рабочем поле графического редактора перед началом построения.

• II этап. Разработка алгоритмов для решения задач

Учитель: Перед тем как вы приступите к выполнению построения правильных многоугольников, мы рассмотрим простые построения, которые могут понадобиться вам в процессе работы над заданием.

• МОДЕЛЬ 1. Деление отрезков (моделирование функций линейки) покажет Иванов Дмитрий.

Алгоритм деления отрезка пополам приведён на рисунке 1.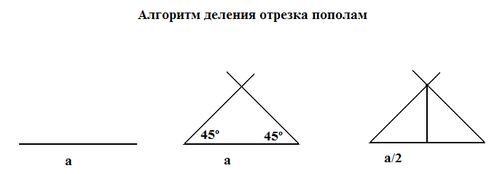

Порядок построения.

1. Копируем данный отрезок.

2. Из концов данного отрезка проводим линии под углом 45 (с помощью клавиши Shift)

3. Из точки их пересечения проводим строго вертикальную линию (с помощью клавиши Shift) до пересечения с данным отрезком.

4. Точка пересечения и есть искомая середина.

Построение основано на том, что высота в равнобедренном треугольнике является одновременно биссектрисой и медианой. Для построения достаточно инструмента Линия и клавиша Shift.

Сохрани построение в Сетевой папке, чтобы им могли пользоваться ребята.

Модель 2. Построение окружности заданного радиуса и определение её центра (моделирование функции циркуля) покажет Веремчук Валентина. Окружность в графическом редакторе вписывается в квадрат со стороной, равной удвоенному радиусу. Алгоритм построение окружности изображен на рисунке

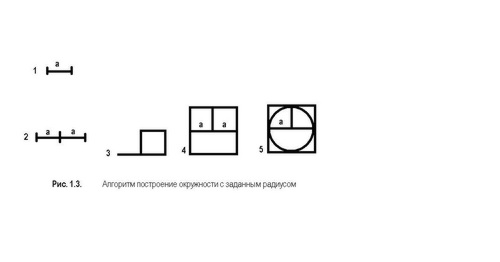
Порядок построения.

1. Копируем данный отрезок а два раза.

2. С помощью стандартной операции (квадрат) строим квадрат со стороной 2а

3. В полученный квадрат, с помощью стандартной операции (окружность) вписываем окружность с радиусом а.

Учитель: Можно убрать дополнительные построения, чтобы такой окружностью можно было бы воспользоваться в процессе работы.

Приступаем к работе в группах. У каждой будет свой модератор. Эти ребята уже предложили свой способ построения и теперь будут координировать ваши действия. На выполнение задания 10 минут.

РОБОТА в ГРУППАХ

Группа 1. Модератор группы Бикчурин Кирилл

1. Разработка моделей

МОДЕЛЬ А. Построение равностороннего треугольника с заданной стороной Данный алгоритм предложил Евклид в IV веке до н.э. Построить треугольник по алгоритму, приведенному на рисунке, и доказать, что полученный треугольник действительно правильный.

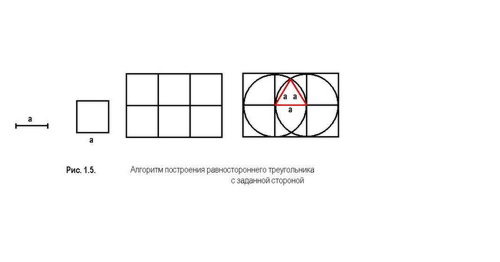
Порядок построения.

1. С помощью стандартной операции (квадрат) строим квадрат со стороной а.

2. Для того чтобы вписать две окружности, проходящие через центр друг друга строи шесть квадратов, вписываем в них две окружности с радиусом а.

3. Точки пересечения окружностей является вершинами треугольника.

Модель В. Построить правильный шестиугольник

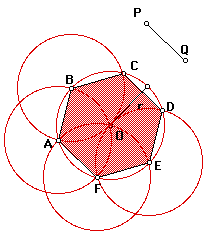
Построение правильного шестиугольника с заданной стороной Используя свойство правильных фигур, вписываются в окружность и то, что сторона равностороннего шестиугольника равна радиусу описанной окружности, выполнить построение по алгоритму на рисунке 1.6. Начать построение окружности с радиусом, равным заданной стороне шестиугольника.

2. Компьютерный эксперимент

Группа 2. Модератор группы Яреха Денис

1. Разработка моделей

МОДЕЛЬ А.

Построение квадрата. Пусть w-данная окружность с центром в точки О и радиусом R. Через точку О проведем диаметр АС и к этому диаметру проведем серединный перпендикуляр, который пересечет окружность w в двух точках В и D.Теперь последовательно соединим точки A,B,C и D. ABCD-искомый квадрат.

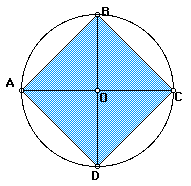
Модель В.

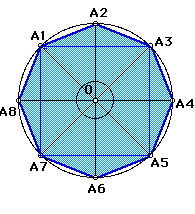
Построение правильного восьмиугольника. Для того, чтобы построить правильный восьмиугольник нужно сначала построить правильный четырехугольник, например, А1А3А5А7-квадрат, потом построить биссектрисы углов А1OА3, А3OА5, А5OА7, А7OА1, которые прересекут окружность в точках А2, А4, А6, А8 соответственно, затем последовательно соединить точки А1,А2,А3,А4,А5,А6,А7,А8. А1А2...А8-искомый восьмиугольник.

2. Компьютерный эксперимент

Группа 3. Модератор группы Бернатович Дарья

Разработка моделей

Построение правильного пятиугольника с заданной стороной

Альбрехт Дюрер (1471-1527гг), ставший олицетворением Возрождения в Германии приводит теоретически точный способ построения правильного пятиугольника, заимствованный из великого сочинения Птолемея "Альмагест". Интерес Дюрера к построению правильных многоугольников отражает использование их в Средние века в арабских и готических орнаментах, а после изобретения огнестрельного оружия - в планировке крепостей

Альбрехт Дюрер не только в рукописях, но также в картинах и книгах оставил многочисленные следы своего математического таланта и увлечение математикой. Об этом свидетельствует знаменитый дюреровский магический квадрат, являющийся одним из самых старых магических квадратов в Европе.

Рассмотрим одно небольшое произведение Дюрера, в котором гениальный художник проводит очень хороший и легкий способ построение правильного пятиугольника с помощью окружности, если известна только длина стороны.

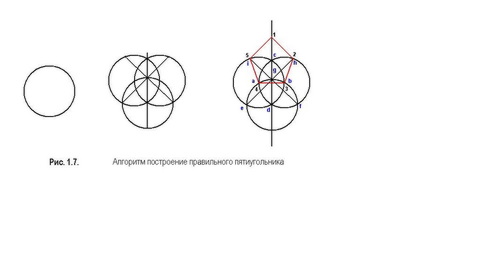
Порядок построения.

Приближенное построение правильного пятиугольника представляет собой интерес. А.Дюрером оно проводится при условии неизменности раствора циркуля, что повышает точность построения. Способ построения описан Дюрером так:"Однако пятиугольник, построенный неизменным раствором циркуля, делай так. Проведи две окружности так, чтобы каждая из них проходила через центр другой. Два центра А и В соедини прямой линией. Это и будет стороной пятиугольника. Точки пересечения окружностей обозначь сверху С, снизу D и проведи прямую линию CD. После этого возьми циркуль с неизменным раствором и, установив одну его ножку в точку D, другой проведи через оба центра А и В дугу до пересечения её с обеими окружностями. Точки пересечения обозначь через E и F, а точку пересечения с прямой CD обозначь буквой G. Теперь проведи прямую линию через Е и G до пересечения с линией окружности. Эту точку обозначь Н. Затем проведи другую линию через F и G до пересечения с линией окружности и поставь здесь J.

Соединив J,A и H,B прямыми, получим три стороны пятиугольника. Дав возможность двум сторонам такой длины достигнуть совпадения в точке K из точек J и H, получим некоторый пятиугольник."

Компьютерный эксперимент

6. Подведение итогов.

Учитель: Молодцы.Все работы групп сохраните в Сетевой папке. Они вам понадобятся для работы.

6. Выставление оценок в журнал.

7. Практическое применения построения правильных многоугольников. Сообщение ученика

6. Постановка домашнего задания. Повторить материал по теме «Моделирование». Найти 3-4 примера правильных многоугольников в природе.

7. Рефлексия. Ответьте в группах на вопросы рефлексии

Все ли получилось? Почему?

___________________________________________

Как менялись чувства и настроение во время урока?

___________________________________________

Лучше всего у нас получилось

___________________________________________

Этого мы достигли благодаря

___________________________________________

Труднее всего было

___________________________________________

Эти трудности мы преодолели так:

___________________________________________

Выполнили поставленные цель и задачи?

___________________________________________

Кто хочет озвучит то, что получилось? (желающие от групп отвечают на вопросы)