Заключительный урок по теме «Основы логики и логические основы устройства компьютера»

Место урока в учебном курсе

В 10 классе провожу следующие уроки по этой теме:

1. Формы мышления. Алгебра высказываний.

2. Логические выражения. Таблицы истинности.

3. Логические функции.

4. Логические законы и правила преобразования логических выражений.

5. Логические основы устройства компьютера.

6. Заключительный урок по теме «Основы логики и логические основы устройства компьютера»

Таким образом, данный урок является заключительно-обобщающим в цикле уроков по теме «Основы логики и логические основы устройства компьютера».

Планируемые образовательные результаты

Предметные: обобщение, систематизация и проверка знаний, усвоенных при изучении темы «Основы логики и логические основы устройства компьютера», интерес к предмету;

Метапредметные: тренировка логического мышления, ИКТ-компетентность;

Личностные: умение работать в группе, навыки самооценивания и взаимного оценивания, ответственность за свою учебную деятельность.

Решаемые учебные задачи:

1. Тестирование учащихся с помощью системы голосования Votum;

2. Работа в группах при решении задач по алгебре логики, систематизированных по уровням сложности и тематике;

3. Самооценивание учащимися знаний по изученному разделу.

Подготовительная работа и необходимое оборудование

• Учащиеся должны быть ранее знакомы с Votum;

• Заполнить таблицу со списком и заданиями (приложение 1);

• Приглашен помощник для подсчёта баллов - учащийся 11 класса;

• Составить таблицу для подсчёта баллов (приложение 2);

• Составить «копилки заданий» (приложение 3);

• Бланки самооценивания (приложение 4);

• ПК учителя, проектор, система Votum.

Ход урока

Этап

урока

На экране

Учитель, пояснения

Ученики, действия

Примерное время работы, мин

Тестирование Votum

Тест в программе Votum (см. приложение 1), по окончанию этапа работы - начинаем заполнять таблицу подсчёта баллов (приложение 2)

Ребята, мы подошли к завершающему уроку по теме «Логика». И сегодня мы должны проверить наши знания по этой теме, оценить их и систематизировать. Первая задача на нашем уроке - «разминка». Каждый ученик одновременно с классом в индивидуальном порядке отвечает на предложенные вопросы с помощью системы голосования. На каждый ответ отведено определённое время. Пожалуйста, посмотрите на экран и приготовьте ваши пульты. Начинаем отвечать при появлении первого вопроса. Время тестирования - 10 минут.

По окончании тестировании мы видим результаты на экране, которые мой помощник перенесёт в таблицу подсчёта баллов.

С помощью системы голосования Votum все учащиеся 10 класса отвечают на предложенные вопросы в порядке индивидуального тестирования.

15

Работа в группах

Заполняется таблица подсчёта баллов (см. приложение 2)

Вторая часть урока - соревнование между группами. В предложенных конвертах - «копилки» заданий. Темы заданий - «Таблицы истинности и логические выражения», «Логические законы и правила преобразования логических выражений», «Логические схемы и логические функции» и «Решение логических задач». Соответственно, одно задание из каждого из этих конвертов может принести команде 1, 2, 3 и 4 балла. За один раз каждый участник из команды может выбрать одно задание, следующее можно взять только если решил предыдущее. Баллы команды складываются из баллов её участников. За 20 минут вы должны набрать возможно большее количество баллов. Команда получает «5» за больше, чем 30 баллов, «4» - если набрано 20-30 баллов, «3» - при количестве 10-19 баллов.

При решении производим с помощником проверку и подсчёт баллов, заполняем таблицу подсчёта.

Учащиеся, разделённые на группы по три-четыре человека, выбирают разделы и уровни заданий, решают задачи из «копилок», набирая общее количество баллов для группы (приложение 3).

25

Самооценивание и подведение итогов урока

Заполняется таблица подсчёта баллов (см. приложение 2)

Мы проверили свои знания, повторили изученную тему. Предлагаю вам с помощью бланков самооценивания самим поставить себе объективную оценку за свои знания и работу на уроке. Эта оценка будет учитываться в общем результате. На эту часть работы - три минуты.

Без комментариев добавляем оценку учащихся к их баллам, вычисляем среднее значение. Делаем вывод о качестве усвоения знаний и работе на уроке, выставляем оценки.

Используя бланки самооценивания (приложение 4), каждый ученик выставляет себе оценку за изучение всего раздела и работу на уроке.

5

Приложения

Приложение 1. Задания для тестирования с помощью Votum

1. Какова формула логического высказывания «Без Вас хочу сказать вам много, При Вас я слушать Вас хочу»?

1. (¬А→В)Ʌ(А→С)

2. (А→В)V(С→D)

3. (А→В)ɅА→С

4. А→ВɅ¬ (C→D)

2. «Наступил сентябрь и начался учебный год» - это суждение:

1. Простое и истинное;

2. Сложное и ложное;

3. Сложное и истинное;

4. Простое и ложное;

5. Суждением не является.

3. Выбрать пример, не являющийся высказыванием:

1. «Гоголь писал «Мёртвые души» в Риме»;

2. «Не можете ли вы передать соль?»;

3. «Рукописи не горят»;

4. «У кошки четыре лапы».

4. Знаком «→» в логике обозначается следующая операция:

1. Конъюнкция;

2. Дизъюнкция;

3. Импликация;

4. Инверсия;

5. Эквиваленция.

5. Покупатель в каждом из магазинов А, В, С. D сделал по одной покупке и приобрёл джойстик, дискеты, бумагу и картридж. Известно, что: джойстик и картридж были куплены не в «А»; в "В " зашел, когда уже купил дискеты и бумагу; в "D" не было ни картриджа, ни бумаги; "С" приехал, уже купив дискеты, а из "D" уходил еще без дискет. ДЖОЙСТИК БЫЛ КУПЛЕН В МАГАЗИНЕ... 1)А 2) В 3) С 4) D

и

и

не

или

не

Функция F в представленной логической схеме принимает значение…

А

F

В

1) 1 2) 0 3)А 4) В

7. Какое из логических выражений, приведённых ниже, имеет значение «0»?

1. (1V1)V(1V0);

2. ((1V0)V1)V1;

3. (0V1)V(1V0);

4. (0&1)&1.

8. Какое тождество записано неверно?

1. X V ¬X=1;

2. X V X V X=1;

3. X&X=X

8. Выражение ¬(АVB)=¬A&¬B…

1) Распределительный закон;

2) Закон де Моргана;

3) Закон идемпотентности;

4) Закон поглощения.

10. Истинность двух высказываний: "неверно, что если магазин А организует распродажу, то и магазин С тоже" и "из двух магазинов В и С организует распродажу только один" означает организацию распродажи в магазинах

1) А,В,С 2) А,В 3) А 4) В,С 5) А,С.

Ответы:

№ вопроса

1

2

3

4

5

6

7

8

9

10

Верный ответ

1

3

2

3

4

2

4

2

2

2

Приложение 2. Таблица для подсчёта баллов

Группа

Ф.И. участника

Разминка, набрано баллов

Работа в группах, набрано баллов

Самооценка в баллах

Итог

I

II

III

Приложение 3. «Копилки заданий»

«Таблицы истинности и логические выражения» (1 балл)

1. Построить таблицу истинности для формулы AV(BV¬B→¬C)

2. Построить таблицу истинности для формулы A&(B&¬B→¬C)

3. Выбрать составное высказывание, имеющее ту же таблицу истинности, что и «не (не А и не (В и С))»:

1. А и В или С и А; 2) (А или В) и (А или С); 3) А и (В или С); 4) А или (не В или не С).

4. Докажите с помощью таблиц истинности равносильность следующих логических выражений: а) (А→В)&(АV¬B); b) (AB)&(A&B)V(¬A&¬B)

5. Какова формула логического высказывания

«Я поеду в Москву и, если встречу там друзей, то мы интересно проведём время»?

1. A /\ (B C)

2. (A /\ B) C \/ D

3. (A /\ B) (C /\ D)

4. A /\ B C

6. Какова формула логического высказывания «Если вы были в Париже, то вы видели Лувр или видели Эйфелеву башню»?

1. A (C /\ D)

2. (A /\ B) C \/ D

3. (A /\ B) (C /\ D)

4. A (C \/ D)

7. Какова формула логического высказывания

«Если вы знаете основы логики, то умеете читать логические схемы и строить таблицы истинности»?

1. (AB) \/ (AC)

2. AB \/ C

3. (AB) /\ AC

4) A(B /\ С)

8. Из приведённых ниже предложений выберите высказывания:

1. Выхожу один я на дорогу.

2. Зачем вы, девушки, красивых любите?

3. Если у вас нет собаки, её не отравит сосед.

4. Давайте восклицать, друг другом восхищаться.

5. Вот кто-то с горочки спустился.

9. Для приведённых ниже высказываний укажите истинные.

1. Число 3 является делителем любого числа, у которого сумма цифр равна 6.

2. Некоторые млекопитающие не живут на суше.

3. Никто не может объять необъятное.

4. Каждый год есть месяц, в котором 13-е число приходится на пятницу.

10. В приведённых ниже высказываниях выделите два простых, обозначьте их буквами и запишите все высказывания с помощью логических операций и этих обозначений.

1. Петя и Коля идут гулять.

2. Петя идёт гулять, а Коля гулять не идёт.

3. Если Коля идёт гулять, то Петя гулять не идёт.

Ответы:

№ вопроса

3

5

6

7

8

9

10

ответ

2

1

4

4

1,3,5

1,2,3,4

АvB

Av¬B

B→¬A

«Логические законы и правила преобразования логических выражений» (2 балла)

1. Упростите следующее выражение и покажите, что оно тождественно-ложное. (A&B&¬B)v(A&¬A)v(B&C&¬C).

2. Упростите следующее выражение и покажите, что оно тождественно-истинное. (A&B&¬С)v(A&B&C)v¬(AvB).

3. Определить значение логического выражения (X>2)→(X>3) дляx=1,2,3,4

4. Определить значение логического выражения ((X<5)→(X<3))&((X<2)→(X<1)) дляx=1,2,3,4

5. Определить значение логического выражения ((X>3)V(X<3))→(X<1) дляx=1,2,3,4

6. При каких значениях Х логическое выражение (X<=2)ИЛИ(X<20)И(X>10) будет истинным?

1. При Х<2;

2. При Х<20;

3. При X>10;

4. При Х=7;

5. При X>2.

6. Каково наибольшее целое положительное число X, при котором истинно высказывание:

(121<Х²)→(Х<Х+5) ?

6. Каково наибольшее положительное целое число Х, при котором ложно высказывание:

(Х(Х+6)+9>0)→(X²>45)?

6. Каково наибольшее целое положительное число X, при котором истинно высказывание:

(Х²-1>100)→(X(Х-1)<100) ?

6. Каково наибольшее положительное целое число Х, при котором ложно высказывание:

(7Х-3<75)→(X(X-1)>65)?

Ответы:

№ вопроса

3

4

5

6

7

8

9

10

ответ

1,1,0,1

0,1,0,0

0,0,1,0

1

11

6

10

8

«Логические схемы и логические функции» (3 балла)

1. Какое количество базовых логических элементов образуют оперативную память компьютера объёмом 64 Мбайта?

2. По заданной логической функции F(A,B)=B&¬Av¬B&A построить логическую схему.

Структурная формула для логической схемы

А

В

С

F

V

&

¬

имеет вид _ _ _ _ _ _ _ _

1) А С В 2) А С В 3) А С В 4) А В С 5) А С В.

4. На входе логической схемы

А

В

С

F

V

&

¬

при F=1 невозможна следующая комбинация сигналов (A, B, C):

1) (0; 0; 1) 2) (0; 1; 0) 3) (0; 1; 1) 4) (1; 0; 0) 5) (0; 0; 0)

5. Дано логическое выражение: не (X1& (X2 V X3) & X4). Нарисовать для него схему и таблицу истинности.

6. Нарисуйте логическую схему для логического выражения X1 & X2 V не X1 & X3

7. Нарисуйте логическую схему для логического выражения X4&(X1&X2 & X3 V не X2&не X3)

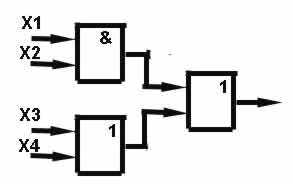
8-9. Задания: для данных логических схем написать логические выражения.

.

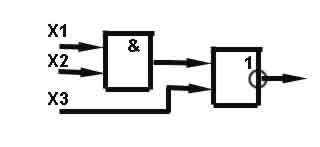
10. Нарисуйте логические схемы для следующих логических выражений и составьте ТИ.

Ответы:

№ вопроса

1

3

4

ответ

4*8*64*1024*1024=2147483648

4

3

«Решение логических задач». (4 балла)

1. Аськин, Баськин и Васькин стали свидетелями ограбления банка. Во время расследования Аськин сказал, что взломщики приехали на синей «Тойоте». Баськин считает, что это был красный «BMW», а Васькин утверждает, что это был «Форд-Фокус», но не синий. Выяснилось, что каждый из них назвал неправильно либо марку, либо цвет машины. На каком автомобиле приехали преступники?

2. В спортивных соревнованиях принимали участие пять команд: "Вымпел", "Метеор", "Нептун", "Старт" и "Чайка". Об их итогах соревнования имеется пять высказываний:
   1) Второе место занял "Вымпел", a "Cтарт" оказался на третьем.
   2) Хорошо выступала команда "Нептун", она стала победителем, а "Чайка" вышла на второе место.
   3) Да нет же, "Чайка" заняла только третье место, а "Нептун"- был последним.
   4) Первое место по праву завоевал "Cтарт", а "Метеор" был 4-м.
   5) Да, "Метеор", действительно, был четвертым, а "Вымпел" был 2-м.
   Известно, что команды не делили места между собой и что в каждом высказывании одно утверждение правильное, а другое нет.
   Как распределились места между командами?

3. Три школьника: Миша, Коля, Сергей, остававшихся в классе на перемене, были вызваны к директору по поводу разбитого в это время олна в кабинете. На вопрос директора о том, кто это сделал, мальчики ответили следующее:

Миша: «Я не бил окно и Коля тоже…» Коля: «Миша не разбивал окно, это Сергей разбил футбольным мячом!»

Сергей: «Я не делал этого, стекло разбил Миша.»

Выяснилось, что один из ребят сказал чистую правду, второй в одной части заявления соврал, а в другой сказал правду, третий соврал оба раза. Кто разбил стекло?

4. В финале турнира Российской армии по шахматам встретились представители шести воинских званий: майор, капитан, лейтенант, старшина, сержант и ефрейтор, разных специальностей: летчик, танкист, артиллерист, минометчик, сапер и связист. Определите специальность и звание каждого из шахматистов по следующим данным:

1) в первом туре лейтенант выиграл у летчика, майор - у танкиста, а сержант - у минометчика;

2) во втором туре капитан выиграл у танкиста;

3) в третьем и четвертом турах минометчик из-за болезни не участвовал в турнире, поэтому свободными от игры оказались капитан и ефрейтор;

4) в четвертом туре майор выиграл у связиста;

5) победителями турнира оказались лейтенант и майор, а хуже всех выступил сапер.

5. Три дочери писательницы Дорис Кей - Джуди, Айрис и Линда - тоже очень талантливы. Они приобрели известность в разных видах искусств - пении, балете и кино. Все они живут в разных городах, поэтому Дорис часто звонит им в Париж, Рим и Чикаго. Известно, что:

1) Джуди живет не в Париже, а Линда - не в Риме;

2) парижанка не снимается в кино;

3) та, кто живет в Риме, - певица;

4) Линда равнодушна к балету.

Где живет Айрис и какова ее профессия?

6. На одной улице стоят в ряд 4 дома, в каждом из которых живёт по одному человеку. Их зовут Алексей, Егор, Виктор, Михаил. Известно, что все они имеют разные профессии: рыбак, пчеловод, фермер, ветеринар. Известно, что: Фермер живёт правее пчеловода, Рыбак живёт правее фермера, Ветеринар живёт рядом с рыбаком, Рыбак живёт через дом от пчеловода, Алексей живёт правее фермера, Виктор - не пчеловод, Егор живёт рядом с рыбаком, Виктор живёт правее Алексея. Определите кто где живёт.

7. Маша, Оля, Лена и Валя -- замечательные девочки. Каждая из них играет на каком-нибудь музыкальном инструменте и говорит на одном из иностранных языков, инструменты и языки у них разные. Маша играет на рояле. Девочка, которая говорит по-французски, играет на скрипке. Оля играет на виолончели, а Лена не говорит по-немецки. Маша не знает итальянского языка, а Оля не владеет английским. Валя не знает французского, Лена не играет на арфе, а виолончелистка не говорит по-итальянски. Определите, кто на каком инструменте играет и на каком языке говорит.

8. В состав экспедиции входят Михаил, Сергей и Виктор. На обсуждении распределения обязанностей с руководителем проекта были высказаны предположения, что командиром будет назначен Михаил, сергей не будет механиком, а Виктор будет утверждён радистом, но командиром не будет. Позже выяснилось, что только одно из этих утверждений оказалось верным. Как распределились должности?

9. Перед началом Турнира Четырех болельщики высказали следующие предположения по поводу своих кумиров:

А) Макс победит, Билл - второй;

В) Билл - третий, Ник - первый;

С) Макс - последний, а первый - Джон.

Когда соревнования закончились, оказалось, что каждый из болельщиков был прав только в одном из своих прогнозов.

Какое место на турнире заняли Джон, Ник, Билл, Макс?

(В ответе перечислите подряд без пробелов места участников в указанном порядке имен.)

10. Классный руководитель пожаловался директору, что у него в классе появилась компания из 3-х учеников, один из которых всегда говорит правду, другой всегда лжет, а третий говорит через раз то ложь, то правду. Директор знает, что их зовут Коля, Саша и Миша, но не знает, кто из них правдив, а кто - нет. Однажды все трое прогуляли урок астрономии. Директор знает, что никогда раньше никто из них не прогуливал астрономию. Он вызвал всех троих в кабинет и поговорил с мальчиками. Коля сказал: "Я всегда прогуливаю астрономию. Не верьте тому, что скажет Саша". Саша сказал: "Это был мой первый прогул этого предмета". Миша сказал: "Все, что говорит Коля, - правда". Директор понял, кто из них кто. Расположите первые буквы имен мальчиков в порядке: "говорит всегда правду", "всегда лжет", "говорит правду через раз". (Пример: если бы имена мальчиков были Рома, Толя и Вася, ответ мог бы быть: РТВ)

Ответы:

№ вопроса

1

2

3

4

5

6

7

8

9

10

ответ

Красная «Тойота»

В,Ч,С,М,Н

Миша

Майор артиллерист, капитан лётчик, лейтенант связист, старшина миномётчик, сержант сапёр, ефрейтор танкист.

Айрис балерина, Париж

Пчеловод Михаил, фермер Егор, рыбак Алексей, ветеринар Виктор.

Ьаша - рояль, англ., Оля - виолончель, нем., Лена - скрипка, фр., Валя - арфа, ит.

Виктор командир, Михаил механик, Сергей радист.

3124

скм

Приложение 4. Бланк самооценивания

Насколько уверенно ты чувствуешь себя в следующих ситуациях?

Отметьте тот вариант, который вам больше подходит, знаком «1», остальные - «0»

НЕУВЕРЕННО

(2 балла)

ДОСТАТОЧНО

УВЕРЕННО (3 балла)

УВЕРЕННО

(4 балла)

ОЧЕНЬ УВЕРЕННО

(5 баллов)

Я могу составить таблицу истинности соответствующую логическому выражению.

Я могу упростить сложное логическое выражение используя законы алгебры логики.

Я могу построить логическую схему по заданной логической функции.

Я могу записать логическую функцию, реализуемую на выходе логической схемы.

Я могу решить логическую задачу на взаимно-однозначное сооветствие с помощью таблицы.

Я могу решить логическую задачу с помощью рассуждений.

Я могу решить логическую задачу методом используя построение логических выражений и деревьев.

Итого:

Подсчитайте количество баллов в каждом столбце. Вычислите результат: количество единиц в каждом столбце умножить на указанные баллы, сложить четыре суммы, результат разделить на 7.

Использованная литература:

1. Угринович Н.Д. Практикум по информатике и информационным технологиям. Учебное пособие для общеобразовательных учреждений / Н.Д. Угринович, Л.Л. Босова, Н.И. Михайлова. - М.: Бином. Лаборатория Знаний, 2002

2. Гейн А.Г. материалы курса «Математические основы информатики» - М.: Педагогический университет «Первое сентября», 2008

3. Методическая газета «Информатика» Издательский дом «Первое сентября» № 12 за 2010