Контрольная работа по информатике по теме Графы (в формате ОГЭ)

1 ВАРИАНТ

1. На ри­сун­ке - схема дорог, свя­зы­ва­ю­щих го­ро­да А, Б, В, Г, Д, Е, Ж и К. По каж­дой до­ро­ге можно дви­гать­ся толь­ко в одном на­прав­ле­нии, ука­зан­ном стрел­кой. Сколь­ко су­ще­ству­ет раз­лич­ных путей из го­ро­да А в город К?

П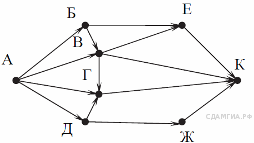

о­яс­не­ние.

Нач­нем счи­тать ко­ли­че­ство путей с конца марш­ру­та - с го­ро­да К. Пусть N_X - ко­ли­че­ство раз­лич­ных путей из го­ро­да А в город X, N - общее число путей.

В К можно при­е­хать из Е, В, Г или Ж, по­это­му N = N_К = N_Е + N_В + N_Г + N_Ж (*).

Ана­ло­гич­но:

N_Е = N_Б + N_В = 1 + 2 = 3;

N_В = N_А + N_Б = 1 + 1 = 2;

N_Ж = N_Д = 1;

N_Б = N_А = 1;

N_Г = N_А + N_В +N_Д = 1 + 2 + 1 = 4;

N_Д = N_А = 1.

Под­ста­вим в фор­му­лу (*): N = 3 + 2 + 4 + 1 = 10.

2) На ри­сун­ке изоб­ра­же­на схема дорог, свя­зы­ва­ю­щих го­ро­да A, B, C, D, E, F, G. По каж­дой до­ро­ге можно дви­гать­ся толь­ко в одном на­прав­ле­нии, ука­зан­ном стрел­кой. Сколь­ко су­ще­ству­ет раз­лич­ных путей из го­ро­да A в город D?

П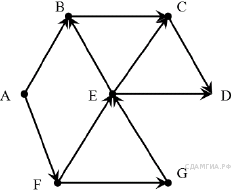

о­яс­не­ние.

Нач­нем счи­тать ко­ли­че­ство путей с конца марш­ру­та - с го­ро­да D. Пусть N_X - ко­ли­че­ство раз­лич­ных путей из го­ро­да А в город X, N - общее число путей.

В D можно при­е­хать из C или E, по­это­му N = N_D = N_C + N_E(*).

Ана­ло­гич­но:

N_C = N_B + N_E = 3 + 2 = 5;

N_B = N_A + N_E = 1 + 2 = 3;

N_E = N_F + N_G = 1 + 1 = 2;

N_G = N_F = 1;

N_F = N_А = 1.

Под­ста­вим в фор­му­лу (*): N = 5 + 2 = 7.

Ответ: 7.

3) Це­поч­ка из четырёх бусин, по­ме­чен­ных ла­тин­ски­ми бук­ва­ми, фор­ми­ру­ет­ся по сле­ду­ю­ще­му пра­ви­лу:

- на тре­тьем месте це­поч­ки стоит одна из бусин H, E;

- на вто­ром месте - одна из бусин D, E, C, ко­то­рой нет на тре­тьем месте;

- в на­ча­ле стоит одна из бусин D, H, B, ко­то­рой нет на вто­ром месте;

- в конце - одна из бусин D, E, C, не сто­я­щая на пер­вом месте.

Опре­де­ли­те, сколь­ко из пе­ре­чис­лен­ных це­по­чек со­зда­ны по этому пра­ви­лу?

DEHD HEHC DCEE DDHE DCHE HDHD BHED EDHC DEHE

В от­ве­те за­пи­ши­те толь­ко ко­ли­че­ство це­по­чек.

По­яс­не­ние.

Пер­вая це­поч­ка DEHD не удо­вле­тво­ря­ет четвёртому усло­вию пра­ви­ла, четвёртая DDHE - тре­тье­му. Седь­мая це­поч­ка BHED не удо­вле­тво­ря­ет вто­ро­му усло­вию пра­ви­ла. Вось­мая це­поч­ка EDHC не удо­вле­тво­ря­ет тре­тье­му усло­вию пра­ви­ла.

Таким об­ра­зом, имеем пять це­по­чек, удо­вле­тво­ря­ю­щих усло­вию.

Ответ: 5.