Учителю
Методическая разработка интегрированного урока математика-информатика 9 класс Построение и преобразование графиков квадратичной функции с помощью электронных таблиц функции

Методическая разработка интегрированного урока математика-информатика 9 класс Построение и преобразование графиков квадратичной функции с помощью электронных таблиц функции

Автор публикации: Агеева Н.В.

Дата публикации: 15.09.2016

Краткое описание:

предварительный просмотр материала

МЕТОДИЧЕСКАЯ РАЗРАБОТКА

ИНТЕГРИРОВАННОГО УРОКА

ИНФОРМАТИКИ И МАТЕМАТИКИ

Интегрированный урок "Построение и преобразование графиков квадратичной функции с помощью электронных таблиц" в 9 классе разработан в соответствии с ФГОС.

Разработка данного урока определяется новым пониманием стандарта общего образования, в котором основной акцент переносится с содержания на результаты образования. Поэтому в соответствии с содержанием программы и учебника по алгебре/информатике поставлена следующая дидактическая задача: формирование у обучающихся умений применения теоретических знаний о квадратичной функции в условиях получения опыта моделирования в Excel. Обучающиеся должны научиться использовать средства табличного процессора для построения, исследования, моделирования точечного графика, на примере, квадратичной функции.

Следует отметить, что информатика в данном уроке является интегратором, ведущей дисциплиной, а алгебра способствует уточнению материала. В информатике формируются многие виды деятельности, которые имеют метапредметный характер, способность к ним образует ИКТ-компетентность. Так на уроке с одной стороны обучающиеся используют различные способы задания функции - график, формула, таблица, с другой стороны - отрабатывают навыки правил записи формул и понимание принципа абсолютной и относительной адресации, табулирование функции, получение диаграмм (графиков). Табулирование функции - одна из часто решаемых прикладных задач математики. Табулирование означает построение таблицы значений функции для значений аргумента, изменяющихся в определенном интервале с данным шагом. Табулирование позволяет исследовать функцию: проследить характер изменения, выделить области корней, определить экстремальные значения.

Доминирующей формой обучения должна стать организация парной работы школьников или самостоятельное выполнение заданий, реализация которой осуществляется с помощью разноуровневых заданий. Электронная книга «Парабола» содержит 5 листов. Каждый лист представляет собой электронную таблицу и содержит шаблон для реализации математической модели функций вида y=kx², y=f(x+l), y=f(x)+m, y=f(x+l)+m, y=ax²+bx+c. Справа находится задание для обучающихся. Планируя урок в соответствии с индивидуальными и возрастными особенностями обучающихся, учитель может заранее изменить коэффициенты для функций в заданиях дифференцируя подход к сильным и слабым обучающимся.

Данный урок раскрывает определённые возможности для формирования универсальных учебных действий:

основа развития у обучающихся познавательных действий, в первую очередь логических и алгоритмических;
планирование (последовательности действий по решению задач);
систематизацию и структурирование знаний;
моделирование;
дифференциация существенных и несущественных условий;
формирование элементов системного мышления и приобретение основ информационной грамотности.

Тема урока: «Построение и преобразование графиков квадратичной функции с помощью электронных таблиц»

Цели урока:

I. Обучающие:

Закрепить умения получать графики функций видов y=kx², y=f(x+l), y=f(x)+m, y=f(x+l)+m, y=ax²+bx+c, если известен график функции y=f(x);
Отработать навыки получения точечных графиков с помощью графических средств табличного процессора.

II. Развивающие:

а) Формирование умений сравнивать, обобщать изучаемые факты;

b) Развивать информационную компетентность учащихся.

III. Воспитательные:

Воспитывать у учащихся активность и стремление познавать новое;
Воспитывать аккуратность выполнения работы, трудолюбие, упорства достижения цели.

Тип урока: интегрированный урок.

Знания, умения, навыки:

Знать алгоритм построения графиков функций видов y=kx², y=f(x+l), y=f(x)+m, y=f(x+l)+m, y=ax²+bx+c, если известен график функции y=f(x);;
Уметь получать графики с помощью графических средств табличного процессора.

Оборудование урока:

Интерактивная доска, проектор;
10 ЭВМ (ОС Windows, приложение Microsoft Excel);

Подготовка к уроку: На рабочем столе каждого компьютера поместить файл «Парабола».

Структура урока.

I. Организационный момент

2 мин

II. Ознакомление учащихся с новым материалом:

Подготовительная работа к изучению нового материала;
Сообщение темы и цели урока;
Формирование знания построения графиков в табличном процессоре

12 мин

1 мин

25 мин

III. Закрепление изученного на уроке:

Лист 1: y=kx²
Лист 2: y=(x+l)²
Лист 3: y=f(x)+m
Лист 4: y=f(x+l)+m
Лист 5: y=ax²+bx+c

7 мин

8 мин

IV. Постановка домашнего задания

1 мин

V. Подведение итогов

1 мин

ЗАПИСИ НА ДОСКЕ

ДЕЙСТВИЯ УЧИТЕЛЯ И УЧЕНИКОВ

РЕЧЬ УЧИТЕЛЯ И УЧЕНИКОВ

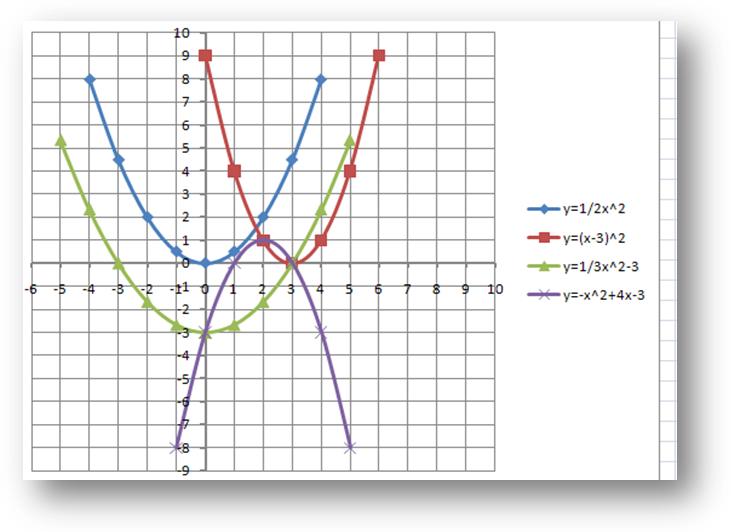
Методическая разработка интегрированного урока математика-информатика 9 класс Построение и преобразование графиков квадратичной функции с помощью электронных таблиц функции

1. у=1/2x²

2. y=(x-3) ²

3. y=1/3x² -3

4. y= - x² +4x-3Характеристика параболы

Параболы

Направление ветвей

Координаты вершины

Уравнение оси симметрии

Область определения

Дома: построить графики функций

y=2x²+4; y=2(x+3)²-5; y=(x-6)²; y= -(x-3)²+4

Учитель

Вопрос

Ответ

Установка

Учитель

Вопрос

Ответ

Учитель

Учитель объясняет выполнение практической работы

Вопрос

Ответ

Вопрос

Ответ

Учитель записывает результат в ячейку таблицы A3 и A7 соответственно

Учитель

Вопрос

Ответ

Учитель вносит начальное значение диапазона и формулу в соответствующие ячейки таблицы

Учитель

Вопрос

Ответ

Учитель записывает формулу

Вопрос

Ответ

Вопрос

Ответ

Учитель

Аналогично заполняю ячейки для другой функции

Учитель

Аналогично заполняем и строим графики функций

Установка

Учитель

Установка

I. ОРГАНИЗАЦИОННЫЙ МОМЕНТ

Задача: Организовать учащихся на урок

Здравствуйте, ребята! Садитесь все на свои места.

II. ОЗНАКОМЛЕНИЕ УЧАЩИХСЯ С НОВЫМ МАТЕРИАЛОМ

Задача: Познакомить учащихся с алгоритмом построения графика параболы при помощи графических средств табличного процессора

Подготовительная работа к изучению нового материала

Работаем устно.

Как называется линия, являющаяся графиком функции ?

Парабола

Посмотрите внимательно на доску.

На доске изображены параболы - графики квадратичных функций:

1. у=1/2 x²

2. y=(x-3) ²

3. y=1/3 x² -3

4. y= - x² +4x-3

Охарактеризуйте каждую из них.

1. у=1/2 x²

Направление ветвей - вверх

Уравнение оси симметрии x=0

Координаты вершины (0,0)

Область определения (-∞;+∞)

2. y=(x-3) ²

Направление ветвей - вверх

Уравнение оси симметрии x=3

Координаты вершины (3,0)

Область определения (-∞;+∞)

3. y=1/3x² -3

Направление ветвей - вверх

Уравнение оси симметрии x=0

Координаты вершины (0,-3)

Область определения (-∞;+∞)

4. y= - x² +4x-3

Направление ветвей - вниз

Уравнение оси симметрии x=2

Координаты вершины (2,1)

Область определения (-∞;+∞)

Молодцы!

Сообщение темы и цели урока

Сегодня на уроке мы научимся получать графики параболы с помощью табличного процессора MS Excel 2007.

3. Формирование знания построения графиков в табличном процессоре

Мы знаем, что компьютер - инструмент, который работает с конкретными математическими моделями. Рассмотрим математические модели квадратичной функции.

Открываем электронную таблицу Параболы, лист1.

Первая математическая модель парабола вида: y=kx²

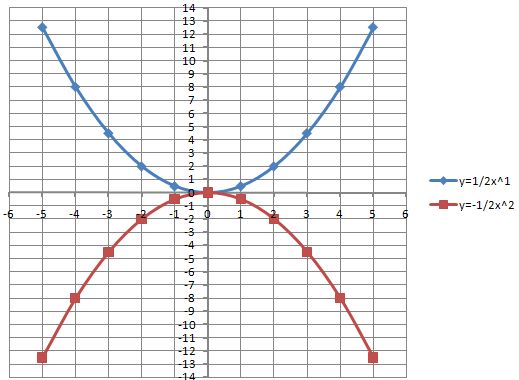
Задание: Построить графики функции у=1/2 x² и у = -1/2 x² в одной системе координат.

Для этого сначала укажем коэффициент k для первой и второй функции.

Чему равен коэффициент k для функции у=1/2 x² ?

1/2

Чему равен k для функции у= -1/2 x² ?

-1/2

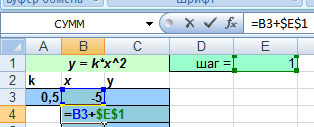
Теперь нужно указать диапазон значений для x. Для этого введем в ячейку для Х любое начальное значение диапазона.

Пусть начальным значением будет, например, число -5.

Как задать диапазон ячеек изменяющих значение с шагом 1?

Задать формулу заморозив значение шага, используя абсолютную адресацию.

А теперь дублируем формулу с помощью черного крестика в нижнем правом углу. Так как парабола симметрична относительно оси ОY, то дублируем до тех пор пока конечное значение функции не станет = начальному значению функции. Это нужно для того, чтобы точки были симметричны относительно оси ОY.

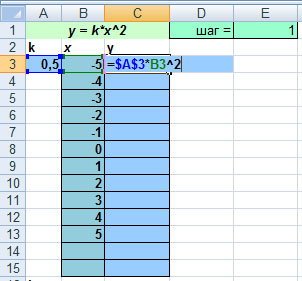
Затем нужно ввести формулу в ячейку для Y.

Как записать математическую модель параболы y=kx² в виде формулы в Excel ?

=$A$3*B3^2

Какие значения остаются неизменными?

Что тогда нужно сделать с этой ячейкой?

Заморозить.

Теперь дублируем эту формулу.

Аналогично выполняем для функции у = -1/2 x²

Для построения графика данных функций выбираем ВСТАВКА - ГРАФИК ТОЧЕЧНЫЙ-С ГЛАДКИМИ КРИВЫМИ и МАРКЕРАМИ.

Затем ВЫБРАТЬ ДАННЫЕ - ДОБАВИТЬ - указать название ряда, диапазон значений для Х и диапазон значений для Y - ОК. Затем снова добавить и применить уже к значениям второй функции.

Теперь рассмотрим вторую математическую модель: y=f(x+l) на примере квадратичной функции.

Итак, мы с вами рассмотрели построение графиков двух математических моделей параболы, а сейчас закрепим полученные знания.

III. ЗАКРЕПЛЕНИЕ ИЗУЧЕННОГО НА УРОКЕ МАТЕРИАЛА

Задача: формировать у учащихся умение получать графики парабол с помощью графических средств табличного процессора.

Выполнить практическую работу.

Сейчас Вы садитесь за компьютеры по два человека и выполняете данную практическую работу.

Всего 5 математических моделей параболы.

На отметку «5» необходимо выполнить 5 заданий.

На отметку «4» - 3-4 задания.

На отметку «3» - 1-2 задания

IV. ПОСТАНОВКА ДОМАШНЕГО ЗАДАНИЯ

Задача: сообщить учащимся домашнее задание

Откройте дневники и запишите домашнее задание: построить графики функций: y=2x²+4; y=2(x+3)²-5; y=(x-6)²; y= -(x-3)²+4

V. ПОДВЕДЕНИЕ ИТОГОВ УРОКА

⇧

⇩

скачать материал