- Учителю
- УРОК СОРЕВНОВАНИЕ Предмет: «Основы микропроцессорной техники» Тема: «Системы счисления. Представление чисел в различных системах счисления
УРОК СОРЕВНОВАНИЕ Предмет: «Основы микропроцессорной техники» Тема: «Системы счисления. Представление чисел в различных системах счисления
Министерство Образования и науки Республики Казахстан
РГКП «Семипалатинский финансово-экономический колледж имени
Рымбека Байсеитова»
УРОК СОРЕВНОВАНИЕ
Предмет: «Основы микропроцессорной техники»
Тема: «Системы счисления. Представление чисел в различных системах счисления.»
2016-2017 учебный год
Технологическая карта (план) урока № 5
Дисциплина: Основы микропроцессорной техники
Раздел 2. Арифметические и логические основы цифровой техники Тема 2.1 Арифметические основы ВТ
Тема урока 5: Системы счисления. Представление чисел в различных системах счисления.
Тип урока: комбинированный
Вид урока: урок соревнованиеЦели урока
обучающая
Научить понятиям программных и аппаратных средств ПК
воспитательная
Воспитывать такие качества как аккуратность, чувство ответственнности, привитие интереса к изучаемому предмету, сознательное отношение к учебе.
развивающая
Развитие навыков самостоятельного учебного труда, интеллектуального мышления, умения анализировать, логический излагать свои мысли.
Межпредметные связиТема 2.1 Системы счисления и представления данных
Оборудование урокаМаксимов Н.В., Попов И.И. Архитектура ЭВМ и ВС
Дополнительная
Белов А.В. Самоучитель по микропроцессорной технике
Содержание урока
Элементы урока, учебные вопросы,
формы и методы обучения
Дополнения, изменения
1.
Организационный момент 2мин
-
Приветствие обучающихся
-
Проверка готовности учебной аудитории к учебным занятиям
-
Проверка готовности обучающихся к учебно-практической деятельности
-
Проверка отсутствующих, заполнение учебного журнала
- Постановка цели и хода урока
2.
Опрос и проверка домашнего задания 15 мин
-
этапы ЭВМ
2 Понятие архитектуры ЭВМ
3 Основные устройства ПК
3.
Объяснение новой темы:
Раздел 2. Арифметические и логические основы цифровой техники
Тема 2.1 Арифметические основы ВТ
Тема урока 5: Системы счисления. Представление чисел в различных системах счисления.
4.
Закрепление урока. 8мин
Конкурс №1
Конкурс №2
5.
Домашнее задание. 1 мин
11-12 стр
7.
Подведение итогов урока. 1 мин
Преподаватель____________Аубакирова М.Ж.
Раздел 2. Арифметические и логические основы цифровой техники
Тема 2.1 Арифметические основы ВТ
Тема урока 5: Системы счисления. Представление чисел в различных системах счисления.
Система счисления - это способ записи (представления) чисел. Что под этим подразумевается? Например, вы видите перед собой несколько деревьев. Ваша задача - их посчитать. Для этого можно - загибать пальцы, делать зарубки на камне (одно дерево - один палец\зарубка) или сопоставить 10 деревьям какой-нибудь предмет, например, камень, а единичному экземпляру - палочку и выкладывать их на землю по мере подсчета. В первом случае число представляется, как строка из загнутых пальцев или зарубок, во втором - композиция камней и палочек, где слева - камни, а справа - палочки
Таблица 1 - Представление чисел в различных системах исчисление (начало)
1) К примеру число 37 нужно перевести из десятичной системы в двоичную, то нужно его делить на два, а затем проверять остаток от деления. Если остаток нечетный, то в низу мы подписывает единицу и следующий цикл деления идет через четное число, если останок от деления четный, то пишим ноль. На конце обязательно должна получиться 1. А теперь полученный результат мы преобразуем в двоичный, причем число идет справа на лево.
Пошагово: 37 - это число нечетное, значит 1, затем 36/2 = 18. Число четное, значит0. 18/2 = 9 число нечетное, значит 1, затем 8/2 = 4. Число четное, зачит 0. 4/2 = 2, число четное значит 0, 2/2 = 1.
Итак, мы получили число. Не забудьте счет идет справа налево: 100101 - вот мы получили число в двоичной системе. А вообще это записывается в виде деления в столбик, как вы видите ниже на рисунке:
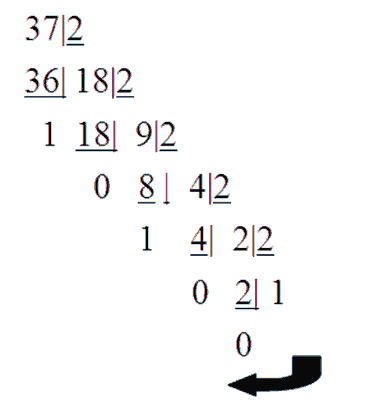
2) Но есть второй способ. Он мне больше нравиться. Перевод из одной системы в другую идет в следующем виде:
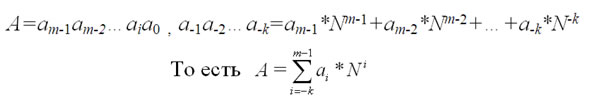
где ai - i-я цифра числа;
k - количество цифр в дробной части числа;
m - количество цифр в целой части числа;
N - основание системы исчисления.
Основание системы счисления N показывает, во сколько раз "вес" i-го разряда больше "веса" (i-1) разряда. Целая часть числа отделяется от дробной части точкой (запятой).
Целая часть числа AN1, с основой N1, переводится в систему счисления с основанием N2 путем последовательного деления целой части числа AN1 на записанную в виде числа с основанием N1 основу N2, до получения остатка.Полученная доля снова делится на основание N2, и этот процесс необходимо повторять, пока частица не станет меньше делителя. Полученные остатки от деления и последняя часть записываются в порядке, обратном полученном при делении. Сформированное число и будет целым числом с основанием N2.
Дробная часть числа AN1, с основой N1, переводится в систему счисления с основанием N2 путем последовательного умножения дробной части числа AN1 на основание N2, записанную в виде числа с основанием N1. При каждом умножении целая часть произведения берется в виде очередной цифры соответствующего разряда, а дробная часть оставшейся принимается за новую умножений. Число умножений определяет разрядность полученного результата, представляющий дробную часть числа AN1 в системе счисления N2. Дробная часть числа при переводе часто представляется неточно.
Давайте это сделаем на примере:
Перевод с десятичной в двоичную
37 в десятичной нужно перевести в двоичную. Давайте поработаем со степенями:
20 = 1
21 = 2
22 = 4
23 = 8
24 = 16
25 = 32
26 = 64
27 = 128
28 = 256
29 = 512
и так далее ... до бесконечности
Значит: 37 - 32 = 5. 5 - 4 = 1. Ответ следующий в двоичной системе: 100101.
Давайте переведем число 658 из десятичной в двоичную:
658-512=146
146-128=18
18-16=2. В двоичной системе число будет иметь вид: 1010010010.
Перевод с десятичной в восмеричную
Если вам надо перевести с десятичной в восьмеричную,
необходимо сначала перевести в двоичную, а затем с двоичной
перевести в восьмеричную. То есть так проще, хотя можно и сразу
перевести. По алгоритму подобному как в переводе в двоичную, см.
выше.
Перевод с десятичной в шестнадцатеричной
Если вам надо перевести с десятичной в шестнадцатеричную, необходимо сначала перевести в двоичную, а затем с двоичной перевести в шестнадцатеричную. То есть так проще, хотя можно и сразу перевести. По алгоритму подобному как в переводе в двоичную, см. выше.
Перевод с двоичной в восмеричную
Чтобы перевести число из двоичной в восьмиричную систему нужно двоичное разбить по три числа.
К примеру полученное число 1010010010 разбивает по три числа, причем разбивка идет справа налево: 1 010 010 010 = 1222. Смотрите таблицу в самом начале.
Перевод с двоичной в шестнадцатеричную
Чтобы перевести число из двоичной в шестнадцатеричное, надо разбить на тетрады (по четыре)
10 1001 0010 = 292
Привожу несколько примеров, для того, чтобы вы просмотрели:
Перевод осуществляется из двоичной в восьмиричную, затем в шестнадцатеричную, а затем из двоичной десятичную
(2) = 11101110
(8) = 11 101 110 = 276
(16) = 1110 1110 = EE
(10) = 1*128+ 1*64+ 1*32+ 0 +1*8 + 1*4 + 1*2+ 0= 238 3) (8) = 657
Перевод осуществляется из шестнадцатеричной в двоичную, затем в восьмиричную, а затем из двоичной десятичную
(16) = 6E8
(2) = 110 1110 1000
(8) = 11 011 101 000 = 2250
(10) = 1*1024+1*512+ 0 +1*128+ 1*64+ 1*32+ 8 = 1768
Преподаватель____________ Аубакирова М.Ж.
Конкурс 1
-
Расположите в порядке возрастания:
111010112; 1538; E36F16;198910.
-
Дана дата рождения в двоичной системе счисления: число
111102; месяц 1012; год 111110001012.Переведите все в
десятичную систему счисления и вы узнаете, когда я родилась?
3) Переведите все в двоичную систему счисления:
EF2716; 0,61238; 69910.
В восьмеричную систему счисления:
1110010100112; 1110000111002; 101100011,00002.
В шестнадцатеричную систему счисления:
0,10101110000111112; 111010000111,10110102;
1000100011112.
4) Сравните:
1138 и 11011002
5816 и 458
2888 и 105010
124510 и 1001112
20010и 15916
11111102и 7F16
5) В 10А и 10Б классах девочек 11102. Сколько мальчиков, если всего
1816 человек?
6) Вычислите:
3898+101112*C716-2458
1110111001112+11111111000112
11010012*1010102
11111000112-10000112
-
Выполните арифметические действия.
а) 20468+458 70658-3338
б) 105118+6768 3468-648
в) 5558+5558 7378-6268
г) 24CD116+AB16
д) 30116+F16
е) 5CFE16+C16
25CD16-3216
580EF16-D0216
102216-5A16
Конкурс №2
1) Переведите все числа в двоичную систему. Сложите верхние и нижние числа и из суммы нижних чисел, вычтите сумму верхних.
-
2) Переведите число 100000100101 из двоичной системы в десятичную и вы узнаете, когда школе будет 11001002 лет в десятеричной системе.
3) Равны ли числа и если нет, то какое больше.
7D516 и 110100011112
4) Решите пример:
(1010011112 - A716) / 258
5) Вычислите: 5A3C16 - 6E16 и 36768 - 6538 + AB16
6) Сравните:
A34F16 * 4658 и 5D7E16 - 10110102
Ответы:
-
1001001010 + 100111100 + 1000101110 = 10110110100 (Сумма верхних чисел).
10110001 + 110101000101 + 11110110 = 111011101100 (Сумма нижних чисел).
111011101100 - 10110110100 = 100100111000 (Ответ)
2) В 2085г. школе будет 100 лет
3) 2005 > 1679
4) 335 - 167 / 21 = 8
5) 59CE; 1384
6) 1260936310 > 215406010
1) 1538;111010112; 198910 E36F16;.
2) 3010. 0510.198910.
3) EF2716=11101111001001112
0,61238=0,1100010100112
69910=10101110112
1110010100112=71238
1110000111002=70348
101100011,100002=5438
0,10101110000111112=0,AE1F16
</ 111010000111,10110102=E87,5A16
1000100011112=88F16
4)
1138> 11011002
5816< 458
2888 < 105010
124510> 1001112
20010 >15916
11111102= 7F!6
5) Ответ: девочек 1410
всего: 2410
мальчиков: 1010
6) а) 3898=1000010012
C716=110001112
2458=101001012
101112*110001112=10001111000012
1000010012+10001111000012=100101111010102
100101111010102-101001012=100101010001012
б)1110111100112+11111111000112=101110110101102
в)11010012*1010102=10001001110102
г)11111000112-10000112=11101000002
7) а) 21138; 65328 е)5D0A16; FC8
б) 114078; 2628 ж)22128;4E04D416
в) 13328; 1118 з)13024228;E75A216
г) 24В7С16;259B16 и)1335628;181E6ACE16
д)31016; 573ED16
-