Разработка интегрированного урока по информатике (11 клас) и презентации к уроку

ТЕМА УРОКА:

«Ловись рыбка большая и маленькая»

(Вычисление площади криволинейной трапеции

методами приближенного вычисления в среде MS Excel.)

Задачи урока:

Образовательные:

1. Совершенствовать навыки работы в среде MS Excel.

2. Углублять и систематизировать знания работы с Мастером диаграмм.

Развивающие:

1. Способствовать развитию мышления, умения применять полученные знания при решении задач различной направленности.

2. Способствовать развитию представлений учащихся о прикладном значении программ MS-Office.

Воспитательные:

1. Воспитывать ответственность, коллективизм, взаимопомощь.

2. Воспитывать познавательный интерес к предмету.

Тип урока: Урок совершенствование знаний, умений и навыков в среде табличного процессора на основе полученных знаний в курсе «Алгебра и начала анализа».

Материально техническое оснащение:

1. Компьютеры с операционной системой Windows'98, Windows XP.

2. Программное обеспечение Microsoft Office: Excel 2003.

3. Мультимедийный проэктор. Экран.

4. Листы с ходом выполнения практического задания на компьютере

5. Листы с вопросами по домашнему заданию

Ход урока

Организационный момент.

Тема сегодняшнего урока: «Ловись рыбка большая и маленькая»

На предыдущих уроках мы изучили функции ЭТ, составляли таблицы, строили диаграммы. Сегодня на уроке, используя возможности ЭТ, мы рассмотрим три метода приближенного вычисления площади криволинейной трапеции:

• метод прямоугольников с недостатком;

• метод прямоугольников с избытком;

• метод трапеций.

Наша цель не дублирование и не повторение пройденной темы по алгебре, а углубление понятий, связанных с интегральным исчислением.

Вспомним немного истории: (показ презентаций учениками 11-а класса Фетько Дарьи и Полторак Анны.)

интегральное исчисление было предложено в 17 в. И.Ньютоном и

Г. Лейбницем. Интегрирование - нахождение интеграла, через который выражаются площади плоских фигур, длины кривых, объемы и поверхности тел и т.д.

Сам знак ∫ возник из первой буквы S латинского слова Summa. Но ведь при Евдоксе и Архимеде (400 г до н.э.) не было интегралов. Как же находили площади нестандартных фигур?

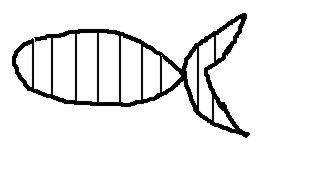
- Представим себе, что мы рыболовы …

- Как найти площадь пойманной рыбы?

Демонстрируются рисунки через проектор на экран

(рис1.)

Возможные ответы учащихся …

Учитель: Я предлагаю вам следующее. Разделим рыбу на несколько равных частей

(рис2.)

Введем систему координат (рис3.)

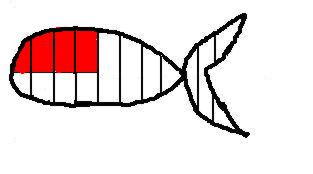
Посмотрим на закрашенную фигуру. Что она нам напоминает?

- отдаленно криволинейную трапецию.

Вопрос классу: Давайте вспомним: Что называют криволинейной трапецией?

Криволинейной трапецией называется фигура, ограниченная отрезком [a; b], графиком непрерывной функции не изменяющая своего знака на заданном отрезке и прямыми х=а и x=b.

(на доске через проектор)

У У У У

у=f(x) у=f(x)

a b Х

y=f(x)

a 0 b Х y=f(x)

0 a b Х a 0 b Х

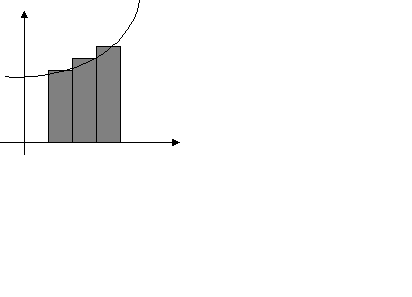
Вычислим площадь криволинейной трапеции приближенными способами.

1. Метод прямоугольников

с недостатком с избытком

Y Y

f(x_n) y=f(x) f(x_n) y=f(x)

f(x₀) f(x₀)

S1 S1

dx dx

0 х₀ х_nX 0 х₀ х_nX

dx - шаг разбиения

х₀ + dx = х₁f(x₀) - значение функции в точке х₀

…

x_n-1 + dx = x_nf(x_n) - значение функции в точке x_n

S1пр = F(x₀) * dx _{n-1 n}

S2пр = F(x₁) * dx S фигуры = Σ Si S фигуры = Σ Si

… (_{с недостатком) i=0 (c избытком) i=1}

Si пр = F(x_n-1) * dx

2. Метод трапеций Х y=f(x)

f(x_n)

S1трап = (F(x₀) + F(x₁)) / 2 * dx

S2трап = (F(x₁) + F(x₂)) / 2 * dx

… f(x₀)

Si трап = (F(x_n-1) + F(x_n)) / 2 * dx S

dx

_n 0 x₀ x_n Y

S фигуры = Σ Si

_{трапеции i=1}

Реализуем все методы через электронную таблицу.

Что нам необходимо знать?

1. Функцию

2. Пределы интегрирования

3. Шаг интегрирования (разбиения)

Рассмотрим на примере: 1. Функция Y= ,

ограниченная прямыми y = 0, x = 1, x = 2

2. Пределы интегрирования [1,2]

3. Шаг интегрирования dx = 0.1

Ресурсы ЭТ

1. Заголовочная часть.

2. Начальное и конечное значения аргумента (пределы интегрирования).

3. Шаг разбиения.

Заполним ЭТ в соответствии с тремя рассмотренными способами, при этом учтем следующее:

1. Вспомним, что обозначает «# # # # # #» при работе с формулами или с числами? (Не хватает места для записи чисел или формул, следовательно необходимо увеличить ширину колонки)

2. Можно ли заносить в одну ячейку числовую и текстовую информацию? (Нельзя)

3. Какую команду следует использовать для облегчения многократного ввода и идентичного вычисления данных? (Копирование)

4. Представление презентации проекта: «Анализ данных с помощью диаграмм» учеником 11 класса сш №45 Панасенко Иваном.

(Учитель показывает начало заполнения таблицы, далее вызывает контрольный пример и проводит объяснение с демонстрацией через проектор)

Замечание:

1. Особенности вычисления площади криволинейной трапеции методом прямоугольников с недостатком и с избытком.

Функция возрастающая Функция убывающая

YY

f(x_n) y=f(x) f(x_n) y=f(x)

f(x₀) f(x₀)

S1 S1

dx dx

0 х₀ х_nX 0 х₀ х_nX

_{n-1 n}

S фигуры = Σ Si S фигуры = Σ Si

(_{с недостатком) i=0 (c избытком) i=1}

При убывающей функции - формулы для вычисления соответствующих площадей криволинейных трапеций методом прямоугольников с недостатком и с избытком взаимо заменяются. (Почему?)

2. Поменяем шаг интегрирования с dx = 0,1 на dx = 0,5 следовательно изменится количество значений аргумента и соответствующих им значений функций, поэтому применяя команду копирования необходимо взять заведомо большее количество значений аргумента.

3. Рассмотрим графическое представление данной функции при различных dx.

Задание:

1. Найти площадь криволинейной трапеции, заданной функцией Y= всеми тремя способами. Сначала с шагом интегрирования dx = 0,1, а затем с шагом dx = 0,5.

2. Сравнить результаты вычислений, полученных при вычислении через электронную таблицу с найденным значением интеграл данной функции

= 0,5 кв. ед

Сравнив все полученные результаты, какой вывод можно сделать?

1. От чего зависит точность вычисления площади криволинейной трапеции?

2. Какой из способов дает более точное значение? Как вы думаете, почему?

Итак, подведем итог:

Точность вычисления площади криволинейной трапеции зависит:

1. От шага разбиения, т.е. шага интегрирования ( чем меньше шаг, тем больше точность вычисления)

2. От вида функции: монотонно-возрастающая или монотонно-убывающая.

3. От метода, применяемого к функции.

4. Наиболее точное значение вычисления площади криволинейной трапеции дает метод трапеций по отношению к точному результату

Посмотрим, справедлив ли этот вывод для других функций.

Задание классу: используя методы приближенного вычисления площади криволинейной трапеции, найти площади фигур с помощью MS Excel и сравнить их с точным значением интеграла. Полученные значения записать в тетрадь и сделать вывод.

Криволинейная трапеция ограничена графиком функции У = Х³ + 1 и прямыми У = 0, Х = 0, Х = 2

Домашнее задание: ( выдается на отдельных листочках каждому учащемуся)

Найти площадь криволинейной трапеции тремя различными способами и сравнить их с точным значением интеграла.

Криволинейная трапеция ограничена графиком функции У = 1/(Х + 2)² +1 и прямыми У = 0, Х = 0, Х = 2

Полученные значения записать в тетрадь и сделать вывод.