- Учителю
- Урок на тему 'ПРИБЛИЖЕННОЕ РЕШЕНИЕ СИСТЕМ УРАВНЕНИЙ'
Урок на тему 'ПРИБЛИЖЕННОЕ РЕШЕНИЕ СИСТЕМ УРАВНЕНИЙ'


 ПРИБЛИЖЕННОЕ РЕШЕНИЕ СИСТЕМ УРАВНЕНИЙ
ПРИБЛИЖЕННОЕ РЕШЕНИЕ СИСТЕМ УРАВНЕНИЙ
ИНТЕГРИРОВАННЫЙ УРОК ПО ИНФОРМАТИКЕ И МАТЕМАТИКЕ
ДЛЯ 9 КЛАССА
ЦЕЛИ: Систематизировать, расширить и углубить знания, умения учащихся по теме «Системы уравнений с двумя переменными», сформировать умения по решению систем уравнений графическим методом, применять их при построении и реализации на компьютере математических моделей для нахождения решений систем уравнений с разной степенью точности.
ЗАДАЧИ:
обучающие:
-
формирование умений интегрировать информацию (анализ и сравнение различных методов решения систем уравнений, обобщение);
-
формирование умений оценивать информацию (полезность и эффективность предложенных методов решения систем уравнений);
-
формирование умений адаптировать информацию к конкретным условиям (построение и исследование математических моделей, применение их к конкретным системам уравнений);
-
отработка умений и навыков работы в электронных таблицах (автозаполнение, работа с формулами, построение графиков функций).
развивающие:
-
освоение и сравнение предложенных методов решения;
-
умение применять данные методы при решении конкретных систем уравнений;
-
развитие памяти, внимания, наблюдательности, самостоятельности при работе на компьютере;
воспитательные:
-
формирование познавательного интереса путем описания математических объектов автоматическими средствами представления данных;
-
выработка у учащихся способности использовать компьютер при решении задач из различных предметных областей (математика);
-
прививать интерес к предмету через привлечение различных источников информации; расширять кругозор учащихся; способствовать формированию исследовательских и коммуникативных компетенций, навыков само- и взаимопроверки.
ТИП УРОКА: комбинированный.
ФОРМА УРОКА: интегрированный урок.
ОБОРУДОВАНИЕ:
-
Компьютеры с операционной системой Windows 7 и установленным пакетом Microsoft Office 2010, объединенные в локальную сеть
-
Интерактивная доска
-
Мультимедийный проектор
ХОД УРОКА
-
Организационный этап.
-
Актуализация знаний.
Учитель информатики: Ребята, мы продолжаем изучать тему: «Моделирование и формализация». Тема нашего урока: «Приближенное решение систем уравнений».
Сегодня мы поговорим о математических моделях. На языке математики формальные модели записываются с помощью уравнений. Точные решения существуют не для всех уравнений, поэтому для большинства уравнений приходится использовать приближенные решения с заданной точностью. Этим мы и займемся на уроке. Мы будем исследовать математические модели, соблюдая основные этапы моделирования.
Давайте их назовем.
Беседа с обучающимися. Обучающиеся называют этапы моделирования и дают характеристику каждому этапу. Слайд № 2
1 этап - Описательная информационная модель.
2 этап - Формализованная модель
3 этап - Компьютерная модель
4 этап - Компьютерный эксперимент
5 этап - Анализ полученных данных
Итак, мы начинаем с 1 этапа.
1 этап построения модели. Описательная информационная модель.
И я передаю слово учителю математики Елене Ивановне Андреевой.
Учитель математики:
Ребята, вы уже хорошо знакомы с решением систем уравнений с двумя переменными. Давайте вспомним теоретические сведения, которые понадобятся нам на уроке.
Слайд № 3. Фронтальный опрос:
1. Что называется системой уравнений?
2. Что называется решением системы уравнений с двумя неизвестными?
3. Что значит решить систему уравнений?
4. Назовите способы решения систем.
2 этап моделирования. Построение формализованной модели.
1. РЕШЕНИЕ СИСТЕМЫ УРАВНЕНИЙ
СПОСОБОМ ПОДСТАНОВКИ
Учитель математики: Ребята, давайте вспомним алгоритм решения систем уравнений с двумя переменными способом подстановки.
Алгоритм решения
-
Из какого-либо уравнения следует выразить, одну переменную через другую.
-
Подставить полученное выражение для переменной в другое уравнение и решить его.
-
Сделать подстановку найденного значения переменной и вычислить значение второй переменной.
Решить систему уравнений способом подстановки: x2 + 10 = y;
y - 30 = 2x.
x2 + 10 = y;
y - 30 = 2x,
y = x2 + 10;
x2 + 10 - 30 = 2x,
y = x2 + 10;
x2 - 2x - 20 = 0,
x2 - 2x - 20 = 0
D = b2 - 4ac
D= 84, D > 0, 2 корня
x1,2 = 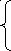
x1,2 = 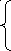
x1 =  x2 =
x2 = 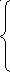
y1 = 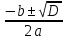 y2 =
y2 = 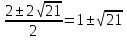
Ответ: 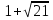 ,
, 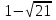
2. РЕШЕНИЕ СИСТЕМЫ УРАВНЕНИЙ
СПОСОБОМ СЛОЖЕНИЯ
Учитель математики: Ребята, давайте вспомним алгоритм решения систем уравнений с двумя переменными способом сложения.
Алгоритм решения
-
Следует уравнять модули коэффициентов при какой-нибудь переменной.
-
Складывая или вычитая полученные уравнения, найти одно неизвестное.
-
Подставить найденное значение в одно из исходных уравнений исходной системы, найти второе неизвестное.
Решить систему уравнений способом сложения: x2 + 10 = y;
y - 30 = 2x.
x2 + 10 = y;
y - 30 = 2x
x2 - y + 10 = 0;
-2x + y - 30 = 0,
y = x2 + 10;
x2 - 2x - 20 = 0,
x2 - 2x - 20 = 0
D = b2 - 4ac
D= 84, D > 0, 2 корня
x1,2 = 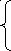
x1,2 = 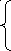
x1 =  x2 =
x2 = 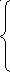
y1 = 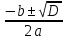 y2 =
y2 = 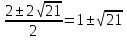
Ответ: 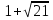 ,
, 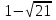
Учитель математики: Давайте проанализируем результат, полученный в первом и втором случае.
3. ГРАФИЧЕСКОЕ РЕШЕНИЕ
СИСТЕМЫ УРАВНЕНИЙ
Учитель математики: Ребята, давайте вспомним алгоритм решения систем уравнений с двумя переменными графическим способом.
Алгоритм решения
-
Выразить одну переменную через другую (например, у через х) в каждом уравнении.
-
Построить в одной системе координат график каждого уравнения.
-
Определить координаты точки пересечения.
-
Сделать проверку.
Решить систему уравнений графическим способом: x2 + 10 = y;
y - 30 = 2x.
Учитель математики: Ребята, как вы думаете, какой ответ у нас получится? Как в системе координат, изображённой в школьной тетради, определить значение абсцисс 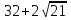 , и ординат
, и ординат 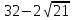
На этот вопрос вы найдёте ответ с помощью учителя информатики Марины Вячеславовны Матвейчук.
-
Объяснение нового материала.
Учитель информатики:
Приступаем к 3 этапу моделирования - Созданию компьютерной модели.
Графическое решение таких систем уравнений можно осуществить путем построения компьютерных моделей в электронных таблицах Microsoft Excel путем построения диаграмм типа «График».
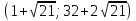
Решим систему уравнений на интервале [-10:10] с точностью 0,1.
Слайд № 10
Построим диаграмму - график первоначальной оценки решений
Слайд № 11
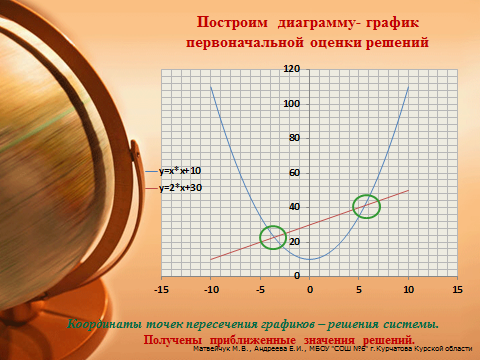
Координаты точек пересечения графиков - решения системы.
Получены приближенные значения решений.
Для уточнения значения решений теперь построим графики для интервалов
от -3 до -4,5, где находится первое решение, и от 5 до 7, где находится второе решение системы уравнений.
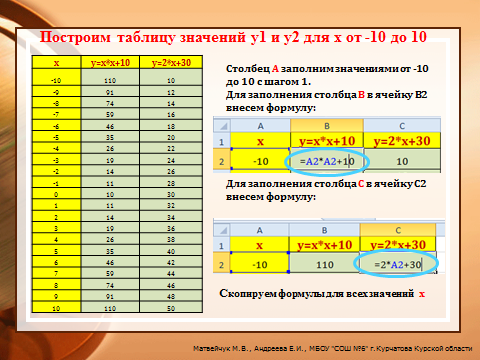
Составляем новую таблицу для х от -3 до 4,5.
Слайд № 13, 14
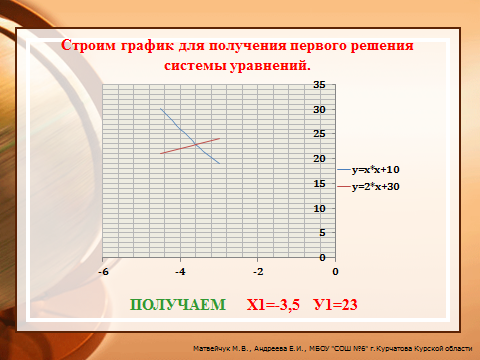
Получаем Х1=-3,5 У1=23
Составляем новую таблицу для х от 5 до 7
Слайд № 15, 16
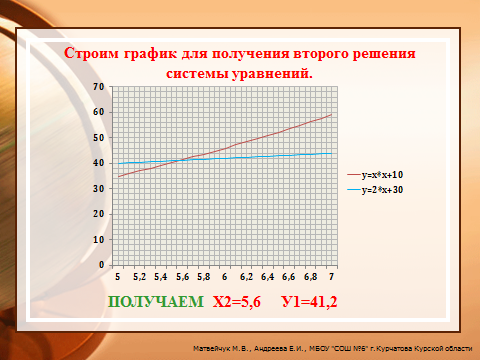
Получаем Х2=5,6 У1=41,2
Таким образом, решением нашей системы будут координаты точек пересечения графиков.
-
Отработка умений и навыков по созданию математических моделей на компьютере.
Переходим к 4 этапу моделирования - Компьютерному эксперименту.
Ребята, мы с вами рассмотрели графический способ решения системы уравнений. А сейчас вам предстоит самостоятельно реализовать данную математическую модель на компьютере. У каждого из Вас на рабочем столе располагается файл «Решение систем уравнений в Microsoft Excel» (Приложение). Вы можете к нему обратиться, если при выполнении задания возникнут трудности.
Работа на компьютере. Обучающиеся получают задания.
1 вариант
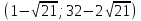
-
Решить систему уравнений методом сложения или методом подстановки.
-
Решить систему графическим методом средствами Microsoft Excel.
-
Сравнить полученные результаты.
2 вариант
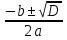
-
Решить систему уравнений методом сложения или методом подстановки.
-
Решить систему графическим методом средствами Microsoft Excel.
-
Сравнить полученные результаты.
5 этап моделирования. Анализ полученных результатов.
Беседа с обучающимися, выполнявшими задания 1 варианта, затем 2 варианта.
-
Кто из вас решал систему методом подстановки? Какой результат получили?
-
Кто из вас решал систему методом сложения? Какой результат получили?
-
Какой результат показал графический способ решения системы?
-
Какой же вывод можно сделать?
Ребята, вы совершенно правы. Каким бы способом не решалась система уравнений, ответ всегда получается один и тот же.
А какой способ выбрать - решает человек. Компьютер не может заменить человеческую мысль, но всегда помогает ее реализовать.
-
Рефлексия. Слайд № 18
Продолжи предложение
-
Сегодня на уроке я повторил…
-
Сегодня на уроке я закрепил…
-
Сегодня на уроке я поставил себе оценку …
-
Какие виды работ вызвали затруднения и требуют повторения…
-
В каких знаниях уверен…
-
Помог ли урок продвинуться в знаниях, умениях, навыках по предмету…
-
Кому, над, чем следовало бы ещё поработать…
-
Сегодня на уроке мне понравилось…
VI. Итог урока.
VII. Домашнее задание. Слайд № 19
Решить систему уравнений всеми известными вам способами.
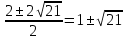
Построить математическую модель, соблюдая основные этапы моделирования. Составить алгоритм решения систем уравнений с двумя переменными путем построения компьютерных моделей в электронных таблицах Microsoft Excel
ПРИЛОЖЕНИЕ
(также можно использовать в качестве раздаточного материала)
Решение систем уравнений средствами Microsoft Excel
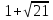 Решим систему уравнений
Решим систему уравнений
на интервале [-10:10] с точностью 0,1.
1 .

2. Построим диаграмму - график первоначальной оценки решений.
Для этого необходимо выделить всю таблицу, затем в меню «Вставка» выбрать «Диаграммы», тип «График».
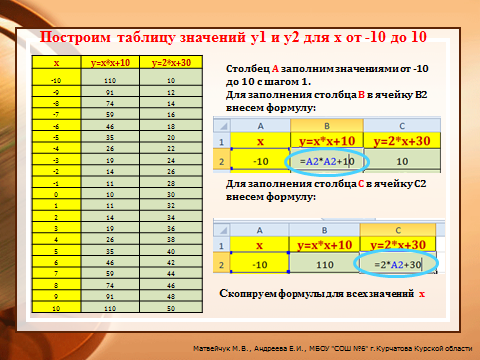
Получим:

Координаты точек пересечения графиков - решения системы.
Получены приближенные значения решений.
3. Для уточнения значения решений теперь построим графики для интервалов от -3 до -4,5, где находится первое решение,и от 5 до 7, где находится второе решение системы уравнений.
Составляем новую таблицу для х от -3 до 4,5.
x
y=x*x+10
y=2*x+30
-3
19
24
-3,1
19,61
23,8
-3,2
20,24
23,6
-3,3
20,89
23,4
-3,4
21,56
23,2
-3,5
22,25
23
-3,6
22,96
22,8
-3,7
23,69
22,6
-3,8
24,44
22,4
-3,9
25,21
22,2
-4
26
22
-4,1
26,81
21,8
-4,2
27,64
21,6
-4,3
28,49
21,4
-4,4
29,36
21,2
-4,5
30,25
21

Получаем Х1=-3,5 У1=23
Составляем новую таблицу для х от 5 до 7
x
y=x*x+10
y=2*x+30
5
35
40
5,1
36,01
40,2
5,2
37,04
40,4
5,3
38,09
40,6
5,4
39,16
40,8
5,5
40,25
41
5,6
41,36
41,2
5,7
42,49
41,4
5,8
43,64
41,6
5,9
44,81
41,8
6
46
42
6,1
47,21
42,2
6,2
48,44
42,4
6,3
49,69
42,6
6,4
50,96
42,8
6,5
52,25
43
6,6
53,56
43,2
6,7
54,89
43,4
6,8
56,24
43,6
6,9
57,61
43,8
7
59
44

Получаем Х2=5,6 У1=41,2
Таким образом, решением нашей системы будут координаты точек пересечения графиков.