Рабочая тетрадь по информатике на тему 'Основы логики' (9 класс)

РАБОЧАЯ ТЕТРАДЬ

По теме: ОСНОВЫ ЛОГИКИ

Учитель информатики МБОУ СОШ №15 Фатеева Н.И.

Г. Новочеркасск-2015

Основы логики

Логика - наука о формах и способах мышления.

Основные формы мышления:

• понятие

• суждение

• умозаключение.

Понятие - это форма мышления, фиксирующая основные, существенные признаки объекта.

Примеры:

Треугольник, горячий камень, компьютер

Высказывание- повествовательное предложение, в котором что-либо утверждается или отрицается: истина (False; 1) или ложь (True, 0).

Примеры:

А. Афины - столица Греции (истина)  А=1

В. Корова - хищное животное (ложь)  В=0

С. Сколько стоит? (не высказывание)

Умозаключение-это форма мышления ,с помощью которой из одного или нескольких суждений может быть получено новое суждение.

Пример:

Все углы равнобедренного треугольника равны. Отсюда можно заключить-Этот треугольник равносторонний.

Высказывания бывают простые и сложные(составные).

Алгебра высказываний служит для определения истинности или ложности составных высказываний.

Логическая переменная-простое высказывание, содержащее только одну мысль (обозначение-любая латинская буква A,B,C...Z).Значение логической переменной: «истина» (1) и «ложь» (0).

Логическая функция-составное высказывание,которое содержит несколько простых мыслей,соединённых между собой с помощью логических операций. Обозначение-F(A,B).

Операции над высказываниями

1. Отрицание (инверсия)

Инверсия делает истинное высказывание ложным и, наоборот.

Соответствует союзу НЕ

Обозначение Ā, ¬А, не А

А

А

0

1

1

0

2. Логическое умножение (коньюнкция)

Составное высказывание истинно только тогда, когда истины оба простых высказывания.

Соответствует союзу И

Обозначение & , ^,×

Х

Y

Z (X&Y)

1

1

1

1

0

0

0

1

0

0

0

0

Х= «6 делится на 2» = 1

Y= «6 делится на 3» = 1

Тогда Z=X&Y=1

3. Логическое сложение (дизъюнкция)

Составное высказывание истинно только тогда, когда истинно хотя бы одно из двух простых высказывания.

Соответствует союзу ИЛИ

Обозначение V,+

Х

Y

Z (X\/ Y)

1

1

1

1

0

1

0

1

1

0

0

0

Х= «6 делится на 2» = 1

Y= «18 - трехзначное число» = 0

Тогда Z=X Y=0

Пример 1:

Рассмотрим сложное высказывание. Представим данное высказывание в виде логической формулы.

Летом я поеду в деревню или в туристическую поездку.

Летом я поеду в деревню-обозначим А

Летом я поеду в туристическую поездку- обозначим В

Логическая формула-А\/ В

Пример 2:

Вычислить значение логической формулы:

Не А и В или А и Z,

если логические переменные имеют следующие значения:

А=ложь, В=истина,Z=истина.

Решение:

1.Отметим порядок действий

1) не А

2)не А и В

3) А и Z

4) Не А и В или А и Z

2.Вычислим по шагам

Не ложь=истина

Истина и истина=истина

Ложь и истина =ложь

Истина или ложь=истина

Ответ: истина

Упражнение 1.

1.Число 8 делиться на 4, и число 8 делиться на 2.

2.Неверно,что 4 делиться на 3.

Упражнение 2.

1.F=(0\/0) \/ (1\/ 1)

2.A и B или не B ,если А=ложь, В=истина

Упражнение 3.

Постройте сложное высказывание с помощью «И», «ИЛИ».

Андрей старше Светы. Наташа старше Светы.

Проверочное задание

Вариант 3

1.Какие из предложений являются высказываниями? Определите их истинность.

а)Все роботы являются машинами.

б)Чему равно расстояние от Земли до Марса?

2.Представить данное высказывание в виде логической формулы.

Если Маша- сестра Саши, то Саша -брат Маши.

3.Вычислить значение логической формулы:

F= ¬1&(1\/1) \/ (¬0&1)

4.Постройте сложное высказывание с помощью «И», «ИЛИ».

Часть детей - девочки.

Остальные - мальчики.

Вариант 4

1.Какие из предложений являются высказываниями? Определите их истинность.

а)Внимание!

б)Париж-столица Англии.

2.Представить данное высказывание в виде логической формулы.

Неверно, что корова- хищное животное.

3.Вычислить значение логической формулы:

F=(0&0) \/ ¬ (1&1)

4.Постройте сложное высказывание с помощью «И», «ИЛИ».

Одни дети- рисуют.

Другие дети -читают.

Таблицы истинности

Для логического выражения можно построить таблицу истинности, которая определяет его истинность или ложность при всех возможных комбинациях исходных значений простых высказываний.

Правило составления таблицы истинности.

1. Определить количество строк в таблице по формуле q=2ⁿ, где n - количество логических переменных.

2. Выяснить количество столбцов таблицы: количество логических переменных + количество логических операций.

3. Построить таблицу истинности, обозначить столбцы, внести всевозможные наборы исходных данных логических переменных.

4. Заполнить таблицу истинности, выполняя базовые логические операции в необходимой последовательности.

Пример:

Построить таблицу истинности для выражения:

1. Количество строк таблицы 2² = 4, т.к. в формуле две переменные A и B.

2. Количество столбцов: 2 переменные + 5 логических операций = 7.

A

B

A\/B

\/

F

⁰

⁰

⁰

¹

¹

¹

⁰

⁰

¹

¹

¹

⁰

¹

¹

¹

⁰

¹

⁰

¹

¹

¹

¹

¹

¹

⁰

⁰

⁰

⁰

Логические схемы

Правило построения логических схем.

1.Определить число логических переменных.

2.Определить количество базовых логических операций и их порядок.

3.Изобразить для каждой логической операции соответствующий ей логический элемент.

4.Соединить логические элементы в порядке возрастания логических операций.

Схематическое изображение логических операций.

конъюнкция

дизъюнкция

инверсия

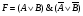
В этой таблице использованы следующие обозначения:

1-истина; 0-ложь;

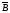
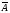
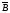-логические элементы (логические операции)

Пример 1:

1.Построить логическую схему для логического выражения и вычислить значения выражения для Х=1 ,Y=0

F=X&Y\/ (Y\/X)

Решение:

1.Переменных две X и Y

Карточки

Карточка 1

1.Построить логическую схему для логического выражения и вычислить значения выражения для А=1 ,В=0,С=1

Не А или В

2.Дана логическая схема. Построить логическое выражение, соответствующее этой схеме. Вычислить значение выражения для:

A=0, D=1

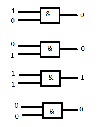
Карточка 2

1.Построить логическую схему для логического выражения и вычислить значения выражения для А=1 ,В=0,С=1

А или В и С

2.Дана логическая схема. Построить логическое выражение, соответствующее этой схеме. Вычислить значение выражения для:

A=1, D=0

Карточка 3.

1.Построить логическую схему для логического выражения и вычислить значения выражения для А=1 ,В=0,С=1

Не(А и В и С)

2.Дана логическая схема. Построить логическое выражение, соответствующее этой схеме. Вычислить значение выражения для:

A=1, D=1

Карточка 4.

1.Построить логическую схему для логического выражения и вычислить значения выражения для А=1 ,В=0,С=1

Не А или В и С

2.Дана логическая схема. Построить логическое выражение, соответствующее этой схеме. Вычислить значение выражения для:

A=0, D=0

Логические законы и тождества

Тождества

Логического сложения

1. А+0=А

2. А+1=1

3. А+А=А

4. А+ ¬ А=1

Логического умножения

1. А&0=0

2. A&1=A

3. A&A=A

4. A& ¬ A=0

Законы

• Переместительный закон

A+B=B+A A&B=B&A

• Сочетательный закон

(A+B)+C=A+(B+C) (A&B)&C=A&(B&C)

• Распределительный закон

(A+B)&C=A&C+B&C

A&B+C=(A+C)&(B+C)

1. X X (Х=Х) Закон тождества
2. Закон противоречия
3. Закон исключенного третьего
4. Закон двойного отрицания
5. X X X , X X  Законы идемпотентности
6        ,        Законы коммутативности (переместительности)
                ,                - Законы ассоциативности (сочетательности)
8.                   ,                    - Законы дистрибутивности (распределительности)
9. , Законы де Моргана

10.(A→B)=A&

Упражнения

Пример 1.

Пример 2.

Пример 3.

Логические операции- логическое действие.

Упражнение 1.

Какие из предложений являются высказываниями? Определите их истинность.
Земля - планета Солнечной системы.

Какого цвета этот дом?
1+8<5
5 · 4=20
Всякий квадрат есть параллелограмм.

Пейте яблочный сок!
Каждый параллелограмм есть квадрат.
3 · 2 =5
Стоп!

4.Логическое следование (импликация)

Импликация образуется соединением двух высказываний в одно с помощью оборота речи «если…, то…».

Импликация ложна только тогда, когда из истинного первого высказывания (предпосылки) следует ложный вывод (второе высказывание).

Обозначение А→В

A

B

A→B

0

0

1

0

1

1

1

0

0

1

1

1

5.Логическое равенство(эквивалентность)

Эквивалентность образуется соединением двух высказываний в одно с помощью оборота речи «… тогда и только тогда, когда …».

Обозначение A ≡ B, А~B

A

B

А~B

0

0

1

0

1

0

1

0

0

1

1

1

Логическое выражение - формула, в которую входят логические переменные и знаки логических операций.

Порядок выполнения логических операций:

1. Действия в скобках.

2. Инверсия, конъюнкция, дизъюнкция, импликация, эквивалентность.

Упражнение 4.

Составьте и запишите истинные сложные высказывания из простых с использованием логических операций:

1. Любое из чисел X, Y,Z отрицательно.

Проверочное задание

Вариант 1

1.Какие из предложений являются высказываниями? Определите их истинность.

А)Число 10- чётное.

Б)Всякий моряк умеет плавать.

2.Представить данное высказывание в виде логической формулы.

Число 15 нечётное и двузначное.

3.Вычислить значение логической формулы:

F=(1\/1) \/ (1\/ 0)

4.Постройте сложное высказывание с помощью «И», «ИЛИ».

Все ученики изучают информатику.

Все ученики изучают химию.

Вариант 2

1.Какие из предложений являются высказываниями? Определите их истинность.

А)Посмотрите на доску.

Б)Наполеон был немецким

императором.

2.Представить данное высказывание в виде логической формулы.

При замерзании воды выделяется тепло.

3.Вычислить значение логической формулы:

F=(0&0) \& (1&1)

4.Постройте сложное высказывание с помощью «И», «ИЛИ».

В кабинете есть учебники.

В кабинете есть справочники.

Упражнение 1

Составьте таблицу истинности для логического выражения:

F = (X & ¬Y) v Z

Упражнение 2

Заполните пустые ячейки таблицы истинности:

^A

^B

^¬B

^AvB

^¬(AvB)

^{¬B& ¬(AvB)}

¹

⁰

⁰

⁰

⁰

⁰

¹

¹

⁰

¹

⁰

¹

⁰

Упражнение 3

Запишите в виде логической формулы следующие высказывания:

1.Если Петров здоров и богат, то он здоров.

Упражнение 4

Используя связку «ЕСЛИ…,ТО…»,измените высказывание.

Например: Человек ,любящий животных,-добрый.

Если человек любит животных, то он -добрый.

1.В високосном году 366 дней.

2.Тише едешь -дальше будешь.

2.Логических операций- дизъюнкция, две конъюнкции, инверсия.

3.Схему строим слева направо в соответствии с порядком логических операций:

4.Вычислим значение выражения:

F=X&Y\/ (Y\/X)

F=1&0\/ (0\/1)=0 Ответ: 0

Пример 2:

Выполнить вычисления по логической схеме. Запишите соответствующее логическое выражение:

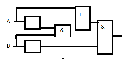
Ответ: F=A&B+(A+B)=1&0+(1+0)=1

Упражнение 1.

1.Построить логическую схему для логического выражения и вычислить значения выражения для А=0 ,В=1,С=1

F=^¬(A\/^B&^C)

^2. Выполнить вычисления по логической схеме. Запишите соответствующее логическое выражение:

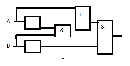
Проверочная работа

1 вариант

Составьте таблицу истинности для логического выражения:

F=(X&^¬Y) \/Z

Построить логическую схему для логического выражения

F=(X&^¬Y) \/Z

Составить логическое выражение по схеме:

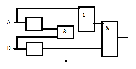
2 вариант

Составьте таблицу истинности для логического выражения:

F=^¬(X\/^Y)&(Y\/^X)

Построить логическую схему для логического выражения

F=^¬(X\/^Y)&(Y\/^X)

Составить логическое выражение по схеме:

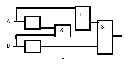
3 вариант

Составьте таблицу истинности для логического выражения:

F=A&B\/^¬B

Построить логическую схему для логического выражения

F=A&B\/^¬B

Составить логическое выражение по схеме:

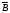
4 вариант

Составьте таблицу истинности для логического выражения:

F=A&B\/(^¬B \/^¬A)

Построить логическую схему для логического выражения

F=A&B\/(^¬B \/^¬A)

Составить логическое выражение по схеме: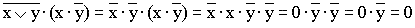

11.(A→B)=A

12. X 1  ,     
13.      ,     
14.          ,          Законы поглощения
15.             ,             Законы склеивания

16.A A)

Пример 1.

Упростить формулу (А+В)· (А+С)
Решение.
а) Раскроем скобки
( A + B ) · ( A + C )   ·    · C + B · A + B · C
б) По закону идемпотентности A · A   , следовательно,
 ·    · C + B · A + B · C     · C + B · A + B · C
в) В высказываниях А и А· C вынесем за скобки А и используя свойство А+1 1, получим
А+А· С  ·    · C   ·   С   ·    · С    ·   · С
г Аналогично пункту в) вынесем за скобки высказывание А.
   ·    · С         · С    · С
Таким образом, мы доказали закон дистрибутивности.

Пример 2. Упростить выражение А  · 
Решение.
   ·           - поглощение

Пример 3. Упростить выражение  ·    ·
Решение.
 ·    ·         - склеивание

Проверочная работа

1 вариант

Упростите выражения:

2 вариант

Упростите выражения: