Поурочные разработки курса информатики 11 класса

Логические основы построения компьютера

1. Понятие, суждение, умозаключение.

Первые учения о формах и способах рассуждений возникли в странах Древнего Востока (Китай, Индия), но в основе современной логики лежат учения, созданные в 4 веке до нашей эры древне-греческими мыслителями. Основы формальной логики заложил Аристотель, который впервые отделил логические формы речи от ее содержания. Он исследовал терминологию логики, подробно разобрал теорию умозаключений и доказательств, описал ряд логических операций, сформулировал основные законы мышления.

Логика изучает внутреннюю структуру процесса мышления, который реализуется в таких естественно сложившихся формах как понятие, суждение, умозаключение и доказательство.

Понятие. Понятие - это форма мышления, отражающая наиболее существенные свойства предмета, отличающие его от других предметов. В структуре каждого понятия нужно различать две стороны: содержание и объем. Содержание понятия составляет совокупность существенных признаков предмета. Чтобы раскрыть содержание понятия, следует выделить признаки, необходимые и достаточные для выделения данного предмета по отношению к другим предметам.

Объем понятия определяется совокупностью предметов, на которую оно распространяется, и может быть представлено в форме множества объектов, состоящего из элементов множества.

Алгебра множеств, одна из основополагающих современных математических теорий, позволяет исследовать отношения между множествами и, соответственно, объемами понятий.

Между множествами (объемами понятий) могут быть различные виды отношений:

• равнозначность, когда объемы понятий полностью совпадают;

• пересечение, когда объемы понятий частично совпадают;

• подчинения, когда объем одного понятия полностью входит в объем другого и т.д.

Для наглядной геометрической иллюстрации объемов понятий и соотношений между ними используются диаграммы Эйлера-Венна. Если имеются какие-либо понятия A, B, C и т.д., то объем каждого понятия (множество) можно представить в виде круга, а отношения между этими объемами (множествами) в виде пересекающихся кругов.

Высказывание. Высказывание (суждение) - это форма мышления, выраженная с помощью понятий, посредством которой что-либо утверждают или отрицают о предметах, их свойствах и отношениях между ними.

О предметах можно судить верно или неверно, т.е. высказывание может быть истинным или ложным. Истинным будет суждение, в котором связь понятий правильно отражает свойства и отношения реальных вещей. Ложным суждение будет в том случае, когда связь понятий искажает объективные отношения, не соответствует реальной действительности.

Обоснование истинности или ложности простых высказываний решается вне алгебры логики. Например, истинность или ложность высказывания: "Сумма углов треугольника равна 180 градусов" устанавливается геометрией, причем - в геометрии Евклида это высказывание является истинным, а в геометрии Лобачевского - ложным.

В естественном языке высказывания выражаются повествовательными предложениями. Высказывание не может быть выражено повелительным или вопросительным предложением, оценка истинности или ложности которых невозможна. Высказывания могут выражаться с помощью математических, физических, химических и прочих знаков. Из двух числовых выражений можно составить высказывания, соединив их знаками равенства или неравенства.

Высказывание называется простым, если никакая его часть сама не является высказыванием. Высказывание, состоящее из простых высказываний, называются составным (сложным).

Высказывания имеют определенную логическую форму. Понятие о предмете мысли называется субъектом и обозначается буквой S, а понятие о свойствах и отношениях предмета мысли называется предикатом и обозначается буквой P. Оба эти понятия - субъект и предикат называются терминами суждения. Отношения между субъектом и предикатом выражается связкой «есть», «не есть», «является», «состоит» и т.д.

Таким образом, каждое высказывание состоит из трех элементов - субъекта, предиката и связки (двух терминов и связки). Состав суждения можно выразить общей формулой «S есть "» или «S не есть P».

Умозаключение. Умозаключение - это форма мышления, посредством которой из одного или нескольких суждений, называемых посылками, по определенным правилам логического вывода получается новое знание о предметах реального мира (вывод).

Умозаключения бывают дедуктивные, индуктивные и по аналогии. В дедуктивных умозаключениях рассуждения ведутся от общего к частному. Например, из двух суждений: «Все металлы электропроводны» и «Ртуть является металлом» путем умозаключения можно сделать вывод, что: «Ртуть электропроводна».

В индуктивных умозаключениях рассуждения ведутся от частного к общему. Например, установив, что отдельные металлы - железо, медь, цинк, алюминий и т.д. - обладают свойством электропроводности, можно сделать вывод, что все металлы электропроводны.

Умозаключение по аналогии представляет собой движение мысли от общности одних свойств и отношений у сравниваемых предметов или процессов к общности других свойств и отношений. Например, химический состав Солнца и Земли сходен по многим показателям, поэтому, когда на Солнце обнаружили неизвестный еще на Земле химический элемент гелий, то по аналогии заключили: такой элемент есть и на Земле.

Пример 1.

Истинные высказывания: а) "2+2=4"; б) "сила притяжения тел обратно пропорциональна квадрату расстояния между ними" в) "зайцы питаются растениями"; г) "бит - фундаментальная единица информации, используемая в теории информации"; д) "два треугольника равны, если две стороны и угол между ними одного треугольника равны двум сторонам и углу между ними другого треугольника"; е) "понедельник - первый день недели".

Ложные высказывания: а) "4+3=5"; б) "тело падает на Землю с ускорением, пропорциональным своей массе"; в) "животные это неживая природа" г) "информатика - наука о термической обработке металлов"; д) "квадрат это фигура у которой пять сторон"; е) "лев - домашнее животное".

Пример 2.

а) "Эльбрус - не высочайшая горная вершина Европы"; б) "2<5"; в) "10>=7"; г) "не все натуральные числа целые"; д) "не через любые три точки на плоскости можно провести окружность"; е) "теннисист Кафельников проиграл финальную игру"; ж) "мишень не поражена первым выстрелом"; з) "это утро не ясное или оно не теплое" (Пояснение. Пусть А = "это утро ясное", а B = "это утро теплое". Тогда "это утро ясное и теплое" можно записать как А•В, отрицанием чего является , что соответствует высказывательной форме "это утро не ясное или оно не не теплое"; и)"число n не делится на 2 и оно делится на 3"; к) "этот треугольник не равнобедренный или он не прямоугольный"; л) "не каждый ученик писал контрольную своей ручкой" (вариант: "кто-то писал контрольную не своей ручкой").

Пример 3. Определите, какие из высказываний (высказывательных форм) в следующих парах являются отрицаниями друг друга, а какие нет:

• а) "5<10", "5>10";

• б) "10>9", "10<=9";

• в) "мишень поражена первым выстрелом", "мишень поражена вторым выстрелом";

• г) "машина останавливалась у каждого из двух светофоров", "машина не останавливалась у каждого из двух светофоров",

• д) "человечеству известны все планеты Солнечной системы", "в Солнечной системе есть планеты, неизвестные человечеству";

• е) "существуют белые слоны", "все слоны серые";

• ж) "кит - млекопитающее", "кит - рыба";

• з) "неверно, что точка А не лежит на прямой а", "точка А лежит на прямой а";

• и) "прямая а параллельна прямой b", "прямая a перпендикулярна прямой b";

• к) "этот треугольник равнобедренный и прямоугольный", "этот треугольник не равнобедренный или он не прямоугольный".

: Являются отрицаниями друг друга: б), г), д), к);
не являются отрицаниями друг друга: а), в), е), ж), з), и).

Пример 4.

• а) "наличия аттестата о среднем образовании достаточно для поступления в институт";

• б) "наличие аттестата о среднем образовании необходимо для поступления в институт";

• в) "если целое число делится на 6, то оно делится на 3";

• г) "подобие треугольников является необходимым условием их равенства";

• д) "подобие треугольников является необходимым и достаточным условием их равенства";

• е) "треугольники подобны только в случае их равенства";

• ж) "треугольники равны только в случае их подобия";

• з) "равенство треугольников является достаточным условием их подобия";

• и) "для того, чтобы треугольники были неравны, достаточно, чтобы они были неподобны";

• к) "для того, чтобы четырёхугольник был квадратом, достаточно, чтобы его диагонали были равны и перпендикулярны".

: Истинны: б), в), г), з), к), и);
ложны: а), д), е), ж).

2. Операции конъюнкции, дизъюнкции и отрицания.

Алгебра в широком смысле этого слова наука об общих операциях, аналогичных сложению и умножению, которые могут выполняться над различными математическими объектами (алгебра переменных и функций, алгебра векторов, алгебра множеств и т.д.). Объектами алгебры логики являются высказывания.

Алгебра логики отвлекается от смысловой содержательности высказываний. Ее интересует только один факт - истинно или ложно данное высказывание, что дает возможность определять истинность или ложность составных высказываний алгебраическими методами.

Простые высказывания в алгебре логики обозначаются заглавными латинскими буквами:

А = {Аристотель - основоположник логики}

В = {На яблонях растут бананы}.

Истинному высказыванию ставится в соответствие 1, ложному - 0. Таким образом, А = 1, В = 0.

Составные высказывания на естественном языке образуются с помощью союзов, которые в алгебре высказываний заменяются на логические операции. Логические операции задаются таблицами истинности и могут быть графически проиллюстрированы с помощью диаграмм Эйлера-Венна.

Логическая операция КОНЪЮНКЦИЯ (логическое умножение):

 в естественном языке соответствует союзу и;

 в алгебре высказываний обозначение (& );

 в языках программирования обозначение And.

Конъюнкция - это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания истинны.

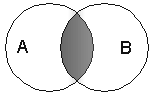
В алгебре множеств конъюнкции соответствует операция пересечения множеств, т.е. множеству получившемуся в результате умножения множеств А и В соответствует множество, состоящее из элементов, принадлежащих одновременно двум множествам.

Таблица истинности Диаграмма Эйлера-Венна

А В А и В

0 0 0

0 1 0

1 0 0

1 1 1

Логическая операция ДИЗЪЮНКЦИЯ (логическое сложение):

 в естественном языке соответствует союзу или;

 обозначение v ;

 в языках программирования обозначение Or.

Дизъюнкция - это логическая операция, которая каждым двум простым высказываниям ставит в соответствие составное высказывание, являющееся ложным тогда и только тогда, когда оба исходных высказывания ложны и истинным, когда хотя бы одно из двух образующих его высказываний истинно.

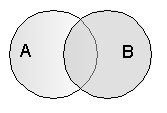
В алгебре множеств дизъюнкции соответствует операция объединения множеств, т.е. множеству получившемуся в результате сложения множеств А и В соответствует множество, состоящее из элементов, принадлежащих либо множеству А, либо множеству В.

Таблица истинности Диаграмма Эйлера-Венна

А В А или В

0 0 0

0 1 1

1 0 1

1 1 1

Логическая операция ИНВЕРСИЯ (отрицание):

 в естественном языке соответствует словам неверно, что... и частице не;

 обозначение ;

 в языках программирования обозначение Not;

Отрицание - это логическая операция, которая каждому простому высказыванию ставит в соответствие составное высказывание, заключающееся в том, что исходное высказывание отрицается.

В алгебре множеств логическому отрицанию соответствует операция дополнения до универсального множества, т.е. множеству получившемуся в результате отрицания множества А соответствует множество , дополняющее его до универсального множества.

Таблица истинности Диаграмма Эйлера-Венна

A _{не А}

0 1

1 0

3. Операции импликации и эквиваленции.

Логическая операция ИМПЛИКАЦИЯ (логическое следование):

 в естественном языке соответствует обороту если ..., то ...;

 обозначение →.

Импликация - это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся ложным тогда и только тогда, когда условие (первое высказывание) истинно, а следствие (второе высказывание) ложно.

А В А→В

0 0 1

0 1 1

1 0 0

1 1 1

Логическая операция ЭКВИВАЛЕНЦИЯ (равнозначность):

 в естественном языке соответствует оборотам речи тогда и только тогда; в том и только в том случае;

 обозначения ~.

Эквиваленция - это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания одновременно истинны или одновременно ложны. Таблица истинности эквиваленции:

А В А ~ В

0 0 1

0 1 0

1 0 0

1 1 1

Практическая часть.

Пример 1. Формализуйте предостережение, которое одна жительница древних Афин сделала своему сыну, собиравшемуся заняться политической деятельностью: "Если ты будешь говорить правду, то тебя возненавидят люди. Если ты будешь лгать, то тебя возненавидят боги. Но ты должен говорить правду или лгать. Значит, тебя возненавидят люди или возненавидят боги".

Формализуйте также ответ сына: "Если я буду говорить правду, то боги будут любить меня. Если я буду лгать, то люди будут любить меня. Но я должен говорить правду или лгать. Значит, меня будут любить боги или меня будут любить люди".
: Решение. Введем обозначения для логических высказываний: а - "ты будешь говорить правду"; b - "тебя возненавидят люди"; c - "тебя возненавидят боги". Договоримся считать, что некоторое заданное высказывание x истинно, если нет оговорки. Тогда предостережение матери можно записать так:
. А ответ сына - так:
.

Пример 2. Пусть a = "это утро ясное", а b = "это утро теплое". Выразите следующие формулы на обычном языке:

:

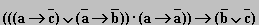
а) "это утро ясное и тёплое"; ж) "это утро не ясное или не тёплое";

б) "это утро ясное и оно не тёплое"; з) "это утро не ясное и не тёплое";

в) "это утро не ясное и оно не тёплое"; и) "это утро ясное или не тёплое";

г) "это утро не ясное или оно тёплое"; к) "если это тро ясное, то оно не тёплое";

д) "это утро ясное или оно не тёплое"; л) "если это утро не ясное, то оно тёплое";

е) "это утро не ясное или оно не тёплое"; м) "это утро ясное и не тёплое".

Пример 3. Из двух данных высказываний a и b постройте составное высказывание, которое было бы:

• а) истинно тогда и только тогда, когда оба данных выказывания ложны;

• б) ложно тогда и только тогда, когда оба данных высказывания истинны.

: а) ; б) .

Пример 4. Из трех данных высказываний a, b, c постройте составное высказывание, которое истинно, когда истинно какое-либо одно из данных высказываний, и только в этом случае.

Ответ: .

4. Логические формулы.

Запишем в форме логического выражения составное высказывание

(2*2=5 или 2*2=4) и (2*2 ≠ 5 или 2*2 ≠ 4)

Проанализируем составное высказывание. Что оно содержит?
Оно содержит два простых высказывания:

А= "2*2=5" - ложно (0)
В= "2*2=4" - истинно (1)

Тогда давайте перепишем составное высказывание. Что получится?

(А или В) и (А или В)

Теперь необходимо записать высказывание в форме логического выражения.
Что нужно сделать для этого?
Нужно подставить знаки логических операций

(AvB)&(AvB)

Теперь выполняем логические операции, причем в строго определенном порядке:

1. отрицание,

2. конъюнкция,

3. дизъюнкция,

4. импликация,

5. эквиваленция

Подставим в логическое выражение значения логических переменных и получим значение логической функции:

F = (AvB)&(AvB) = (0v1) & (1v0) = 1&1 = 1

С помощью логических переменных и символов логических операций любое высказывание можно формализовать, то есть заменить логической формулой.

Определение логической формулы:

Всякая логическая переменная и символы "истина" ("1") и "ложь" ("0") - формулы.

Если А и В - формулы, то ┐А, А . В , А v В , А B , А В - формулы.

Никаких других формул в алгебре логики нет!!!

В качестве примера рассмотрим высказывание "если я куплю яблоки или абрикосы, то приготовлю фруктовый пирог". Это высказывание формализуется в виде (A v B) → C.

Такая же формула соответствует высказыванию "если Игорь знает английский или японский язык, то он получит место переводчика".

Как показывает анализ формулы (A v B) →C, при определённых сочетаниях значений переменных A, B и C она принимает значение "истина", а при некоторых других сочетаниях - значение "ложь". Такие формулы называются выполнимыми.

Некоторые формулы принимают значение "истина" при любых значениях истинности входящих в них переменных. Таковой будет, например, формула А v ┐А , соответствующая высказыванию "Этот треугольник прямоугольный или косоугольный". Эта формула истинна и тогда, когда треугольник прямоугольный, и тогда, когда треугольник не прямоугольный. Такие формулы называются тождественно истинными формулами или тавтологиями.

Высказывания, которые формализуются тавтологиями, называются логически истинными высказываниями.

Если две формулы А и В одновременно принимают одинаковые значения, то они называются равносильными.

Равносильность двух формул алгебры логики обозначается символом "=" или символом "" Замена формулы другой, ей равносильной, называется равносильным преобразованием данной формулы.

5. Связь между алгеброй логикой и двоичной системой счисления.

Математический аппарат алгебры логики очень удобен для описания того, как функционируют аппаратные средства компьютера, поскольку основной системой счисления в компьютере является двоичная, в которой используются цифры 1 и 0, а значений логических переменных тоже два: "1" и "0".

Из этого следует два вывода:

1. одни и те же устройства компьютера могут применяться для обработки и хранения как числовой информации, представленной в двоичной системе счисления, так и логических переменных;

2. на этапе конструирования аппаратных средств алгебра логики позволяет значительно упростить логические функции, описывающие функционирование схем компьютера, и, следовательно, уменьшить число элементарных логических элементов, из десятков тысяч которых состоят основные узлы компьютера.

Данные и команды представляются в виде двоичных последовательностей различной структуры и длины. Существуют различные физические способы кодирования двоичной информации.

В электронных устройствах компьютера двоичные единицы чаще всего кодируются более высоким уровнем напряжения, чем двоичные нули (или наоборот), например:

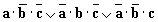
6. Логические элементы компьютера.

Дискретный преобразователь, который после обработки входных двоичных сигналов выдаёт на выходе сигнал, являющийся значением одной из логических операций, называется логическим элементом.

Ниже приведены условные обозначения (схемы) базовых логических элементов, реализующих логическое умножение (конъюнктор), логическое сложение (дизъюнктор) и отрицание (инвертор).

Рис. Конъюнктор, дизъюнктор и инвертор

Устройства компьютера (сумматоры в процессоре, ячейки памяти в оперативной памяти и др.) строятся на основе базовых логических элементов.

Сегодня мы изучим еще один способ представления логических выражений - логические схемы.

Существует три базовых логических элемента, которые реализуют рассмотренные нами три основные логические операции:

• логический элемент «И» - логическое умножение - конъюнктор;

• логический элемент «ИЛИ» - логическое сложение - дизъюнктор;

• логический элемент «НЕ» - инверсию - инвертор.

Поскольку любая логическая операция может быть пред­ставлена в виде комбинации трех основных, любые устройства компьютера, производящие обработку или хранение информации, могут быть собраны из базовых логических элементов, как из "кирпичиков".

Логические элементы компьютера оперируют с сигналами, представляющими собой электрические импульсы. Есть импульс - логический смысл сигнала - 1, нет импульса - 0. На входы логического элемента поступают сигналы-значения аргументов, на выходе появляется сигнал-значение функции.

Преобразование сигнала логическим элементом задается таблицей состояний, которая фактически является таблицей истинности, соответствующей логической функции, только представлена в форме логических схем. В такой форме удобно изображать цепочки логических операций и производить их вычисления.

Пример 1. По заданной логической функции F(A, B) = B& Ú &A построить логическую схему.

Построение необходимо начинать с логической операции, которая должна выполняться последней. В данном случае такой операцией является логическое сложение, следовательно, на выходе логической схемы должен быть дизъюнктор. На него сигналы подаются с двух конъюнкторов, на которые, в свою очередь подаются один входной сигнал нормальный и один инвертированный (с инверторов).

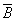
Пример 2. Логическая схема имеет два входа X и Y. Определить логические функции F₁(X,Y) и F₂(X,Y), которые реализуются на ее двух выходах.

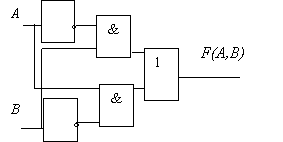
Функция F₁(X,Y) реализуется на выходе первого конъюнктора, т.е. F₁(X,Y) = X&Y.

Одновременно сигнал с конъюнктора подается на вход инвертора, на выходе которого реализуется сигнал , который, в свою очередь, подается на один из входов второго конъюнктора.

На другой вход второго конъюнктора подается сигнал XÚY с дизъюнктора, следовательно, функция F₂(X,Y) = & (XÚY).

Рассмотрим схему сложения двух n-разрядных двоичных чисел. При сложении цифр i-го разряда складываются а_i и b_i, а также p_i-1 - перенос из i-1разряда. Результатом будет s_i - сумма и p_i - перенос в старший разряд. Таким образом, одноразрядный двоичный сумматор - это устройство с тремя входами и двумя выходами.

Пример 3. Построить таблицу истинности одноразрядного двоичного сумматора, воспользовавшись таблицей сложения двоичных чисел.

Входы Выходы

A_i B_i P_i-1 S_i P_i

0 0 0 0 0

0 0 1 1 0

0 1 0 1 0

0 1 1 0 1

1 0 0 1 0

1 0 1 0 1

1 1 0 0 1

1 1 1 1 1

7. Таблицы истинности логических операций.

Таблицу, показывающую, какие значения принимает составное высказывание при всех сочетаниях (наборах) значений входящих в него простых высказываний, называют таблицей истинности составного высказывания.

Составные высказывания в алгебре логики записываются с помощью логических выражений. Для любого логического выражения достаточно просто построить таблицу истинности.

Алгоритм построения таблицы истинности:

1) подсчитать количество переменных n в логическом выражении;

2) определить число строк в таблице, которое равно m = 2ⁿ;

3) подсчитать количество логических операций в логическом выражении и определить количество столбцов в таблице, которое равно количеству переменных плюс количество операций;

4) ввести названия столбцов таблицы в соответствии с последовательностью выполнения логических операций с учетом скобок и приоритетов;

5) заполнить столбцы входных переменных наборами значений;

6) провести заполнение таблицы истинности по столбцам, выполняя логические операции.

Наборы входных переменных, во избежание ошибок, рекомендуют перечислять следующим образом:

а) разделить колонку значений первой переменной пополам и заполнить верхнюю часть колонки нулями, а нижнюю единицами;

б) разделить колонку значений второй переменной на четыре части и заполнить каждую четверть чередующимися группами нулей и единиц , начиная с группы нулей;

в) продолжать деление колонок значений последующих переменных на 8, 16 и т.д. частей и заполнение их группами нулей или единиц до тех пор, пока группы нулей и единиц не будут состоять из одного символа.

8. Основные законы алгебры логики.

Логические выражения называются равносильными, если их истинностные значения совпадают при любых значениях, входящих в них логических переменных.

В алгебре логики имеется ряд законов, позволяющих производить равносильные преобразования логических выражений. Приведем соотношения, отражающие эти законы.

1. Закон двойного отрицания:

А = . Двойное отрицание исключает отрицание.

2. Переместительный (коммутативный) закон:

А v B = B v A; - для логического сложения:

A&B = B&A. - для логического умножения:

Результат операции над высказываниями не зависит от того, в каком порядке берутся эти высказывания.

В обычной алгебре a + b = b + a, a v b = b v a.

3. Сочетательный (ассоциативный) закон:

(A v B) v C = A v (B v C) - для логического сложения:

(A&B)&C = A&(B&C)- для логического умножения:

При одинаковых знаках скобки можно ставить произвольно или вообще опускать.

В обычной алгебре:

(a + b) + c = a + (b + c) = a + b + c,

4. Распределительный (дистрибутивный) закон:

(A v B)&C = (A&C) v (B&C); - для логического сложения

(A&B) v C = (A v C)&(B v C). - для логического умножения:

Определяет правило выноса общего высказывания за скобку.

В обычной алгебре:

(a + b) * c = a * c + b * c.

5. Закон общей инверсии (законы де Моргана):

= &; - для логического сложения

= v - для логического умножения:

6. Закон идемпотентности ( от латинских слов idem - тот же самый и potens -сильный; дословно - равносильный):

A v A = A; - для логического сложения:

A&A = A. - для логического умножения

Закон означает отсутствие показателей степени.

7. Законы исключения констант:

A v 1 = 1, A v 0 = A; - для логического сложения:

A&1 = A, A&0 = 0. - для логического умножения:

8. Закон противоречия:

A&= 0.

Невозможно, чтобы противоречащие высказывания были одновременно истинными.

9. Закон исключения третьего:

A v = 1.

Из двух противоречащих высказываний об одном и том же предмете одно всегда истинно, а второе - ложно, третьего не дано.

10. Закон поглощения:

A v (A&B) = A; - для логического сложения:

A&(A v B) = A. - для логического умножения

11. Закон исключения (склеивания):

(A&B) v (&B) = B; - для логического сложения:

(A v B)&(v B) = B. - для логического умножения:

12. Закон контрапозиции (правило перевертывания):

(A Û B) = (BÛ A).

Справедливость приведенных законов можно доказать табличным способом: выписать все наборы значений А и В, вычислить на них значения левой и правой частей доказываемого выражения и убедиться, что результирующие столбцы совпадут.

В алгебре логики выполняются следующие основные законы, позволяющие производить тождественные преобразования логических выражений:

ОСНОВНЫЕ ЗАКОНЫ АЛГЕБРЫ ЛОГИКИ

Закон Для ИЛИ Для И

Переместительный

Сочетательный

Распределительный

Правила де Моргана

Идемпотенции

Поглощения

Склеивания

Операция переменной с ее инверсией

Операция с константами

Двойного отрицания

9. Составление таблиц истинности.

Согласно определению, таблица истинности логической формулы выражает соответствие между всевозможными наборами значений переменных и значениями формулы.

Для формулы, которая содержит две переменные, таких наборов значений переменных всего четыре:

(0, 0), (0, 1), (1, 0), (1, 1).

Если формула содержит три переменные, то возможных наборов значений переменных восемь:

(0, 0, 0), (0, 0, 1), (0, 1, 0), (0, 1, 1), (1, 0, 0), (1, 0, 1), (1, 1, 0), (1, 1, 1).

Количество наборов для формулы с четырьмя переменными равно шестнадцати и т.д.

Удобной формой записи при нахождении значений формулы является таблица, содержащая кроме значений переменных и значений формулы также и значения промежуточных формул.

1. Составим таблицу истинности для формулы , которая содержит две переменные x и y. В первых двух столбцах таблицы запишем четыре возможных пары значений этих переменных, в последующих столбцах - значения промежуточных формул и в последнем столбце - значение формулы. В результате получим таблицу:

Переменные Промежуточные логические формулы Формула

0 0 1 0 0 1 1 1

0 1 1 1 1 0 1 1

1 0 0 0 1 0 0 1

1 1 0 0 1 0 0 1

Из таблицы видно, что при всех наборах значений переменных x и y формула принимает значение 1, то есть является тождественно истинной.