Урок по химии на тему 'Задачи на сплавы и растворы' (9 класс)

Тема: «Задачи на сплавы и растворы» (интегрированный здоровьесберегающий урок химия-математика)

Цель: показать возможность подготовки обучающихся к ГИА и ЕГЭ на примере решения задач на сплавы и растворы различными способами через интегрированные уроки.

Ход урока:

При решении задач на получение нового раствора из исходных или нового сплава из металлов или сплавов (если дополнительные условия не оговорены в условии задачи) необходимо использовать закон сохранения массы, открытый М.В.Ломоносовым (1748), в общем виде сформулирован А.Лавуазье (1789):

общая масса веществ, вступающих в химическую реакцию, равна общей массе продуктов реакции,

или масса сплава равна сумме масс составляющих его частей и общая масса каждого вещества в сплаве равна сумме масс этого вещества во всех составляющих частях, аналогично и для растворов.

Классификация задач на проценты:

1. Расчеты по уравнению реакций.

2. Задачи на смеси.

3. Задачи на "тип соли" (определение состава продукта реакции).

4. Нахождение массовой доли одного из продуктов реакции в растворе.

5. Нахождение массы одного из исходных веществ по уравнению.

Схема решения задачи по химии

1. Условие задачи

2. Запись уравнения химической реакции

3. Расчеты по химическим уравнениям реакции

4. Запись и интерпретация ответа

Химическая часть задачи:

1. Чтение текста

2. Запись условия задачи

3. Определение типа задачи

4. Анализ задачи - составление плана решения

Математическая часть задачи:

1. Выбор способа решения

2. Решение

3. Запись ответа

4. Анализ решения

Задача (учитель математики)

Первый сплав содержит 5% меди, второй - 13 % меди. Масса второго сплава на 9 кг больше массы первого. Из этих двух сплавов получили третий сплав, содержащий 11% меди. Найдите массу третьего сплава.

1 сплав 5% 2 сплав 13% новый сплав11%

Решение:

Пусть х кг масса 1 сплава.

% меди

Масса сплава

Масса меди

1 сплав

5

х

0,05х

2 сплав

13

х+9

0,13(х+9)

3 сплав

11

х+х+9

0,11(х+х+9)

Составим и решим уравнение.

0,05х+0,13(х+9)= 0,11(х+х+9),

0,18х+1,17=0,22х+0,99,

0,04х=0,18,

х=4,5.

4,5+4,5+9=18(кг)- масса третьего сплава.

Ответ: масса третьего сплава 18 килограмм.

Химический опыт и решение задачи по нему (учитель химии).

Задача

Смешали 300 мл 20%-ного раствора CuCl₂ и 400 мл 30%-ного раствора Na OH. Определите массу полученного раствора.

m _р-ра= 300 г CuCl₂ + 2 NaOH → Cu(OH)₂ ↓ + 2 NaCl

ω(CuCl₂) = 20%= 0,2

m _р-ра= 400 г m _в-ва = ω· m _р-ра

ω(NaOH) = 30%= 0,3 m (CuCl₂) = 300·0,2 = 60 (г)

m (NaOH) = 400·0,3=120 (г)

m(Cu(OH)₂) - ? n (CuCl₂) =

n (CuCl₂) =

n (NaOH)=

Задачу решаем по недостатку CuCl_2.

n (CuCl₂) = n (Cu(OH)₂) = 0,45 моль.

m(Cu(OH)₂) =0,45 моль · 98 г/моль =44,1 (г)

Ответ: m(Cu(OH)₂ ) =44,1 г.

Физкультминутка на движение( можно танцевальную)

Задача

В сосуд, содержащий 10 литров 24%-го водного раствора некоторого вещества, добавили 5 литров воды. Сколько процентов составит концентрация получившегося раствора?

Решение:

Химия

V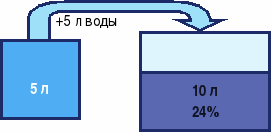_р-ра=10 л V_в-ва= φV_р-ра

φ=24%=0,24 V_в-ва=0,24·10=2,4л

V(H₂O)=5л V_2р-ра=V_1р-ра+V(H₂O)

V_2р-ра=10+5=15л

φ_2в-ва=2,4/15=0,16=16%

Математика

1. 0,24·10=2,4(л)-объём вещества.

2. 10+5=15(л)-объём второго раствора.

3. 2,4:15·100=16%-концентрация нового раствора.

Ответ: 16%.

Задача

Смешали 14 литров 30-процентного водного раствора некоторого вещества с 10 литрами 18-процентного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?

Задача

Смешали 30% и 10% растворы соленой кислоты и получили 600г 15% раствора. Сколько граммов каждого вещества взяли?

Решение:

"Конверт Пирсона":

30%

5%

3 - 450г

600г

15%

5

10%

15%

1 - 150г

600 : (1+3) = 150(г) - 10% раствор.

150·3 = 450(г) - 30% раствор.

Ответ: 150 г и 450 г.

Раствор

масса р-ра

масса к-ты

30%

x

0,3x

10%

y

0,1y

15%

600

0,15·600

I раствор - х г, кислоты - 0,3х г

II раствор - у г, кислоты - 0,1у г

Новый раствор 600 г, кислоты 0,15·600 г

Ответ: 150 г и 450 г.

Аналогичные задачи из ЕГЭ.

Задача В13 (В14)

• В сосуд, содержащий 20 литров 15-процентного водного раствора некоторого вещества, добавили 5 литров воды. Сколько процентов концентрация получившегося раствора?

• В сосуд, содержащий 7 литров 24-процентного водного раствора некоторого вещества, добавили 7 литров воды. Сколько процентов составляет концентрация получившегося раствора?

• Смешали некоторое количество 15-процентного раствора некоторого вещества с таким же количеством 19-процентного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?

• Смешали 4 литра 15-процентного водного раствора некоторого вещества с 6 литрами 25-процентного водного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?

• Первый сплав содержит 10 % меди, второй - 40 % меди. Масса второго сплава больше массы первого на 3 кг. Из этих двух сплавов получили третий сплав, содержащий 30 % меди. Найдите массу третьего сплава. Ответ дайте в килограммах.

• Смешав 30-процентный и 60-процентный растворы кислоты и добавив 10 кг чистой воды, получили 36-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 41-процентный раствор кислоты. Сколько килограммов 30-процентного раствора использовали для получения смеси?

• Имеются два сосуда, содержащие 42 кг и 6 кг раствора кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий 40% кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 50% кислоты. Сколько кг кислоты содержится в первом растворе?

В разработке показано применение «Конверта Пирсона» для решения задач по химии.

Данная тема очень важна в реальной жизни. Ведь часто мы сталкиваемся с необходимостью приготовления раствора нужной концентрации, рассчитать массу вещества в продукте, чистого металла, содержание вредных веществ в воздухе и т.д.

Групповая работа на уроке при закреплении материала. Помимо интегрированного, этот урок и здоровьесберегающий (с физкультминуткой, сменой работы, опытом по химии и т.д.), что так важно в наше время и соответствует требованиям.