1. Элективный курс на тему: изучения основ гидродинамика в 10 классе школьного курса физике [6,5]

Введение

Нам хорошо известны три основных агрегатных состояния вещества (кроме плазмы, являющейся четвертым состоянием вещества): твердое тело, жидкость, газ.

Развитие человеческой цивилизации теснейшим образом связано с использованием водной стихии. Еще в Древней Греции были сделаны первые попытки выяснения механических свойств воды и их использования.

Основным отличием жидкостей от твердых тел, объем и форму которых трудно изменить, даже прилагая значительные усилия, является подвижность (или текучесть) жидкостей, связанная со значительно меньшим, чем в твердых телах сцеплением между молекулами.

Хорошо известно, что жидкость приходит в движение под действием на нее даже очень малых усилий, касательных к ее поверхности. Это - так называемые сдвиговые напряжения, приводящие к нарушению равновесия жидкости, заставляя отдельные ее слои скользить один по другому. При этом сила трения покоя, играющая важную роль при рассмотрении движения твердых тел друг относительно друга, отсутствует, поэтому сила реакции при взаимодействии жидкости с окружающими телами всегда направлена перпендикулярно к поверхности раздела.

Другими словами, жидкость в отличие от твердых тел не обнаруживает никакого сопротивления изменению ее формы. Такая подвижность жидкости объясняет, в частности, то, что свободная поверхность жидкости, находящейся в однородном гравитационном поле, всегда" горизонтальна.

Наука, изучающая механические свойства жидкостей, называется гидромеханикой, ведя свое происхождение от первых опытов изучения движения воды (гидра - по-гречески вода). Частным случаем этой науки является гидростатика - наука о равновесии жидкостей. Именно здесь большую роль играют силы, действующие перпендикулярно к поверхности раздела жидкости, поверхностям стенок сосуда, куда налита жидкость, или поверхности тела при его погружении в жидкость.

Цель элективного курса

1. Изучение основ гидродинамики с помощью демонстраций, визуализирующих течение жидкости.

2. Изучения основ гидродинамика теоретическим методом

3. Изучение свойства песка и жидкости

Задачи элективного курса

1. Углубить знания о понятии давление и законе Паскаля

2. Провести эксперимент по изучению свойств песка и воды

3. Углубить знания о законе Архимеда

4. Провести эксперимент по изучению выталкивающей силы из песка и воды

5. Изучить основы гидродинамики

6. Провести эксперимент по определению формы струи жидкости и песка

7. Теоретическое обоснование форм истечения

8. Обобщение всего курса. Подведение итогов

Содержание

1. Понятие давления в жидкости и газе. Единицы измерения давления. Закон Паскаля. Принцип сообщающихся сосудов. Изменение давления воздуха при подъеме над уровнем моря. (1 ч)

   • Экспериментальное изучение закона Паскаля(1 ч)

   • Обобщение полученных данных по опыту(1 ч)

2. Принцип работы гидравлического пресса и золотое правило механики.(1 ч)

3. Понятие выталкивающей силы (силы Архимеда). Закон Архимеда. Условия справедливости закона Архимеда.(1 ч)

• • • • Опыт на доказательство закона Архимеда с водой и песком(1 ч)

      • Обобщение полученных данных по опыту(1 ч)

4. Основы гидродинамики(2 ч)

5. Эксперимент на Изучение формы струи(1 ч)

6. Обобщение данного опыта(1 ч)

7. Итоговая конференция(1 ч)

Программа элективного курса 10 класс(12 ч)

1. Понятие давления в жидкости и газе. Единицы измерения давления. Закон Паскаля. Принцип сообщающихся сосудов. Изменение давления воздуха при подъеме над уровнем моря. (1 ч)

Если вопрос о том, что такое давление, касается жидкостей или газов, то обычно имеют в виду силу, действующую на единицу площади, а не общую силу. Так, когда хотят узнать достаточно ли воздуха в автомобильной шине, то выясняют это, определяя силу, действующую на 1см², а не общую силу, действующую на всю поверхность шин изнутри.

Давлением в газе (или жидкости) называется величина, равная отношению модуля силы F, действующей по нормали к плоской поверхности, к площади этой поверхности S:

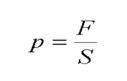(1.1)

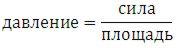
За единицу давления принимается такое давление, которое производит сила в 1 Н, действующая на поверхность площадью 1 перпендикулярно этой поверхности и называется паскалем (обозначается Па).

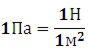
Используются также другие единицы давления: гектопаскаль (гПа) и кило Паскаль (кПа).

1 кПа=1000 Па; 1 гПа = 100 Па ; 1 Па =0,001 кПа; 1 Па 0,01 гПа

Установленный в XVIIIвеке Б. Паскалем (1623-1662) один из основополагающих законов гидростатики, известный как закон Паскаля, утверждает: если на жидкость (или газ), заключенную в замкнутый сосуд производить давление, то это давление передается по всем направлениям во все точки жидкости (газа) и на любую часть внутренней поверхности сосуда без изменения.

Свойство передавать без изменения давление связано с не сжимаемостью жидкости (например, воды) при больших усилиях. Достаточно отметить, что сжатие воды, в частности, под действием атмосферного давления приводит к уменьшению ее объема на

1/20 000 часть исходного объема. В связи с этим в физике вводится представление о "несжимаемости" жидкости, подобно тому, как используется понятие абсолютно твердого тела в механике.

Рассмотрим следующую ситуацию, иллюстрирующую закон Паскаля. Возьмем сосуд, наполненный жидкостью (к примеру, водой), находящейся под неизменным давлением, создаваемым некоторой силой F, приложенной к поршню, основание которого закрывает открытую часть сосуда. Перед тем как закрыть сосуд поршнем поместим в жидкость небольшой полый кубик (например, объемом 1 см³) с тонкими металлическими стенками и площадью грани S_k. На каждую грань этого кубика согласно закону Паскаля будет действовать сила F_k =p · S_k независимо от его ориентации. Если жидкость покоится, то в любой ее малой по размерам части давление будет одинаковым во всех направлениях. Будь это не так, на небольшой кубик в жидкости действовала бы отличная от нуля результирующая сила, и он пришел бы в движение, что противоречит исходному условию равновесия жидкости. Следовательно, 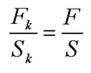или 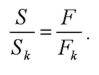Ниже будет показано, что данное соотношение лежит в основе работы гидравлического пресса.

Все эти рассуждения, демонстрирующие закон Паскаля, справедливы в отсутствие силы тяжести, или когда можно ею пренебречь. В этом случае давление во всех точках сосуда будет одинаковым, независимо от формы последнего.

В поле тяжести Земли давление жидкости возрастает с глубиной и численно равно на глубине h весу столба жидкости высотой h и площадью 1 см² .

Давление, которое появляется в жидкости из-за наличия поля тяжести, называется гидростатическим.

Уравнение (1.2) позволяет построить график зависимости давления в жидкости от глубины погружения (рис.1). Так как давление прямо пропорционально глубине h, то его график представляет собой прямую линию (линейную функцию), где 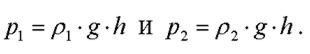Понятно, что наклон прямой давления на графике зависит от плотности жидкости: чем она больше, тем больше давление на одной и той же глубине. На рис. 1 поэтому на глубине h. Если на поверхность жидкости оказывается еще и дополнительное давление , например, земной атмосферы, то полное давление на глубине h будет равно .

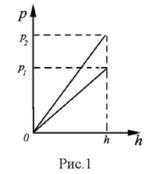
Тогда нетрудно найти разность давлений на двух уровнях жидкости, отстоящих друг от друга по вертикали на расстоянии h₁, что и будет составлять

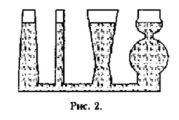
Это, в частности, приводит к тому, что в сообщающихся сосудах, заполненных однородной жидкостью, давление во всех точках жидкости, расположенных на одном уровне, одинаково, независимо от формы сосудов, если наружное давление для всех сосудов одинаково (см. рис.2).

Поэтому в поле тяжести давление в любой точке сосуда не зависит от формы сосуда, а зависит лишь от глубины и плотности жидкости.

Важным следствием предыдущих рассуждений является закон сообщающихся сосудов. Если наливать жидкость в один из сосудов, изображенных на рис.2, то, перетекая через соединения в остальные сосуды, жидкость установится во всех сосудах на одном уровне. Это объясняется тем, что давление на свободных поверхностях жидкости в сосудах одно и то же и равно атмосферному. Вследствие этого все свободные поверхности должны находиться в одной горизонтальной плоскости.

Принцип сообщающихся сосудов используется в устройстве водомерных трубок современных электрочайников и кофеварок. Вода в них устанавливается на том же уровне, что и в объеме чайника. Если на этой трубке нанесены деления, то всегда можно контролировать заливаемый объем воды.

Другая ситуация наблюдается, когда имеются сообщающиеся сосуды с разными жидкостями. Для рассмотрения этого случая возьмем U-образную трубку с открытыми концами и зальем сначала воду с плотностью . Совершенно ясно, что уровень воды в обоих коленах будет одинаков. Доливая теперь в одно из колен другую жидкость, к примеру керосин (с плотностью), который не смешивается с водой, мы заметим, что уровни жидкостей в каждом колене поднимутся, но уже не одинаково (рис.3).

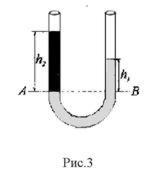
Поверхность раздела между жидкостями (на рис. 3 - уровень АВ) по мере доливания второй жидкости будет опускаться, и вследствие этого возникнет разность уровней h₁ и h₂ жидкостей в коленах U-образной трубки относительно границы раздела АВ.

Определим соотношение между высотами жидкостей в каждом из сосудов над уровнем АВ. Ниже этого уровня в сосудах находится одна и та же жидкость, поэтому давления p_A и p_B в точках А и В, лежащих на одной высоте должны быть одинаковыми. С другой стороны, эти давления равны, исходя из соотношения (1.3)

где p₀ - атмосферное давление. Приравнивая p_A и p_B , получим

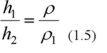
то есть в сообщающихся сосудах высоты столбов жидкостей над уровнем раздела обратно пропорциональны их плотностям. При равенстве давлений высота столба жидкости с большей плотностью будет меньше высоты столба жидкости с меньшей плотностью.

В практике для измерения атмосферного давления используют металлический барометр, называемый анероидом (в переводе с греческого - безжидкостный). Так барометр называют потому, что он не содержит ртути). Для измерения давлений, больших или меньших атмосферного, используют манометры (от греческих слов: м а н о с - редкий, неплотный, м е т р е о - измеряю).

Одним из примеров использования закона сообщающихся сосудов является открытый (жидкостной) манометр, который как раз и состоит из U-образной трубки, заполненной ртутью или другой жидкостью. На одно колено наносится шкала в сантиметрах или миллиметрах, а к другому колену подводится, к примеру, сжатый воздух. Под действием этого воздуха ртуть в одном колене опускается, в другом - поднимается, и возникает разность уровней. Зная разность высот и учитывая удельную плотность ртути, легко найти давление.

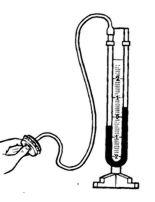
Воздух (как и любой газ) так же, как и жидкость, имеет вес, а значит создает давление, что было впервые открыто Э. Торричелли (1608-1647) в 1643 году. В 1644 году им же был изобретен ртутный барометр, с помощью которого и было впервые измерено атмосферное давление, известное теперь как нормальное.

согласно (1.3) давление у поверхности Земли равно высоте Земной атмосферы, умноженной на ускорение свободного падения и на среднюю по высоте плотность воздуха. Это давление уравновешивается столбиком ртути высотой 760 мм (при нормальных условиях) и называется физической атмосферой, то есть p= 760 мм рт. ст. = 1 физ. атм. В технике до сих пор используется внесистемная единица давления - техническая атмосфера, (технические барометры проградуированы как раз в этих единицах). В частности, давление воздуха на уровне моря близко в среднем к одной физической атмосфере.1 мм рт. ст. = 133,3 Па.

Стеклянная трубка, опущенная вертикально в чашу со ртутью и проградуированная в миллиметрах ртутного столба может служить прибором для измерения атмосферного давления. Этот прибор и был изобретен Торричелли и носит название ртутного барометра. Измерять атмосферное давление можно и столбом воды, только высота соответствующей трубы будет 10.336 м при тех же условиях (водяной барометр).

Атмосферное давление, равное давлению столба ртути высотой 760 мм при температуре 0°С, называется нормальным атмосферным давлением.

Нормальное атмосферное давление равно 101 300 Па = 1013 гПа.

Поднимаясь вверх от уровня моря, мы заметим, что давление воздуха уменьшается. При небольших изменениях высоты, когда плотность воздуха меняется незначительно, атмосферное давление подчиняется линейному закону .

Где p₀ - атмосферное давление на уровне моря, с которого обычно начинается отсчет высоты h (по соглашению). На высоте около 5.5 - 6 км давление и плотность воздуха уменьшаются примерно вдвое.

Примеры решения задач.

№1 Одинаковое ли давление производят на стол кирпичи, расположенные так, как показано на рисунке?

Ответ. Давление, производимое кирпичами, во всех трех случаях одинаковое, так как одинаковы и вес кирпичей и площадь опоры.

№2 Розетки прессуют из специальной массы (карбалитовой), действуя на нее силой 37,5 кН. Площадь розетки 0,0075 м² . Под каким давлением прессуется розетка?

Запись и решение задач в физике производят так:

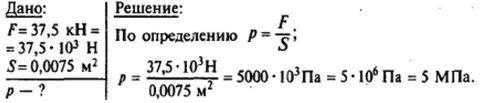
Ответ : p=5МПа.

№3 Токарный станок массой 300 кг опирается на фундамент четырьмя ножками. Определите давление станка на фундамент, если площадь каждой ножки 50 см².

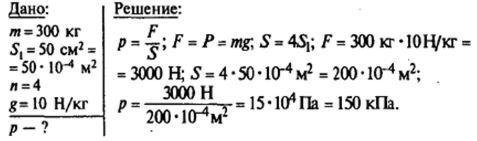
Ответ : p=150кПа.

№4 Высота столба воды в стакане 8 см. Какое давление на дно стакана оказывает вода? Какое давление оказывала бы ртуть, налитая до того же уровня?

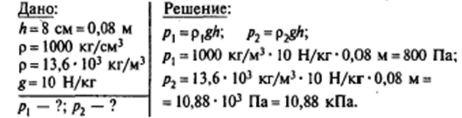
Ответ: p₁=800 Па, p₂=10,88 кПа.

№5 В цилиндрический сосуд налиты ртуть, вода и керосин. Определите общее давление, которое оказывают жидкости на дно сосуда, если объемы всех жидкостей равны, а верхний уровень керосина находится на высоте 12 см от дна сосуда.

Ответ : p=6,16кПа.

• Экспериментальное изучение закона Паскаля(1 ч)

Проведем следующий опыт для изучения давления на разные виды жидкости(песок, вода).

Если заполнить одинаковые по размерам сосуды: один - жидкостью, другой - сыпучим материалом (например горохом), в третий поставить вплотную к стенкам твердое тело, на поверхность вещества в каждом сосуде положить одинаковые кружочки, например, из дерева /они должны прилегать к стенкам /, а сверху установить одинаковые по массе грузы,

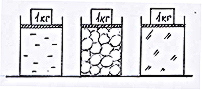
то как изменится давление вещества на дно и стенки в каждом сосуде.

2. Принцип работы гидравлического пресса и золотое правило механики.(1 ч)

Закон Паскаля позволяет объяснить принцип действия гидравлического пресса, который состоит из двух сообщающихся между собой цилиндрических сосудов разного диаметра, снабженных поршнями (рис.4).

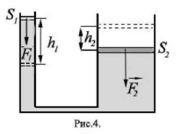
Пространство под поршнями заполнено жидкостью (обычно маслом). Обозначим площадь малого поршня через S₁, а большого как S₂. Пусть к малому поршню приложена сила. Найдем какую силу F₂ необходимо приложить ко второму поршню, чтобы сохранить равновесие, то есть скомпенсировать усилие, приложенное к первому поршню. Другими словами, жидкость не должна быть вытеснена из первого цилиндра во второй и обратно.

Давление под первым поршнем будет равно ,

а под вторым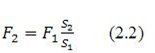

то есть сила F₂ во столько раз больше силы F₁ ,во сколько площадь второго поршня больше площади первого. Таким образом, с помощью гидравлического пресса можно малым усилием уравновесить большую силу. Предположим, теперь что первый поршень переместился (например, опустился) на расстояние h₁ (рис.4). Тогда часть жидкости будет вытеснена из первого цилиндра во второй, приподнимая второй поршень на высоту h₂ . Если считать жидкость несжимаемой, то на основе равенства объемов вытесненной из первого цилиндра жидкости и поступившей во второй можно записать , то есть h₁ · S₁ = h₂ · S₂ , то есть

Сравнивая это соотношение с формулой (2.2), видим, что путь, проходимый поршнем с большей площадью, во столько раз меньше пути, проходимого поршнем с меньшей площадью, во сколько раз сила, действующая на больший поршень больше силы, действующей на меньший поршень. Подставляя (2.3) в (2.2), получим, что работа, совершаемая силой F₂ пути h₂ равна работе, совершаемой силой F₁ на пути h₁

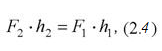
то есть выполняется закон сохранения энергии. Кроме того, в рассматриваемом случае имеет место полная аналогия с соотношением между путями, проходимыми концами рычага, и силами, к ним приложенными. Другими словами, здесь выполняется золотое правило механики, гласящее, что во сколько раз выигрываем в силе, во столько раз проигрываем в расстоянии.

Примеры решения задач.

№1 Площадь меньшего поршня гидравлического пресса 10 см² . На него действует сила 200 Н. Площадь большего поршня 200 см². Какая сила действует на больший поршень?

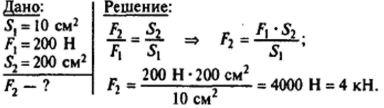
Ответ: F₂=4 кН.

№2 Малый поршень гидравлического пресса под действием силы 500 Н опустился на 15 см. При этом большой поршень поднялся на 5 см. Какая сила действует на большой поршень?

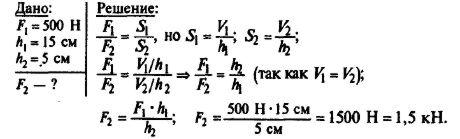
Ответ: F₂=1,5 кН.

№3 Какой выигрыш в силе можно получить на гидравлических машинах, у которых площади поперечных сечений поршней относятся как: а) 1:10; б) 2:50; в) 1:100; г) 5:60; д) 10:100?

Ответ: а) Выигрыш в 10:1=10 раз; б) выигрыш в 50:2=25 раз; в) выигрыш в 100:1=100 раз; г) выигрыш в 60:5=12 раз; д) выигрыш в 100:10=10 раз.

№4 Выполняется ли закон сообщающихся сосудов на искусственном спутнике Земли?

Ответ. Нет. В условиях невесомости столб жидкости не оказывает давления на дно и стенки сосуда, жидкость находится в состоянии невесомости и может располагаться в сообщающихся сосудах как угодно, занимая такой объем, чтобы площадь свободной поверхности жидкости была минимальной.

3. Понятие выталкивающей силы (силы Архимеда). Закон Архимеда. Условия справедливости закона Архимеда.(1 ч)

Другим основополагающим законом гидростатики является закон Архимеда, открытый по преданиям греческим ученым и мыслителем Архимедом (ок. 287 - 212 до н. э.). Этот закон гласит: "На тело, погруженное в жидкость или газ, действует выталкивающая сила, равная весу жидкости (или газа) в объеме погруженной части тела". Возникновение этой силы легко понять на таком простом примере. Погрузим брусок высотой Lи площадью основания Sв жидкость с плотностью, не равной плотности погружаемого тела

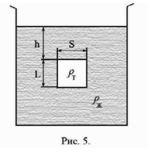
На поверхность тела, опущенного жидкость, действуют силы давления, которые увеличиваются с глубиной погружения. Силы, с которыми жидкость действует на боковые грани бруска, попарно равны и уравновешивают друг друга. Сила, действующая со стороны жидкости на нижнюю поверхность бруска, направлена вертикально вверх и равна по величине (как это следует из соотношений (1.1) и (1.2)):

Выталкивающая сила, называемая еще силой Архимеда, - это алгебраическая сумма всех сил, действующих на поверхность погруженного в жидкость тела, со стороны жидкости (рис.6).

В нашем случае результирующая сила равна

где

- масса жидкости, вытесненная бруском. Итак, на тело действует сила, направленная вертикально вверх и равная весу вытесненной жидкости. В поле земного тяготения эта сила направлена против силы тяжести самого тела и приложена в центре тяжести вытесненного объема жидкости. Эту точку называют центром давлений, потому что выталкивающая сила есть результирующая всех сил давлений со стороны жидкости на поверхность погруженного в нее тела.

Закон Архимеда справедлив и в случае, когда тело плавает в жидкости или частично опущено в нее через свободную, то есть не соприкасающуюся со стенками сосуда, поверхность жидкости. Закон Архимеда позволяет объяснить, почему одни тела плавают, а другие тонут; почему стальная пластина тонет, а огромные стальные корабли плавают; почему тяжелое тело становится гораздо легче в воде. Во всех этих случаях для объяснения явления достаточно сравнить величины выталкивающей силы и силы тяжести, которые направлены противоположно друг другу.

1) если сила тяжести больше архимедовой силы, то тело будет опускаться на дно, тонуть, т. е. если F > F_A ,то тело тонет;

2) если сила тяжести равна архимедовой силе, то тело может находиться в равновесии в любом месте жидкости, т. е. если F = F_A, то тело плавает внутри жидкости;

3) если сила тяжести меньше архимедовой с

Если тело плавает в жидкости, то вес вытесненной им жидкости равен весу этого тела в воздухе. Легко доказать, что если плотность сплошного твердого тела больше плотности жидкости, то тело в такой жидкости тонет. Тело с меньшей плотностью всплывает в этой жидкости. Тело же, плотность которого равна плотности жидкости, остается в равновесии внутри жидкости. Кусок железа, например, тонет в воде, но всплывает в ртути. Закон Архимеда применим и к телам, находящимся в воздухе. В этом случае на тело действует выталкивающая сила, равная весу воздуха в объеме тела, что необходимо учитывать при точном взвешивании тел.

Закон Архимеда иногда формулируют и так: тело, погруженное в жидкость или газ, теряет в своем весе столько, сколько весит вытесненная им жидкость или газ.

Примеры решения задач.

№1Стальной брусок, вес которого 15,6 Н, погрузили в воду. Определите значение и направление силы натяжения пружины.

Ответ: F_H = 13,6 H.

№2 Плот состоит из 12 сухих еловых брусьев. Длина каждого бруса 4 м, ширина 30 см и толщина 25 см. Можно ли на этом плоту переправить через реку автомашину весом 10 кН?

Ответ: F_под = 14,4 кH.

№3 Судно, погруженное в пресную воду до ватерлинии, вытесняет воду объемом 15 000 м³. Вес судна без груза равен 5 • 10⁶ Н. Чему равен вес груза?

• Опыт на доказательство закона Архимеда с водой и песком

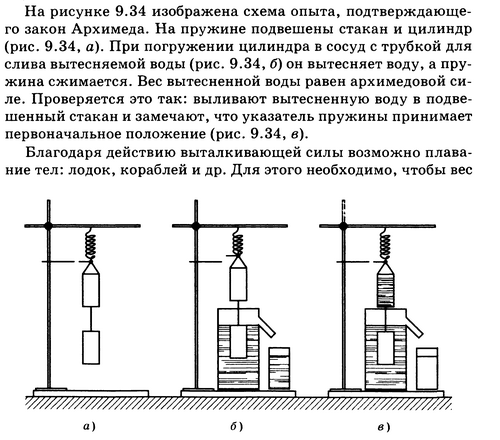
Рис.9.34

4. Основы гидродинамики(3 ч)

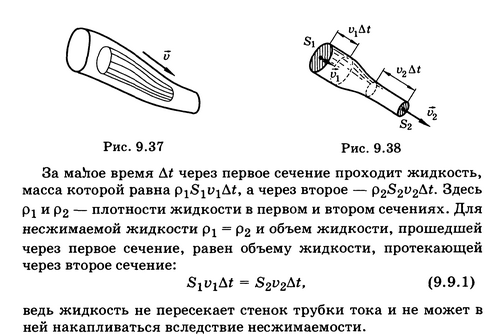
Уравнение Бернулли

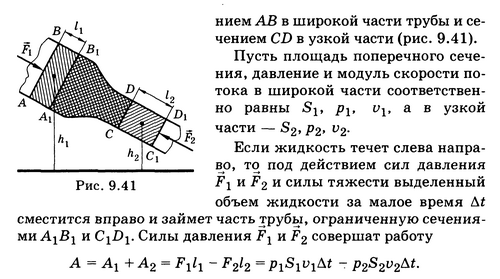
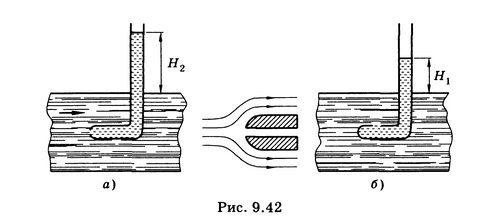
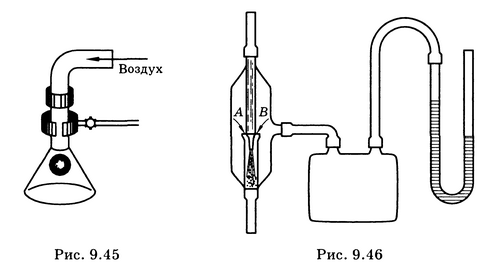
Изучение формы струи

В данной работе исследуется истечение ньютоновской жидкости (воды), струйное течение сыпучих материалов (песок), а так же течение нанопорошка. Для экспериментальной работы используются следующая установка (Рис. №3):

Рис. №3 Лабораторная установка

• лабораторный штатив

• 3 муфт

• 3 лапки

• стеклянная прозрачная трубка длинною 1 метр и диаметром 4 сантиметра;

• сосуд для исследуемых веществ с регулятором потока, высотой порядка 18 сантиметров и диаметром отверстия для истечения 1,5 сантиметра;

• колба, объёмом 250 миллилитров.

• стеклянная воронка

Лабораторный штатив ставился на стол, и на него закреплялась стеклянная трубка, так что бы ее нижняя часть могла быть опущена в колбу, стоящую на полу. Диаметр колбы 6 см. Чтобы исследуемое вещество полностью оставалось в колбе разность между диаметрами закрывалось скрученным листом бумаги и закреплялось на трубке 2 скрепками.

Трубка выравнивалась по уровню, для идеального течения жидкости по ней. Сверху трубы закреплялся резервуар и выравнивался с помощью уровня так, что бы исследуемое вещество истекало строго по центру трубы.

Для фиксирования течения воды, песка и нанопорошка использовалась

фотокамера olympus с 5 кратным увеличением и камерой 14 мегапикселей. Выдержка данного фотоаппарата составляет 0,0005 с

Цель работы:

Исследования течения песка, воды и нанопорошка.

Задачи работы:

• Провести эксперимент с ньютоновской жидкостью (водой) и сыпучими веществами (песок и нанопорошок).

• Зафиксировать данные по полученным результатам фотокамерой и обработать фотографии на компьютере

• сделать вывод из полученных данных путём анализа фотографий и делать соответствующие предположения по данной тематике.

2. Струйное течение ньютоновской жидкости.

Анализ экспериментальных данных

Проведен эксперимент по изучению истечения ньютоновской жидкости (воды) и в ходе данного эксперимента получены следующие данные:

Рис. №4 Область ламинарного течения

Рис. № 5 Переходный слой

Рис. № 6 Область турбулентного течения

Были выявлены 3 области течения струи воды:

• Ламинарное течение Рис.№4

• Переходный слой Рис. №5

• Область турбулентного течения Рис. № 6

Как видно на Рис. № 4 при удалении от отверстия истечения диаметр струи начинает уменьшаться.

На Рис. №5 изображен переходный слой, когда диаметр струи до некоторой точке сужается, но после нее начинает увеличиваться пограничный слой и в нем возникает турбулентность.

На Рис. № 7 видна отчетливо турбулентность жидкости.

Для обоснования полученных результатов, найдем теоретическим путем уравнения, описывающее форму и поведения ламинарного течения. Описание теории турбулентности струи очень сложна и до конца не изучена и поэтому данную теорию мы рассматривать не будем.

Поиск формы струи и распределение скоростей в ней.

В работе [7] указано, что имеется отверстие радиуса а (рис. №7) , из которой вытекает струя идеальной жидкости (υ=0), не подверженная возмущениям. Течение под влиянием сил тяжести ускоряется, скорость увеличивается и поэтому сечение сужается.

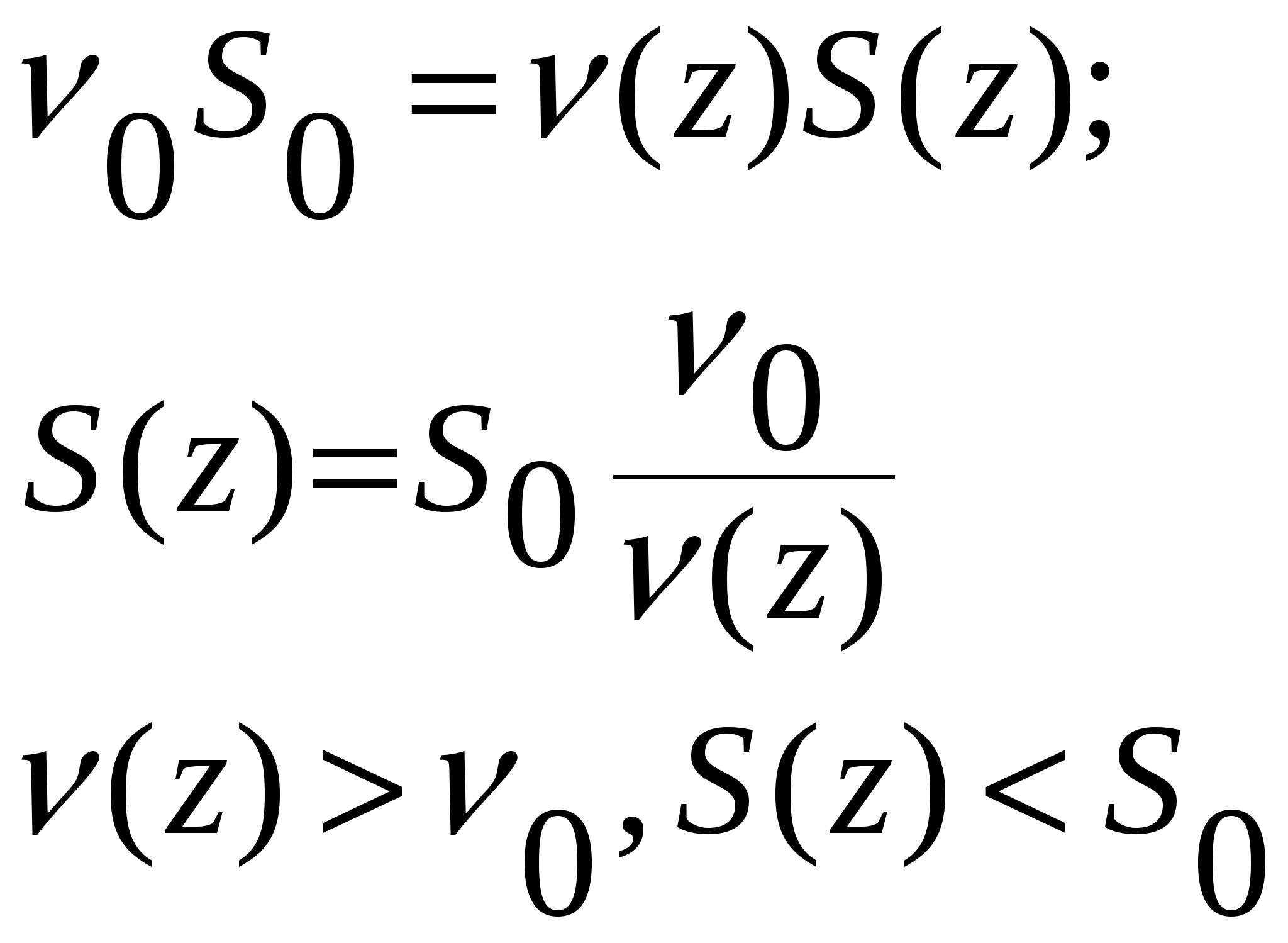
Рис. №7 Область ламинарного течения

Требуется найти форму струи и распределение скоростей в ней.