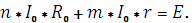
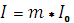
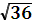
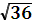
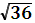
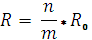
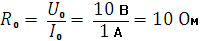
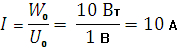
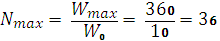
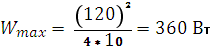
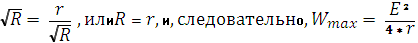
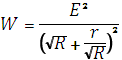
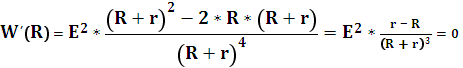
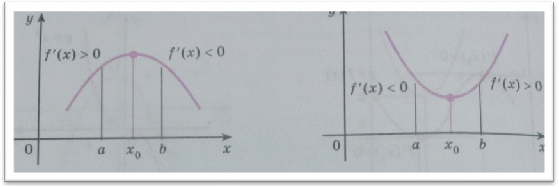
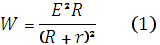
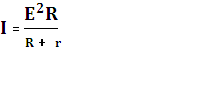
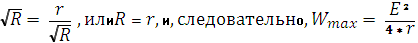
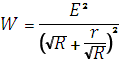
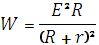Муниципальное бюджетное учреждение дополнительного образования

«Центр детского технического творчества»

Тема исследования: «СОСТАВЛЕНИЕ ЕЛОЧНОЙ ГИРЛЯНДЫ»

Выполнил: Е.В.Малков

Научный руководитель: Е.В. Асмолова,

2015

СОДЕРЖАНИЕ

ВВЕДЕНИЕ..............................................................................................3

Раздел I Составление елочной гирлянды…...…………………………….4-9

1.1. История появления елочной гирлянды….............................................4-7

1.2. Способы составления самодельных гирлянд.......................................7-9

РазделIIМатематические аспекты темы………......................................9-12

2.1.Функции и графики……………………...........................................9-10

2.2. Начала математического анализа…………………………………..10-11

2.3. Развитие понятия о числе…..........................................................11-12

Раздел III Практическая реализация темы……………………………12-20

ЗАКЛЮЧЕНИЕ.........................................................................................21

БИБЛИОГРАФИЧЕСКИЙ СПИСОК ........................................................22

ПРИЛОЖЕНИЕ……………………………………………....………….23-25

ВВЕДЕНИЕ

Актуальность темы.

Гирлянды - обязательная составляющая украшения новогодней елки. Этот декор для ели можно увидеть в каждом доме, потому что именно она придает волшебный блеск и красоту елке. Именно она привносит праздник и сказку в Новый год. Конечно, елочную гирлянду можно купить в любом магазине, но можно и сделать своими руками. Проведя социологический опрос, мы убедились в необходимости разработки темы данной научно - исследовательской работы.

Текущий интерес к теме составления елочной гирлянды объясняется широким применением елочным гирлянд для украшения всего дома и создания праздничного настроения.

Целью данной работы является теоретическое и практическое обоснование принципа составления елочной гирлянды.

В связи с актуальностью нами сформулирована тема исследования: «Составление елочной гирлянды».

Проблема исследования: изложить основные идеи по составлению елочных гирлянд.

Гипотеза: составление елочной гирлянды будет обеспечено, если будут выполнены все условия для грамотного применения законов физики, математической теории.

Предмет исследования: процесс составления елочной гирлянды.

Задачи:

- определить способы изготовления елочной гирлянды;

- выявить математический аспект темы;

- решить задачу по составлению елочной гирлянды

Раздел I Составление елочной гирлянды

1. История появления елочной гирлянды

Наряду с елочными игрушками, переливающиеся всеми цветами и радостно мигающие огоньки - гирлянды - являются неотъемлемым элементом новогоднего украшения. Но в отличие от игрушек, история современной электрической гирлянды началась относительно недавно.

Существует библейское предание о том, как появившегося на свет Христа хотели поздравить с рождением деревья - пальма, маслина и ель. Но Ели нечего было преподнести младенцу, кроме своей колючей хвои и липкой смолы - и подруги-деревья осмеяли её. Ангел наблюдал за происходящим и пожалел скромное дерево, по мановению его руки звезды с неба украсили колючие ветви множеством ярких огоньков, и именно к ним, веселым огонькам, потянулся проснувшийся божественный младенец.

До изобретения электрической гирлянды елки украшались бумажной мишурой и свечами. Эта традиция уходит корнями в далекое прошлое - еще у римлян привязанные к дереву ленточки считались символом плодородия и возрождения жизни. Уже позже, в XV-XVI веках, в Европе стали использовать для украшения горящие свечи, которые были призваны отпугивать злых духов от дома. В России, традиция, связанная с обязательным украшением ёлки новогодними огнями, берёт свое начало с далекого 1700 года. Именно тогда любителем реформ Петром I был издан приказ, связанный с использованием обычных свечей в качестве незаменимого елочного украшения. Петр I принес эту традицию и в Россию. Однако при кажущейся безобидности эти украшения таили в себе немалую опасность: открытый огонь, еще и в сочетании с мишурой, создавал опасность возникновения пожара. Поэтому для украшения елки требовалось что-то столь же яркое и веселое, но менее опасное, что позволяло бы не следить за безопасностью помещения постоянно.

Настоящей находкой стали электрические лампы. После изобретения Эдисоном лампы накаливания они стали проникать во все сферы жизни, в том числе и в украшение дома к Новому году. Существует несколько версий возникновения электрической гирлянды. По одной из них, первую гирлянду придумал и воплотил в жизнь помощник самого Эдисона - инженер Эдвард Джонсон. В 1882 году он соединил проводом окрашенные в разные цвета лампочки. Однако его изобретение не обрело серьезного успеха. Это было связано с технологической трудностью подключения гирлянды - ее владельцу нужно было самомуприсоединить концы провода к электродам каждой из лампочек, а затем подвести основной провод к источнику питания; в то время немногие способны были это сделать самостоятельно.

Другие источники утверждают, что электрическую гирлянду изобрел американец Ральф Моррис, сотрудник телефонной компании, который постоянно работал с электролампами в распределительных щитах. В канун 1895 года он предложил использовать их и для украшения елки. Задумка была реализована довольно успешно: к тому времени значительное число людей уже было тесно знакомо с электрическими приборами, поэтому для них не составляло сложности самостоятельно подключать гирлянду. Первая электрическая гирлянда была использована для украшения елки перед Белым Домом в 1895 году.

Так или иначе, постепенно новое изобретение добралось до Европы. Впервые в 1906 году электрическими гирляндами было украшено несколько елок в столице Финляндии.

В дореволюционное время ее использование осуждалось Священным синодом как «германское изобретение», а позже сказались сложное экономическое положение государства и гражданская война. Лишь в 1938 году в России наконец начался выпуск электрогирлянд.

Конечно, образцы 30-х годов прошлого столетия кардинально отличались от современных. Это были обычные автомобильные лампочки, покрашенные лаками и красками и припаянные к одному проводу. Несмотря на крайнюю простоту, гирлянды «Московского электролампового завода» были крайне популярны. Это вполне объяснимо, ведь в военные годы было не до излишеств. Изначально, электрические гирлянды стоили так дорого, что их чаще брали напрокат, чем покупали. В начале XX века елка, украшенная электрическими гирляндами, свидетельствовала о состоятельности владельцев. Эти гирлянды были почти также опасны, как и свечи, так как они часто становились причиной пожара - ламповое стекло накалялось настолько, что хвоя вспыхивала. Тогда бытовало убеждение, что электрические лампочки будут гореть дольше, если их установить строго вертикально. Производителям гирлянд потребовались годы, чтобы изготовить цепи с вертикально торчащими лампочками. Однако вскоре выяснилось, что это убеждение было ошибочным.
В Советской России первые гирлянды начали производить только в 1938 году, потому что во время Первой мировой войны, в 1916 году, Священный Синод посчитал ёлку «немецким обычаем» и осудил её использование. Через несколько лет после Октябрьской революции, в 1924 году, власти запретили Рождество, считая его «поповским праздником».
И только в конце 1935 года людям было разрешено официально праздновать Новый год, с наряженными ёлками.

В конце 50-х появляются гирлянды из лампочек-фигурок: медвежонка, поросенка, дирижабля, автомобиля и т. д. Внутри фигурки из толстого стекла закреплялась нить накаливания, а сама фигурка вставлялась в цоколь, который был закреплен на проводе.

С течением времени гирлянда прошла ряд изменений в ее форме и принципе работы. Изначально это были просто соединенные проводом лампочки. В дальнейшем использовались плафоны в форме звездочек или цветочков. С развитием электроники возникли блоки управления, позволяющие задавать различные режимы работы отдельных элементов.

В наше время существует несколько видов электрических гирлянд. Кроме привычной линейной конструкции, когда лампочки расположены на проводе одна за другой, есть и более сложные образцы, например, так называемый «световой занавес» или «световая сеть». Или «дюралайт» и «гибкий неон», в которых лампочки спрятаны внутри гибкого шнура, способного защитить их от внешних погодных воздействий и соприкосновения поверхности с нагретыми элементами.

Но самым значимым изменением в устройстве электрогирлянды стал переход к светодиодам в качестве светящих элементов. Они более безопасные и экономичные, меньше греются и светят ярче, к тому же служат куда дольше.

1.2. Способы составления самодельных гирлянд.

1. Новогодние гирлянды своими руками с применением понижающего трансформатора.

Лампочки нужно подобрать невысокого напряжения: 1,5; 2,5; 6 Вольт. Можно применить лампочки для карманного фонарика. Соединим их параллельно с трансформатором, как изображено на рис.1 и гирлянда электрическая готова. Естественно, напряжение вторичной обмотки понижающего трансформатора должно полностью соответствовать напряжению, на которое рассчитаны лампочки. Но чаще, в современных гирляндах не применяют трансформаторы. Можно ли изготовить электрическую гирлянду самостоятельно без понижающего трансформатора. Конечно, можно!

Рис.1

2. Новогодние гирлянды своими руками без применения понижающего трансформатора.

В этом случае лампочки нужно соединить последовательно, как это сделать смотри рис.2

Рис. 2

Но точное соединение- это еще не все, нужно правильно рассчитать количество ламп в елочной гирлянде. Для этого напряжение в розетке разделим на напряжение лампочки. Напряжение в розетке известное - 220 Вольт. Теперь рассчитаем сколько лампочек можно включить в состав гирлянды. К примеру, выберем лампочки на напряжение 2,5 вольта, то тогда общее число лампочек будет 220 разделить на 2,5 равно 88 лампочек. Соединяем лампочки как показано на рисунке и елочная гирлянда готова. ВНИМАНИЕ! Нужно помнить, с электричеством нужно обращаться очень осторожно. Перед включением все части гирлянды должны быть надежно соединены, оголенные части изолированы.

3. Искусственный снегопад.

Приобретите некоторое количество автомобильных лампочек на 6 или 12 Вольт. Можно брать лампочки от обыкновенных фонарей. Соедините эти лампочки между собой гибкими изолированными проводами, используя параллельное соединение. Приготовьте 5-6 таких же гирлянд и раскрасьте лампочки разноцветными красками. Придумайте контактор, соедините его редуктором и с вентилятором электродвигателя и подключите к контактору гирлянды, расположенные на новогодней елке по спирали. Включите электродвигатель, и ваши гирлянды будут постепенно включаться в цепь, создавая яркий свет, бегущий снизу вокруг новогодней елки. Схема соединения елочных гирлянд к цепи контактора имеет последовательную структуру.

А далее прибор для автоматического включения елочных гирлянд

Для автоматического включения и выключения елочных гирлянд, цепей электрифицированных макетов можно изготовить простейшее биметаллическое реле, состоящее из биметаллической пластинки и неподвижного контакта.

Наиболее приспособленными для изготовления пластинки являются вещества цинк и железо, обладающие различными моментами коэффициента расширения. Из этих металлов создайте две полоски, соедините их вместе, Сделайте несколько дырок по всей длине и соедините их заклепками.

На деревянной заготовке укрепите стенной патрон, стойку с клеммами и укрепленной биметаллической пластинкой, которая согревается лампочкой. Когда пластинка достаточно нагреется, то задвинется в сторону, размыкая цепь, например елочной новогодней гирлянды. В это время не работает и лампочка, нагревающее пластинку. Остыв, пластинка снова двигается в первоначальное положение и снова соединяет электрическую цепь, и т. д.

Раздел II Математические аспекты темы.

Для грамотного составления гирлянд необходимо иметь знания по математике, электротехнике и физике.

2.1. Функции и графики

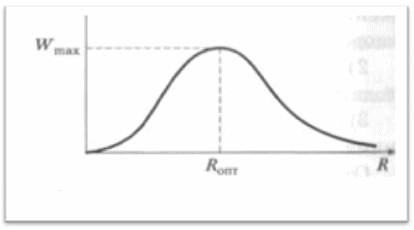
Нарисуйте примерный график функции W(R)и определите характер такой зависимости, ответив на следующие вопросы:

1. каков знак функции W(R)при R> 0;

2. к какому пределу стремится W(R) при R→ 0;

3. к какому пределу стремится W(R) при R → ∞;

4. является ли функция W(R)непрерывной;

5. имеются ли у функции W(R)экстремумы при Rе (0; ∞)?

После ответов на приведенные вопросы очевидно, что при R>0

W> 0, а при R→ 0 W→ 0 и при R→ ∞ W→ 0, т. е. функция имеет максимум при некотором R_опт (рис. 3).

Для нахождения точки максимума можно продифференцировать функцию W(R).

Ответы:

1) знак функции при R> 0, W > 0;

2) при R → 0 стремиться к пределу W → 0;

3) при R → ∞ стремиться к пределу W → 0;

4) Да, функция W(R) является непрерывной;

5) Да, у функции W(R) экстремумы имеются.

2.2. Начала математического анализа

Начала математического анализа.

Вычислите производную функции W(R) и ответьте на следующие вопросы:

1. как связана монотонность функции со знаком производной;

2. как меняется знак W'(R);

3. что является необходимым условием экстремума функции;

4. что является достаточным условием экстремума функции?

Ответы:

1)Если f'(x)>0 на промежутке, то функция возрастает на этом промежутке, но если f'(x)<0, то функция убывает на этом промежутке ;

2) Если W'(R) от 0 до R_опт, то W'(R)>0, но если W'(R)<0, то от R_опт до ∞

3) Необходимо чтобы точки, в которых функция имеет производную, равную нулю, или не дифференцируема была критической точкой этой функции;

4) Приведём достаточные условия. Пусть функция f (х) дифференцируема на интервале (а;b), х₀ є (а; b), и f' (х₀) = 0. Тогда: а) если при переходе через стационарную точку х₀функции f (х) ее производная меняет знак с «плюса» на «минус», т. е. f^' (x) > 0 слева от точки х₀и f' (х) < 0 справа от точки х₀, то х₀ - точка максимума функции f (х);

б) если при переходе через стационарную точку х₀функции f (х) ее производная меняет знак с «минуса» на «плюс», то х₀ - точка минимума функции f (х).

Из ответов на приведенные вопросы ясно, что в точке максимума W'(R) = 0. Тогда получаем

Т.е.

Но кто еще не изучал производную, тем нужно преобразовать функцию. Функция W(R) зависит сложно от R, причем зависимость от R присутствует как в числителе, так и в знаменателе дроби. Можно упростить выражение
, поделив числитель и знаменатель на R:

Ясно, что мощность W будет максимальной при минимальном знаменателе. Нужно применить неравенство о среднем арифметическом и среднем геометрическом.

2.3. Развитие понятия о числе

Напишите неравенство о среднем арифметическом и среднем геометрическом и ответьте на следующие вопросы:

1. для каких чисел справедливо неравенство о среднем арифметическом и среднем геометрическом;

2. при каком условии неравенство о среднем арифметическом и среднем геометрическом переходит в точное равенство;

3. если сумма нескольких чисел равна постоянному числу, то в каком случае их произведение максимально;

4. если произведение нескольких чисел равно постоянному числу, то в каком случае их сумма минимальна?

Ответы:

1)Среднем арифметическим любых n чисел а1, а2,… , аn называется число

Среднем геометрическим n положительных чисел

а1, а2,… , аn называется число

2) Для описания точности вычислений применяется

термин погрешность. Если точное значение величины равно x,

а вычисленное приближенное значение равно a, то

погрешностью вычисления называется модуль разности

точного и приближенного значений, т. е. число |x - a|

3) а1 * а2 * а3 = R

4) а1 * а2 * а3 = n, но если одно из чисел отрицательно

Раздел III Практическая реализация темы

Задача.

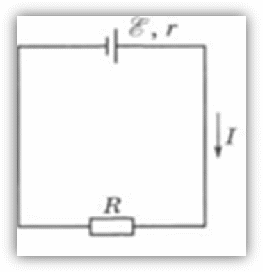
Семья Малковых решила встречать Новый год на даче. На участке росла прекрасная елка, и папа решил украсить ее электрической гирляндой. В сарае оказались аккумуляторная батарея с ЭДС = 120 В и внутренним сопротивлением r = 10 Ом и большое количество электрических лампочек, рассчитанных на напряжение U₀ = 10 В и мощность W₀ = 10 Вт. Движимый желанием сделать украшение наиболее эффектным, папа обратился к старшему сыну Евгению, обучающемуся в индустриальном колледже, с просьбой рассчитать максимальное количество лампочек, которые при соединении в гирлянду будут гореть полным накалом?

Решение.Евгений сначала решил задачу, как можно наиболее эффективно использовать батарею, т. е. какую максимальную полезную мощность можно получить от нее (на сопротивлении Rв цепи, рис. 3).

Рис.3

При этом ему пришлось вспомнить некоторые сведения, полученные на занятиях по физике и электротехнике. Мощность, выделяемая на сопротивлении R,определяется законом Джоуля - Ленца:

W =I²*R,

где I - ток в цепи, который можно найти из закона Ома для полной цепи:

Таким образом, выделяемая во внешней цепи мощность зависит от сопротивления R:

Нарисуем график функции W(R)и определим характер такой зависимости, ответив на следующие вопросы:

1. каков знак функции W(R)при R> 0;

2. к какому пределу стремится W(R) при R→ 0;

3. к какому пределу стремится W(R) при R → ∞;

4. является ли функция W(R)непрерывной;

5. имеются ли у функции W(R)экстремумы при Rе (0; ∞)?

Рис.4

После ответов на приведенные вопросы очевидно, что при R>0

W> 0, а при R→ 0 W→ 0 и при R→ ∞ W→ 0, т. е. функция имеет максимум при некотором R_опт (рис. 4).

Для нахождения точки максимума можно продифференцировать функцию W(R).

Ответы:

1) знак функции при R> 0, W > 0;

2) при R → 0 стремиться к пределу W → 0;

3) при R → ∞ стремиться к пределу W → 0;

4) Да, функция W(R) является непрерывной;

5) Да, у функции W(R) экстремумы имеются.

Вычислим производную функции W(R) и ответим на следующие вопросы:

1. как связана монотонность функции со знаком производной;

2. как меняется знак W'(R);

3. что является необходимым условием экстремума функции;

4. что является достаточным условием экстремума функции?

Ответы:

1)Если f'(x)>0 на промежутке, то функция возрастает на этом промежутке, но если f'(x)<0, то функция убывает на этом промежутке ;

2) Если W'(R) от 0 до Rопт, то W'(R)>0, но если W'(R)<0, то от Rопт до ∞

3) Необходимо чтобы точки, в которых функция имеет производную, равную нулю, или не дифференцируема была критической точкой этой функции;

4) Приведём достаточные условия. Пусть функция f (х) дифференцируема на интервале (а;b), х₀ є (а; b), и f' (х₀) = 0. Тогда:

а) если при переходе через стационарную точку х₀функции f (х) ее производная меняет знак с «плюса» на «минус», т. е. f^' (x) > 0 слева от точки х₀и f' (х) < 0 справа от точки х₀, то х₀ - точка максимума функции f (х) (рис. 5);

б) если при переходе через стационарную точку х₀функции f (х) ее производная меняет знак с «минуса» на «плюс», то х₀ - точка минимума функции f (х) (рис. 6).

Рис.5рис.6

Из ответов на приведенные вопросы ясно, что в точке максимума W'(R) = 0. Тогда получаем

Т.е.

Но Александр еще не изучал производную и попробовал преобразовать функцию. Функция W(R) зависит сложно от R, причем зависимость от R присутствует как в числителе, так и в знаменателе дроби. Можно упростить выражение (1), поделив числитель и знаменатель на R:

Ясно, что мощность W будет максимальной при минимальном знаменателе. Александр вспомнил, что есть неравенство о среднем арифметическом и среднем геометрическом.

Напишем неравенство о среднем арифметическом и среднем геометрическом и ответим на следующие вопросы:

1. для каких чисел справедливо неравенство о среднем арифметическом и среднем геометрическом;

2. при каком условии неравенство о среднем арифметическом и среднем геометрическом переходит в точное равенство;

3. если сумма нескольких чисел равна постоянному числу, то в каком случае их произведение максимально;

4. если произведение нескольких чисел равно постоянному числу, то в каком случае их сумма минимальна?

Ответы:

1)Среднем арифметическим любых n чисел а1, а2,… , аn называется число

Среднем геометрическим n положительных чисел

а1, а2,… , аn называется число

2) Для описания точности вычислений применяется

термин погрешность, который является синонимом

слова ошибка. Если точное значение величины равно x,

а вычисленное приближенное значение равно a, то

погрешностью вычисления называется модуль разности

точного и приближенного значений, т. е. число |x - a|

3) а1 * а2 * а3 = R

4) а1 * а2 * а3 = n, но если одно из чисел отрицательно

Ответив на приведенные вопросы, можно сформулировать важное следствие из неравенства о среднем арифметическом и среднем геометрическом: если произведение двух чисел постоянно, то их сумма минимальна, когда эти числа равны друг другу. Это следствие как раз хорошо применимо к сумме, стоящей в скобках знаменателя, т. е. она будет минимальна, когда

Подставив данные задачи, Александр определил, что максимальная полезная мощность, которую можно получить от батареи:

Таким образом, максимальное число лампочек, которые могут гореть полным накалом,

Но как соединить эти 36 лампочек в гирлянду?

Евгений вычислил, какие параметры обеспечивают горение лампочек полным накалом. По известным мощности и напряжению, на которые рассчитаны лампочки, из закона Джоуля - Ленца легко определяется сила электрического тока для полного накала лампочек

Из закона Ома сопротивление нити накаливания лампочки в этом режиме

И теперь надо решить задачу, как нужно соединить лампочки сопротивлением R₀ каждая, чтобы общее сопротивление соединения R₀ было равно r = 10 Ом. Для того чтобы все лампочки горели полным накалом, их положение в электрической схеме соединения должно быть одинаковым.

В общем случае схема соединения лампочек таким образом по казана на рис. 7 : т параллельных групп из п последовательно соединенных лампочек.

Общее сопротивление такого соединения:

Рис. 7 Рис. 8

Из условия R = г с учетом того, что R₀ = 10 Ом, получаем m = n.

Общее число лампочек N = m*n, а мы уже знаем, что N_max = 36, и m = n, тогда m = n = = 6. Таким образом, наиболее эффектная гирлянда получится, если 6 групп из 6 последовательно соединенных лампочек параллельно подключить к батарее.

Возможен и несколько иной способ решения задачи, в котором сразу из приведенных выше общих соображений об обеспечении полного накала всех лампочек рассматривается электрическая схема подключения от параллельных групп из га последовательно соединенных лампочек к батарее (рис. 8).

Далее по правилам Кирхгофа записываются уравнения для токов и напряжений в цепи:

После определения из условий задачи номинальных параметров I₀ и R₀, обеспечивающих полный накал лампочек (что мы уже сделали ранее), получаем, что п и т должны удовлетворять условию:

m + n = 12. (2)

Общее число лампочек N = т*п, и для нахождения максимального значения этого произведения воспользуемся неравенством о среднем арифметическом и среднем геометрическом (по условию (2) сумма чисел m и n постоянна). В итоге получаем m = n = 6 и N_max = 36.

Можно также из условия (2) выразить m = 12 - n и тогда искать максимум квадратичной функции N(n) = 12n - n².

Ответим на следующие вопросы по свойствам квадратичной функции ах² +

bх + с:

1. является ли квадратичная функция монотонной;

2. является ли квадратичная функция ограниченной;

3. при каких значениях коэффициентаа квадратичная функция ограничена снизу, а при каких - сверху;

4. при каких значениях х квадратичная функция принимает экстремальное (минимальное или максимальное) значение?

После ответов на приведенные вопросы очевидно, что функция N(n) имеет максимум и этот максимум достигается при значении п = 6.

Ответы:

1. Нет,не является;

2. Нет, не является;

3. Функция ограниченна снизу при а > 0, ограничена сверху при а < 0;

4. Приx > 0 минимальное, а при x < 0 максимально

ЗАКЛЮЧЕНИЕ.

Умение составлять елочные гирлянды не только интересно, но и познавательно. Тем более, что опрос по теме показал полное незнание этого вопроса. К сожалению, показать все возможности и аспекты составления гирлянд не представляется возможным из-за многообразия видов соединений, множества расчетов и т.д. Однако, опираясь на поставленные задачи, удалось раскрыть суть составления гирлянд, подвести теоретическую базу для грамотного решения данного вопроса. Изначально представлена история появления елочной гирлянды, ее усовершенствование.

Научно - исследовательская работа показала актуальность выбранной темы, ее практическое значение. Успешно решена задача по изготовлению гирлянды с заданными условиями. Необходимо понимать, что процесс составления гирлянды требует не только практических умений, теоретических знаний, но и строгого соблюдения техники безопасности при работе с электричеством.

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Бакалов В.П. и др. Теория электрических цепей. - М.: Радио и связь, 2008.

2. Белецкий А.Ф. Теория линейных электрических цепей. - М.: Радио и связь, 2010.

3. ВалуцэИ.И., "Математика для техникумов", М., 2010;

4. ВиленкинН.Я., "Функции в природе и технике", М., 2008;

5. ГрумбинаА.Б. Электрические машины и источники питания РЭА. Москва, «Энергоатомиздат», 1990

6. Дронов А.М., "Графики функций", М., 2010;

7. Качанов Н. С. и др. Линейные радиотехнические устройства. М.: Воен. издат., 2011

8. Китаев В.Е. Трансформаторы. Москва, «Высшая школа», 2012

9. Колмогоров А.Н., Алгебра и начала анализа 10-11кл., 2014

10. Кушнир И., "Шедевры школьной математики", Киев, 1995;

11. Мордкович А.Г., "Алгебра 9 класс", М., 2002;

12. Мордкович А.Г., "Алгебра и начала анализа 10-11 классы", М., 2014.

13. Н-М журнал, физика в школе №4, 2009г.

14. Попов В.П. Основы теории цепей - М.: Высшая школа, 2010

15. Приложение к газете Первое сентября, 2008. «Производная в физике и технике».

16. СивашинскийИ.Х., "Элементарные функции графики", М., 2012;

17. Сидоров И.Н., Скорняков С.В. Трансформаторы бытовой радиоэлектронной аппаратуры, Москва «Радио и связь», 2011

18. СтолинА.В., "Комплексные упражнения по математике", Харьков, 2012;

ПРИЛОЖЕНИЕ

Вопросы к социологическому опросу.

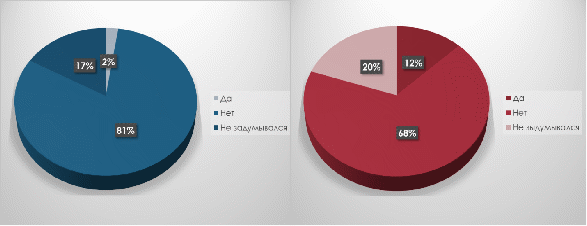
1. Сможете ли Вы самостоятельно собрать елочную электрическую гирлянду? Ответили «Да» -3 человека (2,38%), «Нет» -102 человека (80,95%), «Не задумывался» - 21 человек (16,66%).

2. Знаете ли Вы, из каких дисциплин для этого нужны знания? «Да» - 16 человека (12,69%). «Нет» - 86 человек (68,25%). «Не задумывался» - 25 человек (19, 84%)

Опрошено 126 человек.

Виды электрических гирлянд

Ростовский кремль (18.12.2012, время 19:15)

Ростовский кремль (18.12.2012, время 18:50)

Ростовский кремль (18.12.2012, время 19:30)