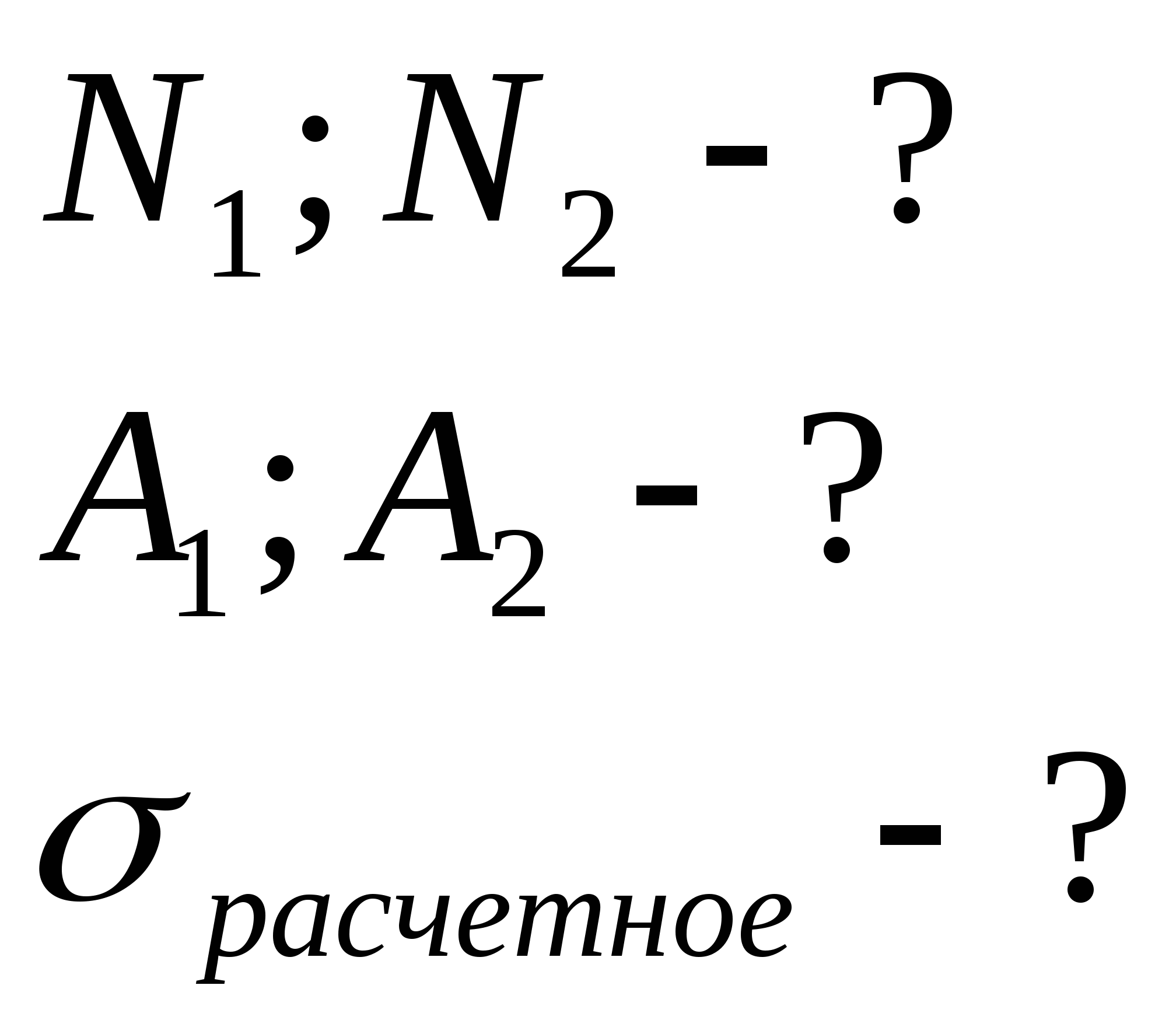- Учителю
- Варианты заданий и методических указаний к выполнению расчетно-графических работ студентами всех специальностей по дисциплине «Сопротивление материалов»
Варианты заданий и методических указаний к выполнению расчетно-графических работ студентами всех специальностей по дисциплине «Сопротивление материалов»
Депобразования и молодежи Югры
бюджетное учреждение профессионального образования
Ханты-Мансийского автономного округа - Югры
«Мегионский политехнический колледж»
(БУ «Мегионский политехнический колледж»)
Преподаватель физики и технической механики
Магомедов А.М.
Варианты заданий и методических указаний
к выполнению расчетно-графических работ
студентами всех специальностей
по дисциплине «Сопротивление материалов»
Методические указания для студентов очной и заочной форм обучения.
Направление: Специальность 131018 Разработка и эксплуатация нефтяных и газовых месторождений.
Мегион,2016
Варианты заданий и методические указания к выполнению расчетно-графических работ предназначены для самостоятельной работы студентов всех специальностей, изучающих курсы сопротивления материалов, прикладной и теоретической механики. Часть 1 методических указаний содержит следующие разделы дисциплины сопротивление материалов: растяжение-сжатие, кручение, изгиб, геометрические характеристики плоских сечений.
Каждая расчетно-графическая работа включает в себя несколько заданий, количество которых определяется преподавателем с учетом числа часов планируемых на самостоятельную работу.
ОБЩИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ
РАСЧЕТНО-ГРАФИЧЕСКИХ РАБОТ
Целью расчетно-графических работ является закрепление теоретического материала по дисциплине, приобретение опыта выполнения расчетов на прочность, жесткость, устойчивость, простых элементов конструкций и навыков в работе с технической литературой, справочниками, стандартами.
Расчетно-графическая работа состоит из нескольких заданий.
Количество заданий, объем каждого, и сроки выполнения определяются кафедрой в соответствии с программой по учебной дисциплине и учебным графиком.
Каждое задание выполняется на бумаге стандартного размера (А4). Титульный лист оформляется на бумаге того же формата по образцу, описанному в приложении 1. Текстовая часть и расчеты должны быть выполнены четко и разборчиво. Чертежи и схемы в текстовой части выполняются в карандаше в соответствии с требованиями Единой системы конструкторской документации.
Схема заданий и числовых данных каждому студенту даются преподавателем в начале изучения курса и распространяются на все задания. В чертежах должны быть проставлены числовые данные соответствующего варианта (не буквенные значения!). Расчеты производить только с числовыми значениями.
Все величины, как в условии задания, так и полученные в результате решения должны содержать их размерность. Решения производить в международной системе единиц (СИ).
Основные обозначения приведены в приложении 3.
ЗАДАНИЕ 1.
ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ
ПЛОСКИХ СЕЧЕНИЙ
Условие и порядок выполнения работы
Для заданного поперечного сечения определить геометрические ха -
рактеристики и построить эллипс инерции.
-
Вычертить в масштабе заданное поперечное сечение балки на стандартном листе формата А4, провести все вспомогательные оси. Выписать из ГОСТов требуемые величины и размеры, привязав их к центральным осям каждой фигуры выполненного чертежа. Основные размеры проставить также на чертеже.
-
Определить положение центра тяжести всей фигуры, применив для этого статические моменты плоских фигур. В качестве вспомогательных осей целесообразно выбрать центральные оси одной из фигур. Провести на чертеже через найденный центр тяжести параллельно прежним осям центральные оси все фигуры.
-
Найти осевые моменты инерции и центробежный момент инерции всей фигуры относительно ее центральных осей.
-
Определить моменты сопротивления фигуры относительно этих центральных осей.
-
Найти положение главных центральных осей фигуры и провести их на чертеже. На чертеже показать также угол поворота главных осей инерции по отношению к прежним осям и его направление.
-
Найти моменты сопротивления фигуры относительно главных центральных осей инерции. При этом расстояние от осей до наиболее удаленных точек фигуры допускается определять графически.
-
Определить радиусы инерции фигуры относительно главных центральных осей и по ним построить эллипс инерции.
-
Исходные данные для решения задания (вариант) берутся из табл. 1.
ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА
В случае замены указанных ГОСТов использовать действующий на момент выполнения РГР.
Таблица 1
РАЗМЕРЫ СТАЛЬНЫХ ПРОФИЛЕЙ
Швеллер, равнополочный,
мм
Швеллер
неравнополочный, мм
1
10
10
10
80×8
75×60×6
80×5×7
80×63×5×7
100×50×5
80×80×40×5
2
10
12
12
90×8
75×60×8
80×6×9
80×63×6×9
100×80×5
90×80×50×4
3
10
14
14
100×8
80×50×6
80×7×9
90×70×6×7
110×50×5
100×80×50×5
4
20
16
16
110×8
90×56×8
100×5×7
90×70×6×9
120×60×6
100×100×60×6
5
20
18
16а
125×8
100×63×8
100×6×9
100×80×6×9
140×60×6
120×60×50×5
6
20
20
18
125×10
125×80×10
120×5×7
100×80×7×9
160×80×6
130×108×50×4
7
20
22
18а
140×10
140×90×10
120×6×9
100×80×8×12
170×70×6
140×70×30×4
8
30
24
20
140×12
160×100×10
160×5×7
120×100×7×9
180×80×6
160×50×30×4
9
30
27
22
160×10
160×100×12
160×6×9
120×100×8×12
180×100×6
160×80×50×5
10
30
30
24
160×12
180×110×10
160×7×9
160×125×8×12
200×100×6
200×50×30×4
Задание 1. Сечения составных балок из стальных профилей
Условия и порядок выполнения работы
Стальной стержень ступенчатого сечения находится под действием внешней силы и собственного веса.
Для определения внутренних усилий разбиваем стержень на отдельные участки, начиная от свободного конца.
Границами участков являются сечения, в которых приложены внешние силы, и место изменения размеров поперечного сечения.Применяя метод сечения, будем оставлять нижнюю часть и отбрасывать верхнюю отсеченную часть стержня.
-
Построить эпюры:
-
нормальных сил
-
нормальных напряжений
-
перемещений поперечных сечений
относительно закрепления.
Площадь большего поперечного сечения стержня в 2 раза превышает меньшую.
Модуль продольной упругости для стали принять равным
E = 2∙105 МПа, удельный вес γ - 78 кН/м3.
-
Исходные данные для решения задания берутся из табл. 2.
Площадь приведена для меньшего поперечного стержня.
Таблица 2
Исходные данные к заданию 2
Задание 2. Схемы нагруженных стержней
СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ СТЕРЖНЕВЫЕ СИСТЕМЫ
Условия и порядок выполнения
Жесткий брус (его деформацией пренебрегаем) шарнирно закреплен с помощью стальных стержней и нагружен сосредоточенной силой F.
Из условия прочности определить площади поперечного сечения стержней. Допускаемое нормальное напряжение для стали принять равным 160 МПа. Толщиной бруса по сравнению с длиной участков и стержней пренебрегаем.
Исходные данные для решения задания берутся из табл. 4.
-
Выполнить заданную схему задачи в карандаше в произвольном масштабе.
-
Показать на этой схеме положение системы после деформирования стержней. Совмещение недеформированной и деформированной систем можно вычертить на отдельном упрощенном рисунке.
-
Составить уравнение совместности стержней. Вычислить реакции из деформаций уравнений совместности и уравнений статики. Найти реакции опор.
-
Сделать проверку.
-
Рассчитать площади поперечного сечения.
-
Рассчитать реальное напряжение.
Таблица 4
Исходные данные к заданию 3
ПЛОСКОЕ НАПРЯЖЕННОЕ СОСТОЯНИЕ
В ТОЧКЕ
Условия и порядок выполнения
-
Вычертить в карандаше в текстовой части заданную схему плоского напряженного состояния в точке. Выписать для своего варианта числовые данные напряжений и проставить их также в чертеже. Знак напряжений соответствует знаку вектора, указанного в схеме.
-
Определить аналитические значения главных нормальных напряжений. Третье главное напряжение в точке, действующее нормально к плоскости чертежа, принять равным нулю.
-
Аналитически определить угол поворота главных площадок по отношению к заданным (этот же угол и между нормалями к прежним и главным площадкам). Затем показать на чертеже положение главных площадок, направления действия главных напряжений и направление угла поворота.
-
Аналитически определить максимальное касательное напряжение в семействе заданных площадок (нормальных к плоскости чертежа), а также максимальное касательное напряжение при данном напряженном состоянии во всем объеме около рассматриваемой точки.
-
Величины, перечисленные в п.п. 2, 3 и 4 определить также графическим путем построения напряжений (кругов Мора).
График должен быть выполнен в масштабе с указанием цифровых величин. Здесь же показать направление действия всех напряжений и угол поворота главных напряжений по отношению к заданным.
-
Определить относительные деформации Ех, Еу и Еz, относительное изменение объема и удельную потенциальную энергию деформации. Коэффициент поперечной деформации для стали принять равным 0,3.
Исходные данные для решения задания (вариант) берутся из табл. 6.
Таблица 6
Исходные данные к задаче 4
Нормальные напряжение, МПа
Касательные
напряжения, МПа
х
у
z
1
10
40
80
20
2
15
45
75
25
3
20
50
70
30
4
25
55
65
35
5
30
60
45
40
6
35
65
40
35
7
40
70
35
30
8
45
75
30
25
9
50
80
25
20
10
55
85
20
15
</
Задача 4. Схемы плоского напряженного состояния в точке
Приложение 1
ОБРАЗЕЦ ТИТУЛЬНОГО ЛИСТА
Депобразования и молодежи Югры
бюджетное учреждение профессионального образования
Ханты-Мансийского автономного округа - Югры
«Мегионский политехнический колледж»
(БУ «Мегионский политехнический колледж»)
Раздел «Сопротивление материалов»
Тема: Геометрические характеристики плоских сечений
Вариант - ___
Выполнил: студент (ФИО)
(подпись, дата)
Проверил: преподаватель (ФИО)
(подпись, дата)
Мегион,2016
Приложение 2
Пример решения задачи 1
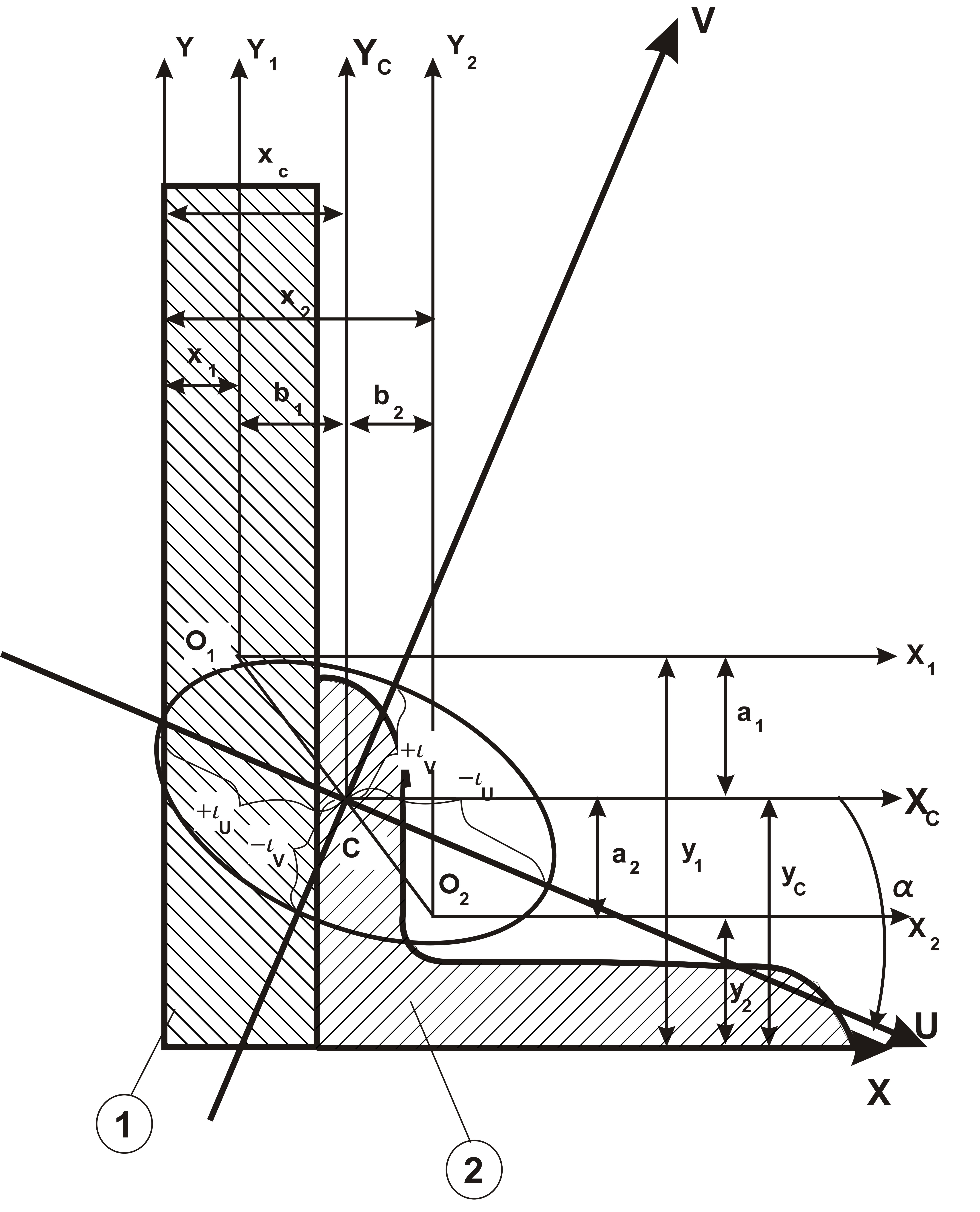
Дано: L
В=14 см, в=9 см, у0=4,58, х0=2,12, Iy=145,54 см4, Ix=444,45 см4, Iu=85,51 см4
Ixy=147 см4, tq=0,409, А=22,24см2
Для прямоугольного сечения: h=2 см, в=15 см, А=30 см2.
-
Определение координат центра тяжести все сложной фигуры (положение центральных осей)
![]() x
x
![]()
![]()
где х1, у1; х2, у2 - расстояние от центра тяжести каждого сортамента до
вспомогательных осей
![]()
![]()
![]()
![]()
2. Определение осевых моментов инерции относительно центральных осей
![]() и
и
![]()
![]()
![]() ,
,
![]() -
расстояние от центра тяжести каждого сортамента до
центральных осей.
-
расстояние от центра тяжести каждого сортамента до
центральных осей.
Откладываем ![]() по оси
по оси ![]()
![]() по
оси
по
оси ![]()
![]()
![]()
![]()
![]()
![]()
![]()
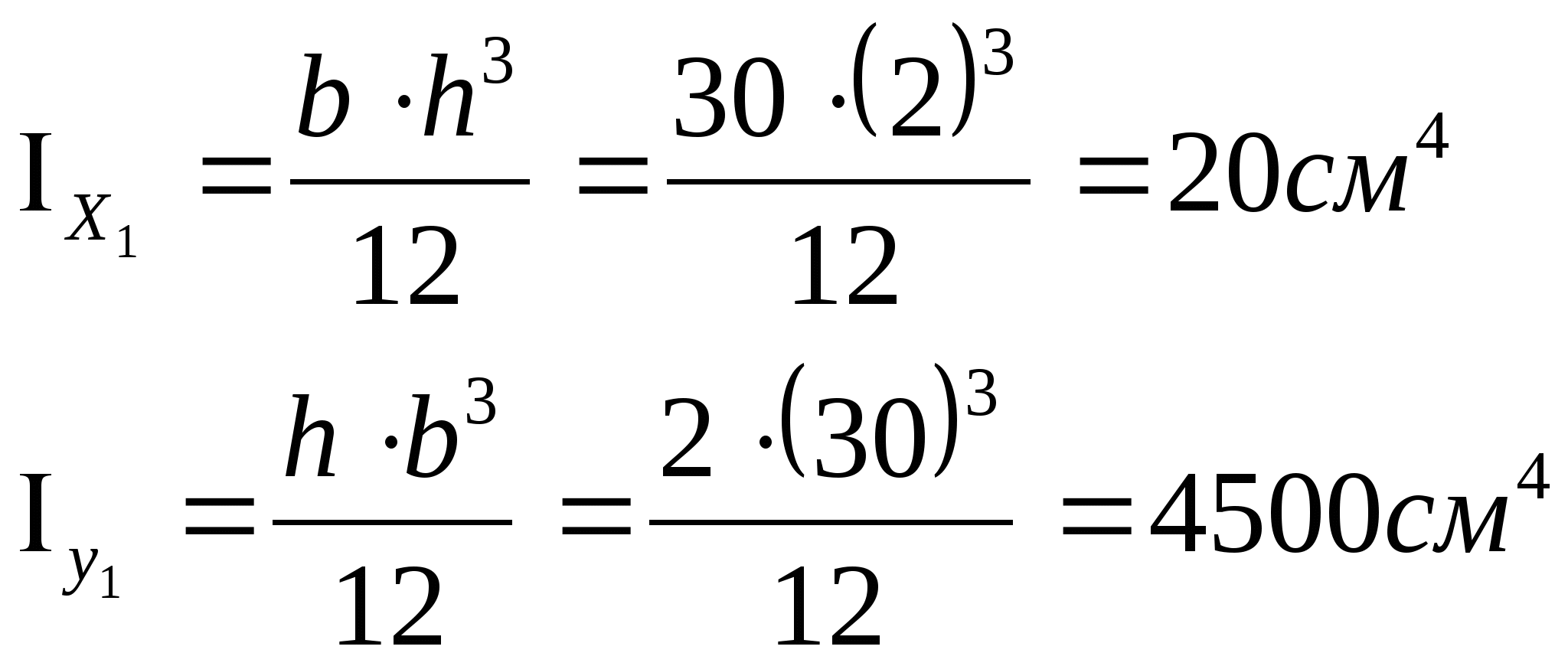
![]()
![]()
3. Определение центробежного момента
инерции относительно центральных осей ![]() и
и ![]() :
:
![]()
![]() ,
т.к. лист имеет горизонтальную ось симметрии, то
собственные центральные оси листа являются главными
,
т.к. лист имеет горизонтальную ось симметрии, то
собственные центральные оси листа являются главными
![]()
![]()
4. Определение моментов сопротивления
относительно центральных осей ![]() и
и ![]() :
:
![]() ;
;
![]() , где
, где
![]() ,
,
![]() - расстояние от центра тяжести всей фигуры до наиболее
удаленных точек по центральным осям
- расстояние от центра тяжести всей фигуры до наиболее
удаленных точек по центральным осям
![]() =
=
![]()
![]() =
=
![]()
![]()
![]()
5. Определение положения главных
центральных осей ![]() угол наклона
угол наклона ![]()
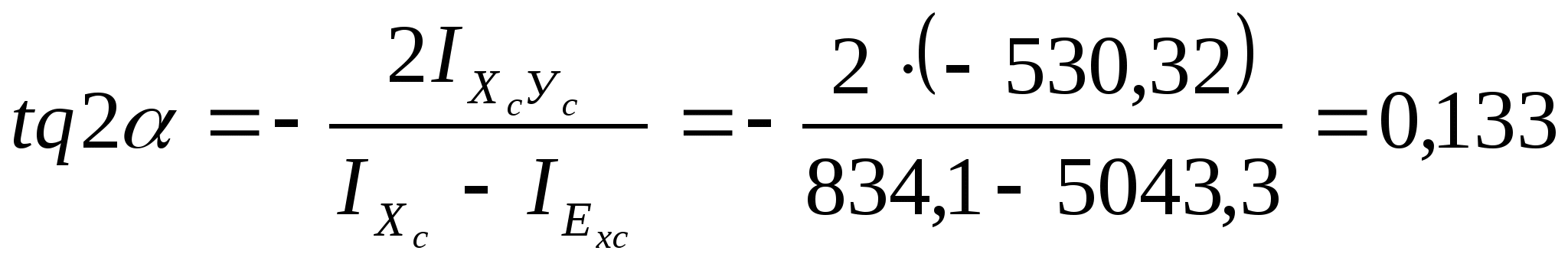
![]() ,
угол откладывается по часовой стрелке
,
угол откладывается по часовой стрелке
Если угол имеет положительное значение, то откладывается против часовой стрелки.
6. Определение главных центральных моментов инерции относительно главных центральных осей:
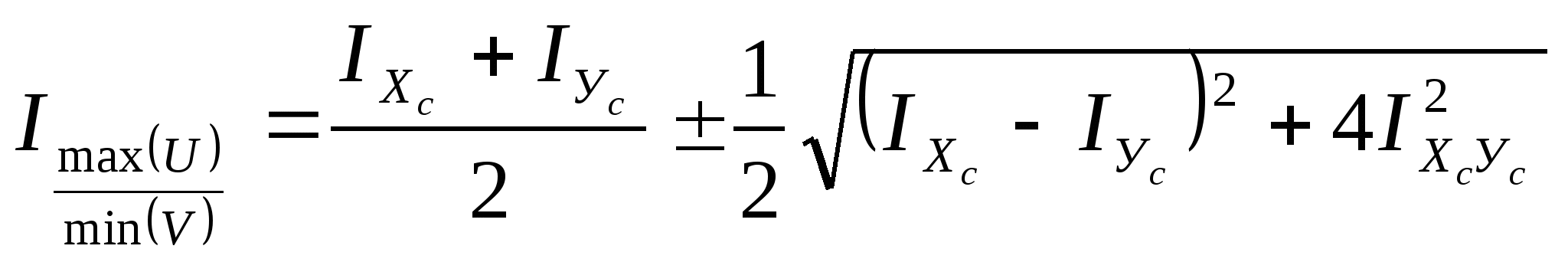
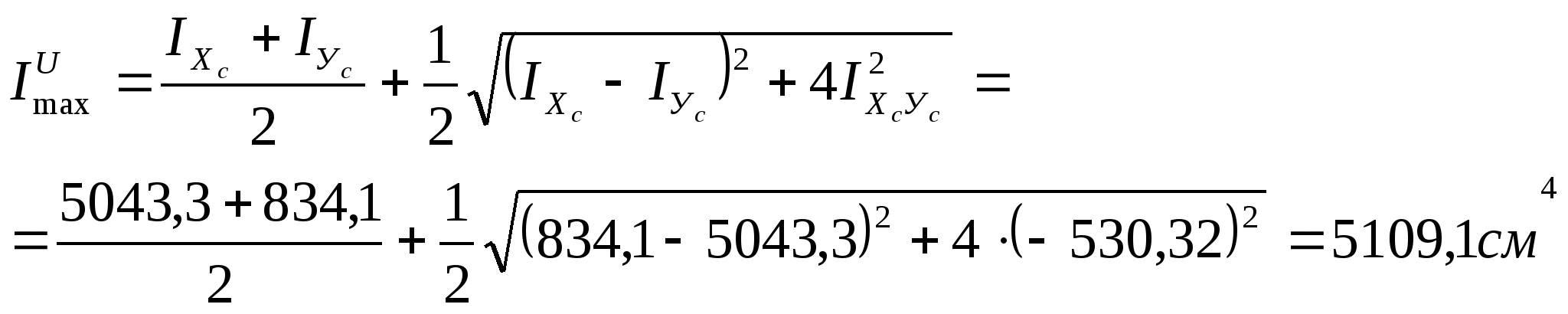
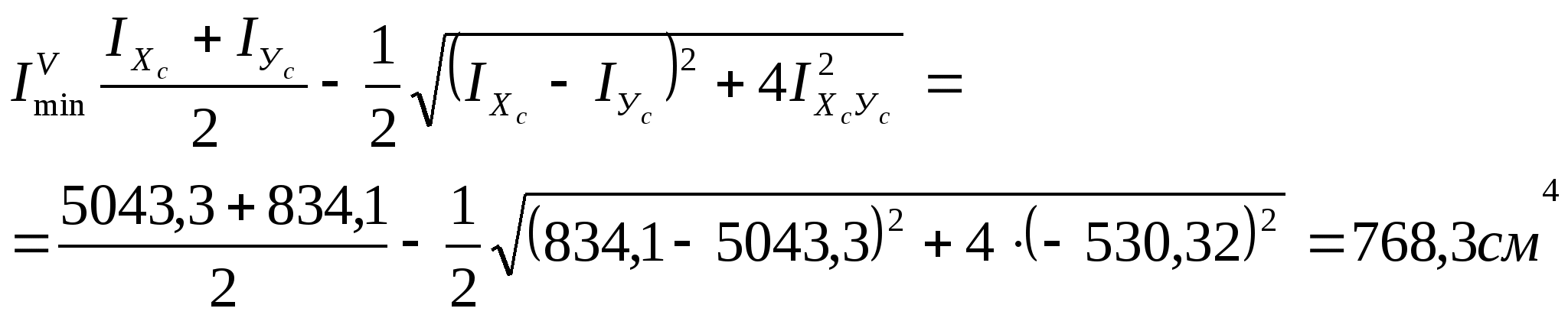
7. Определение моментов сопротивления
относительно главных центральных осей ![]() :
:
![]()
![]()
8. Определение радиусов инерции
![]() относительно центра тяжести:
относительно центра тяжести:
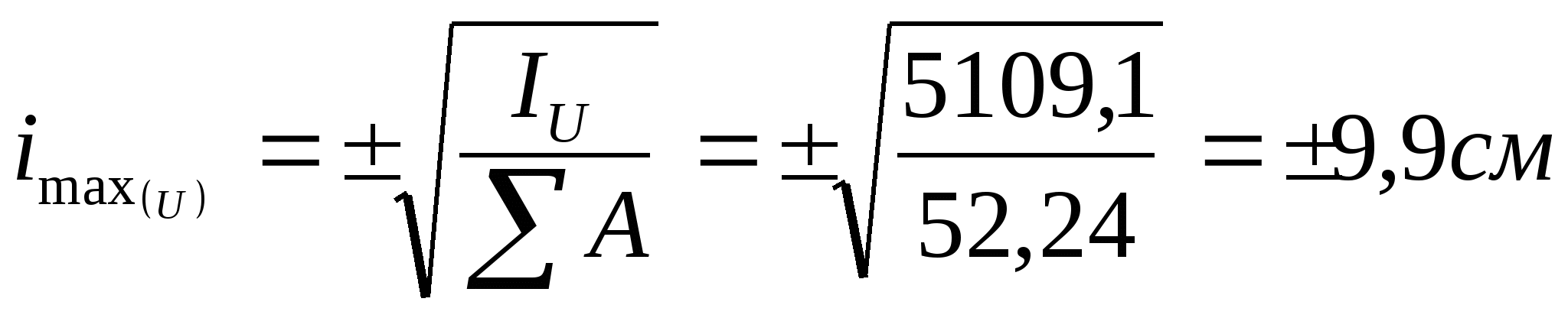
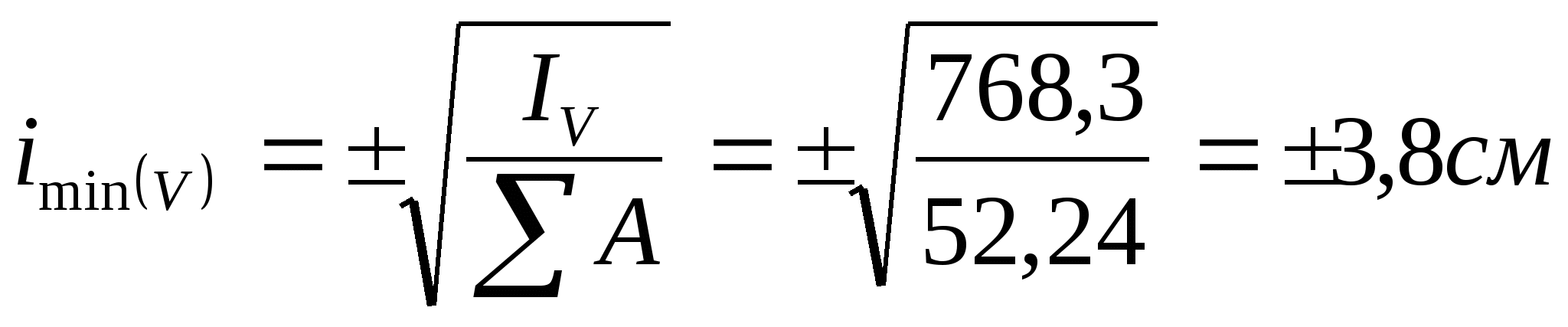
9. Проверка:
![]()
834,1+5043,3=5109,1+768,3
5877,4=5877,4(см4)
Пример решения задачи 2
-
Для определения внутренних усилий разбиваем стержень на отдельные участки, начиная от свободного конца.
Границами участков являются сечения, в которых приложены внешние силы, и место изменения размеров поперечного сечения. Таким образом, заданный стержень имеет два участка.
Применяя метод сечения, будем оставлять нижнюю часть и отбрасывать верхнюю отсеченную часть стержня.
-
Определение реакции опоры
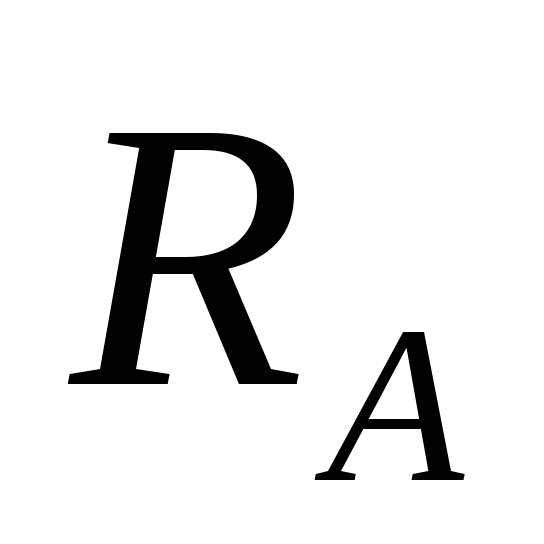 в жесткой заделке в т.А:
в жесткой заделке в т.А:
![]()
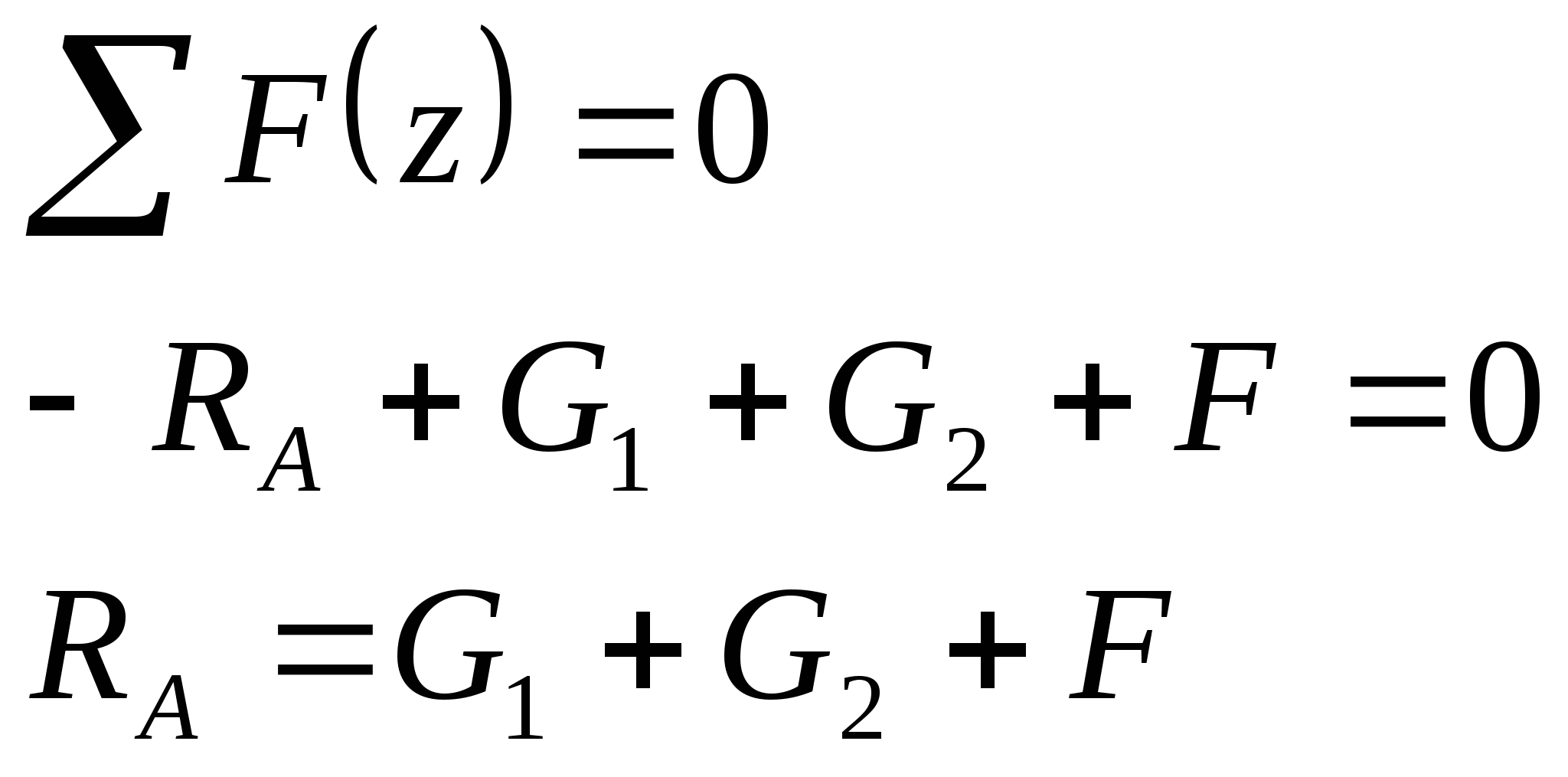
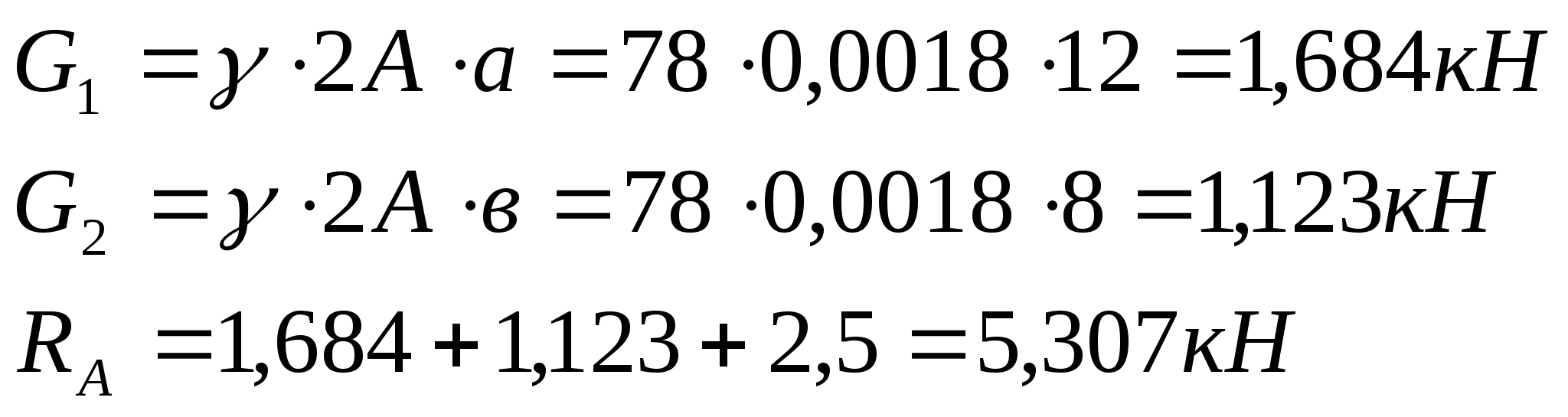
-
Определение продольной силы
 в сечениях стержня методом сечения
в сечениях стержня методом сечения
Проведем произвольное сечение на участке I-I.
Сечение I-I
Построим эпюру, показывающую как меняется, ![]() по длине стержня. Для этого, проведя ось абсцисс графика
параллельно оси стержня, откладываем в произвольном
масштабе значения продольных сил по оси ординат. Полученный
график принято штриховать, при этом штриховка должна быть
перпендикулярна оси стержня.
по длине стержня. Для этого, проведя ось абсцисс графика
параллельно оси стержня, откладываем в произвольном
масштабе значения продольных сил по оси ординат. Полученный
график принято штриховать, при этом штриховка должна быть
перпендикулярна оси стержня.
-
Определение нормальных напряжений
 , возникающих в сечениях стержня:
, возникающих в сечениях стержня:
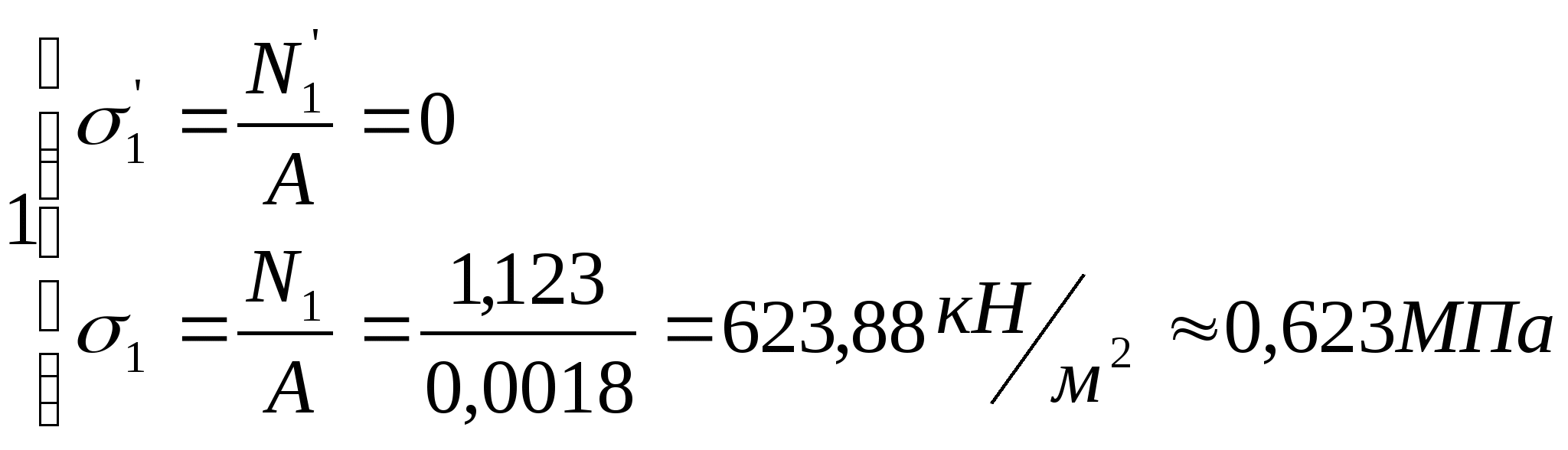
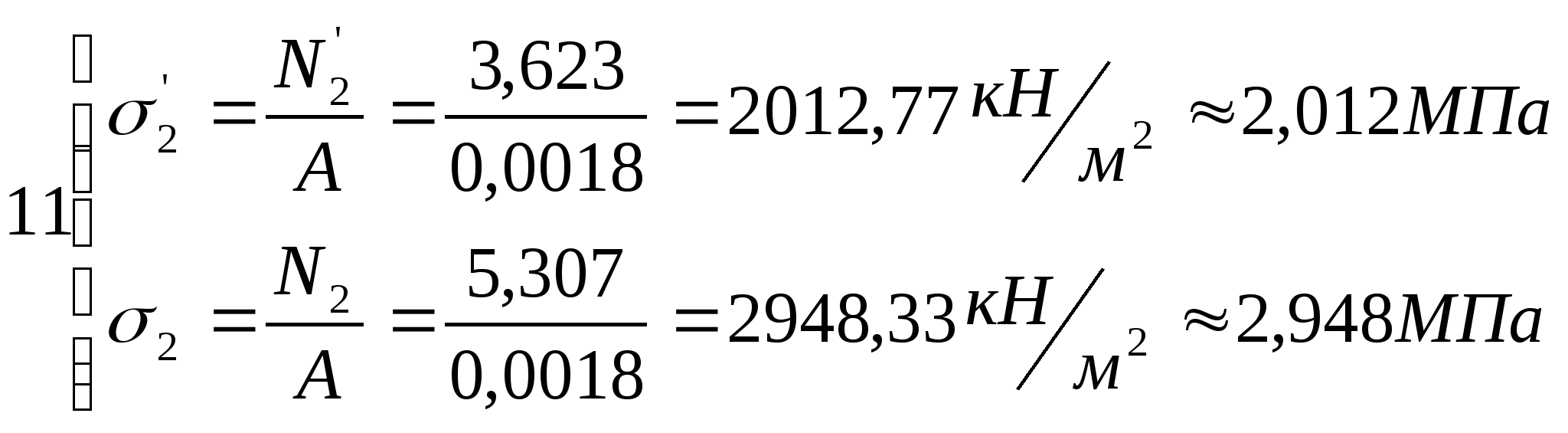
-
Определение удлинения (перемещения)
 сечений после деформации:
сечений после деформации:
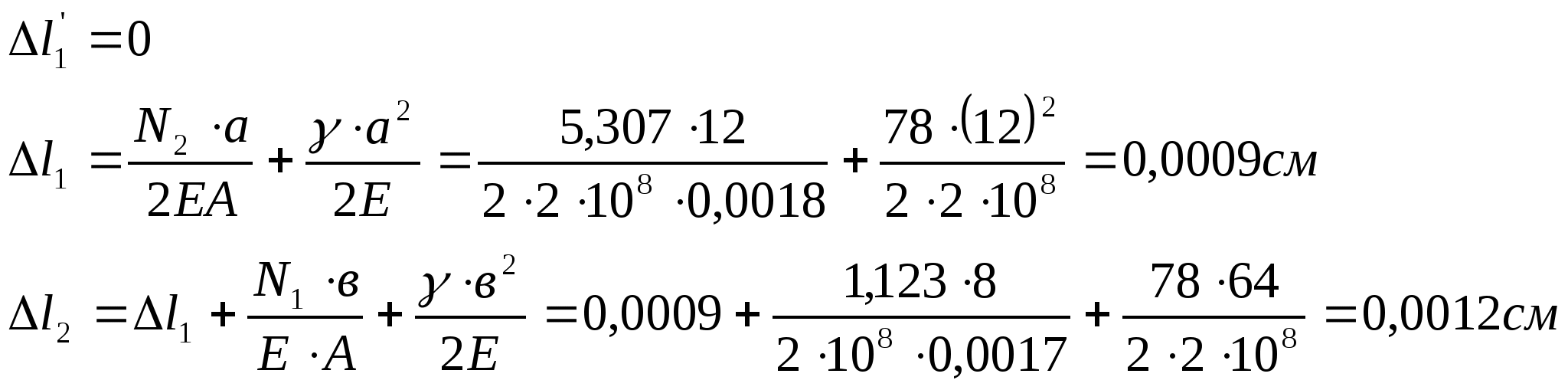
Эпюру перемещений следует строить от защемленного конца
-
Определение погрешности
![]()
![]()
![]()
П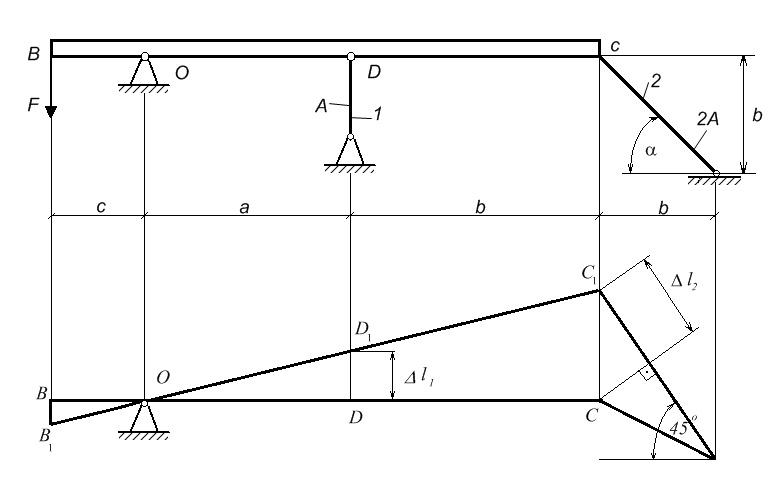
ример решения задачи 3
|
Определить:
|
1. ![]() l1 - удлинение стержня 1
l1 - удлинение стержня 1
l2 - удлинение стержня 2
Из подобия треугольников ОДД1 и ОСС1
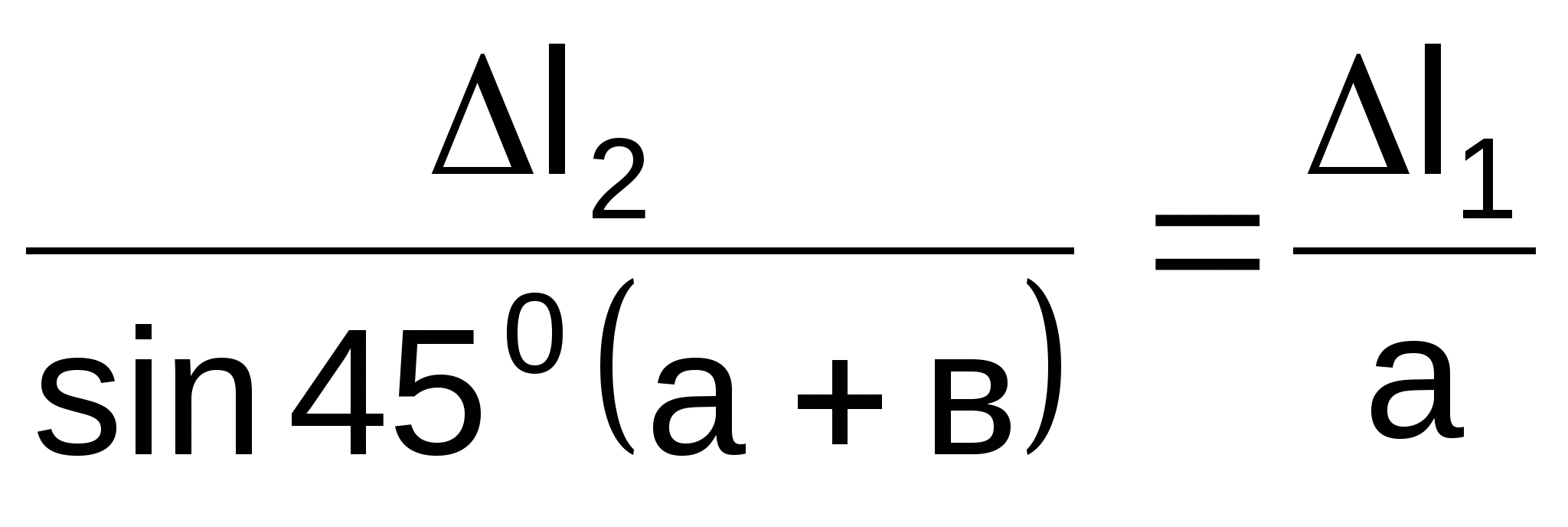
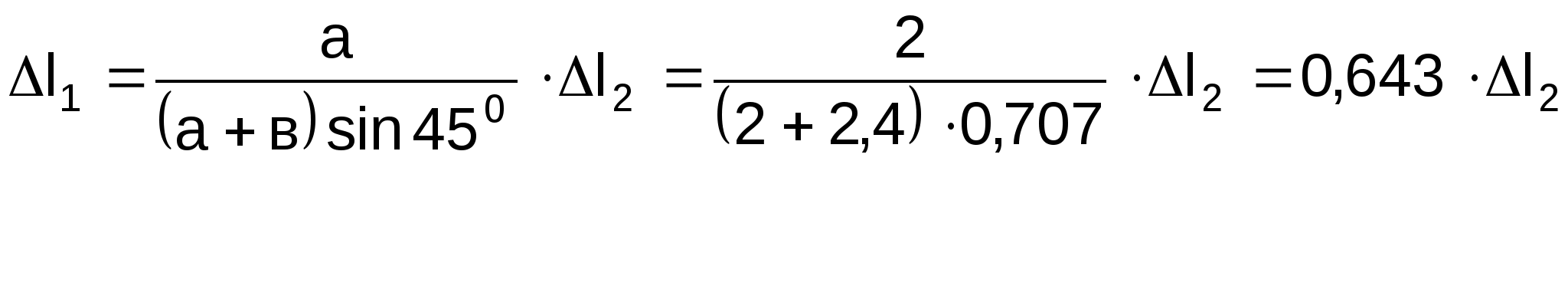
![]() -
уравнение совместности деформаций стержней. (1)
-
уравнение совместности деформаций стержней. (1)
По закону Гука удлинения стержней определяются:
![]()
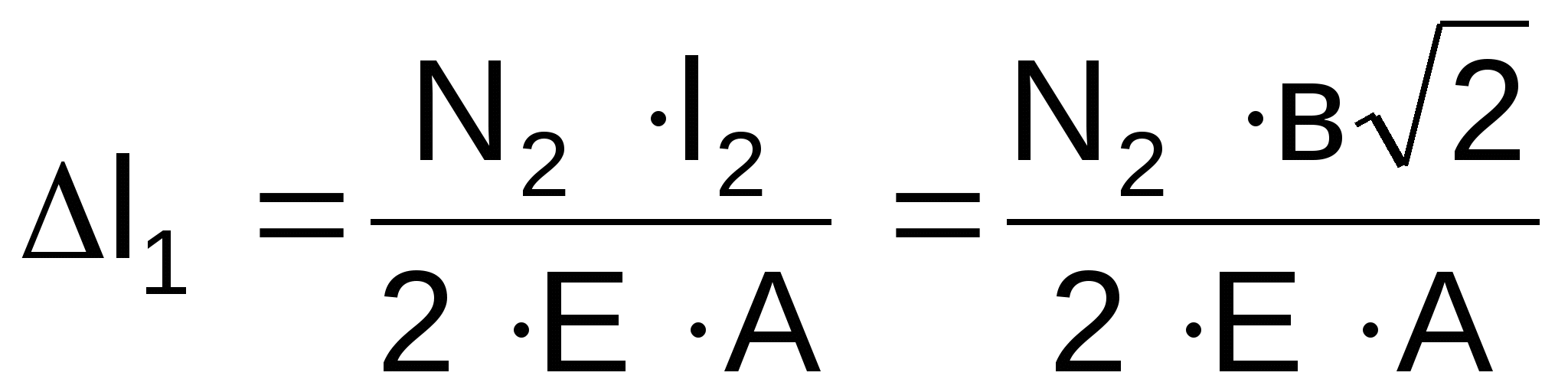
Выполним подстановки в уравнение (1), получим:
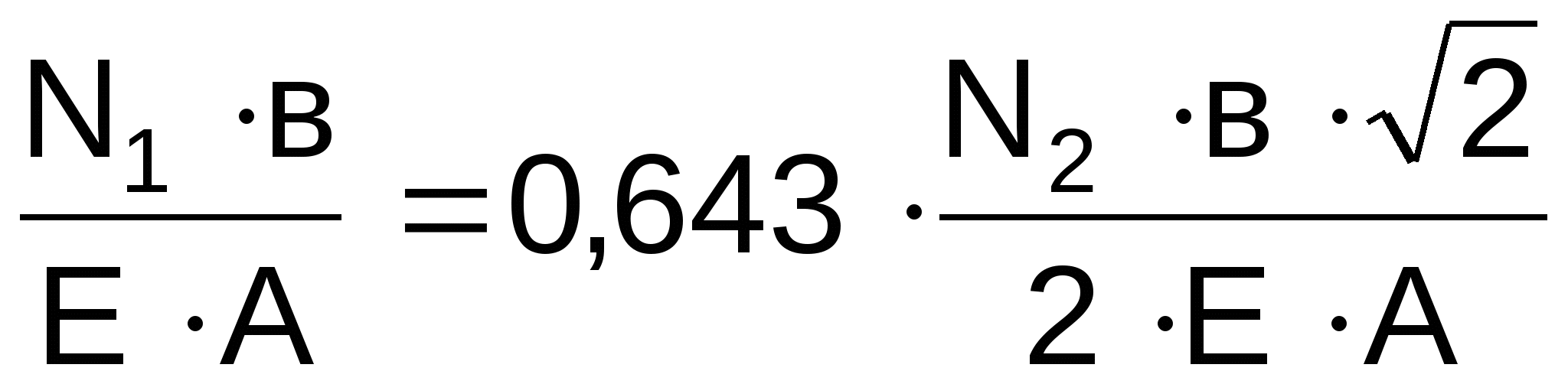 ,
откуда
,
откуда
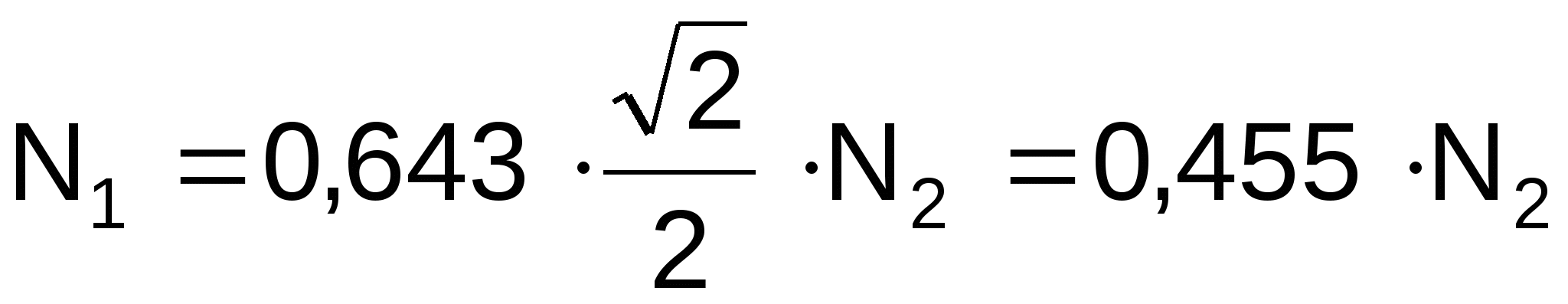 (2)
(2)
Заменим стержни 1 и 2 их реакциями
(![]() ).
).
Составим уравнение статики:
![]()
![]()
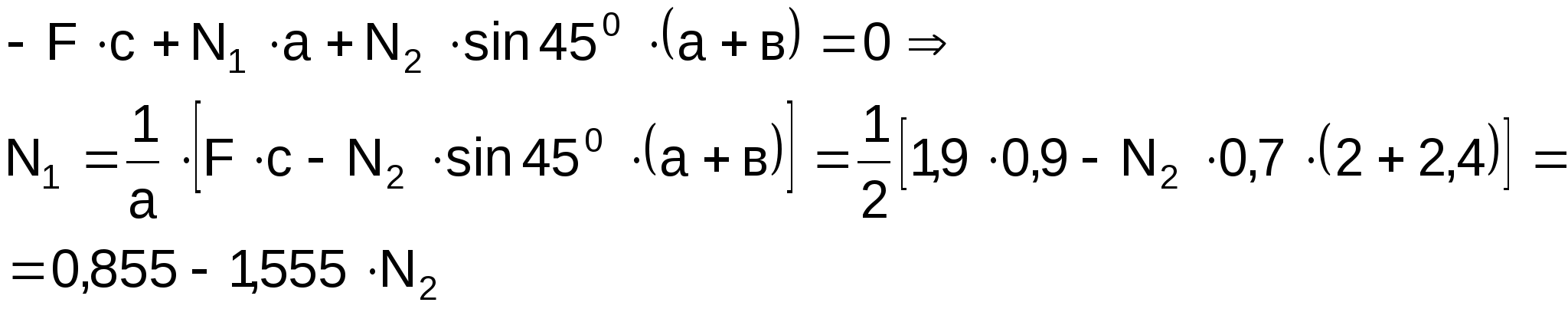
Выполним подстановку в уравнение (2):
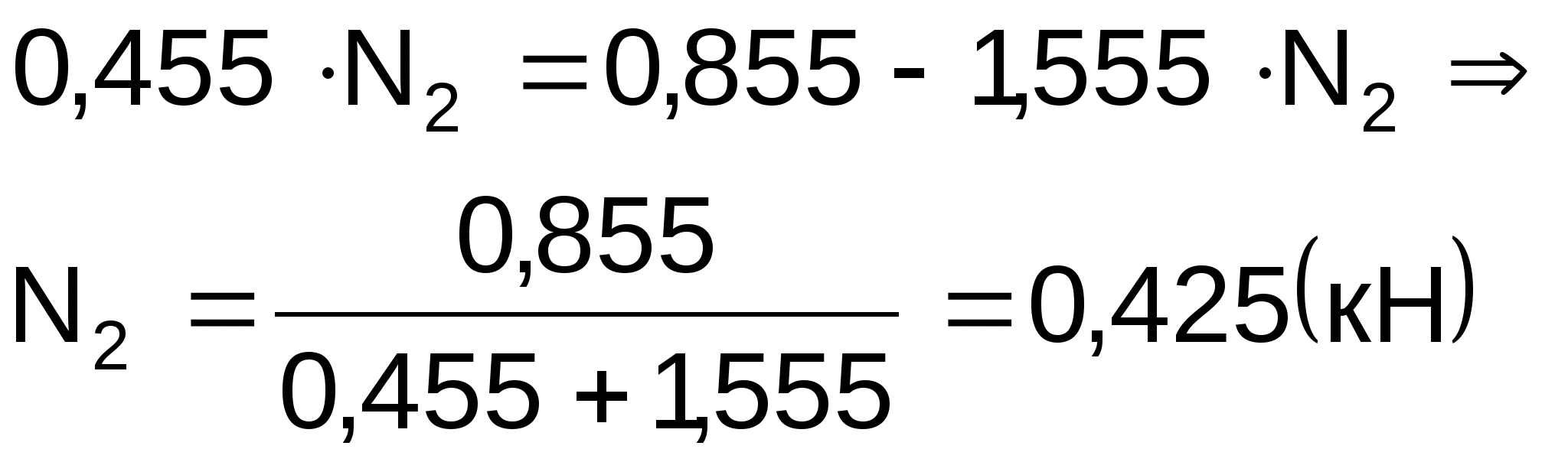
![]()
![]()
![]()
Проверка вычислений производим подстановкой в уравнения статики:
![]()
![]()
Расчет верен.
Расчет площади поперечного сечения стержня (№ 2):
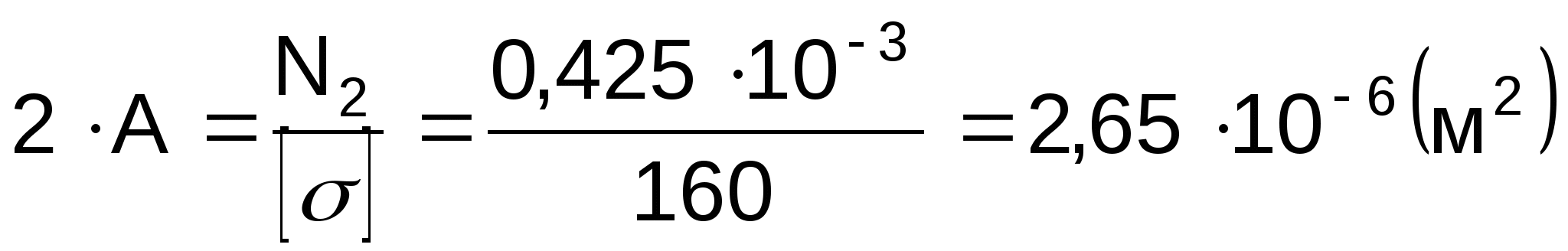
Расчет площади поперечного сечения стержня (№1):
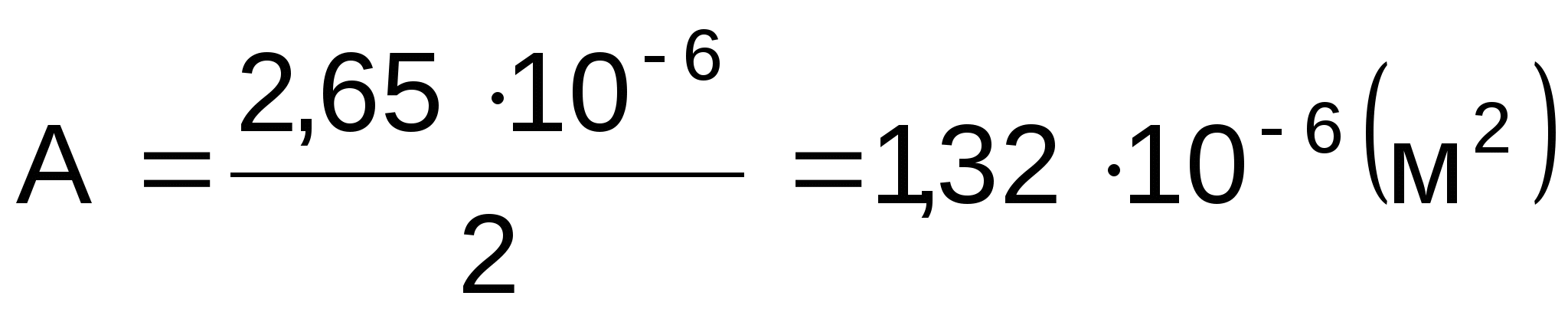
Расчет нормального напряжения в стержне (№1):
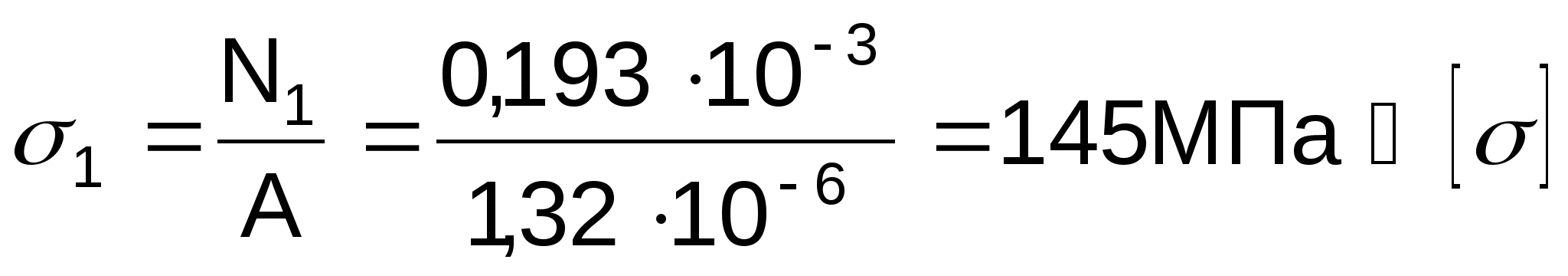 ,
т.е. 160 МПа - что допустимо.
,
т.е. 160 МПа - что допустимо.
Прочность обеспечена!
Пример решения задачи 4
Для данной схемы плоского напряженного состояния в элементе детали необходимо определить:
-
Главные напряжения и положение главных площадок.
-
Максимальное касательное напряжение.
-
Относительные деформации.
-
Удельную потенциальную энергию деформации.
Материал детали - сталь.
После определения главных площадок и главных напряжений их поло
жение и направление действия - нанести на заданную схему.
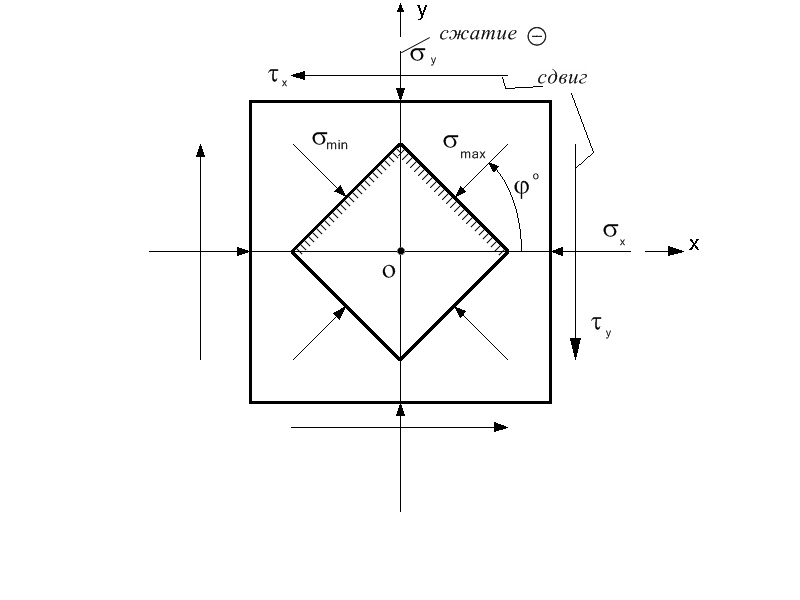
-
Определение главных площадок и главных напряжений:
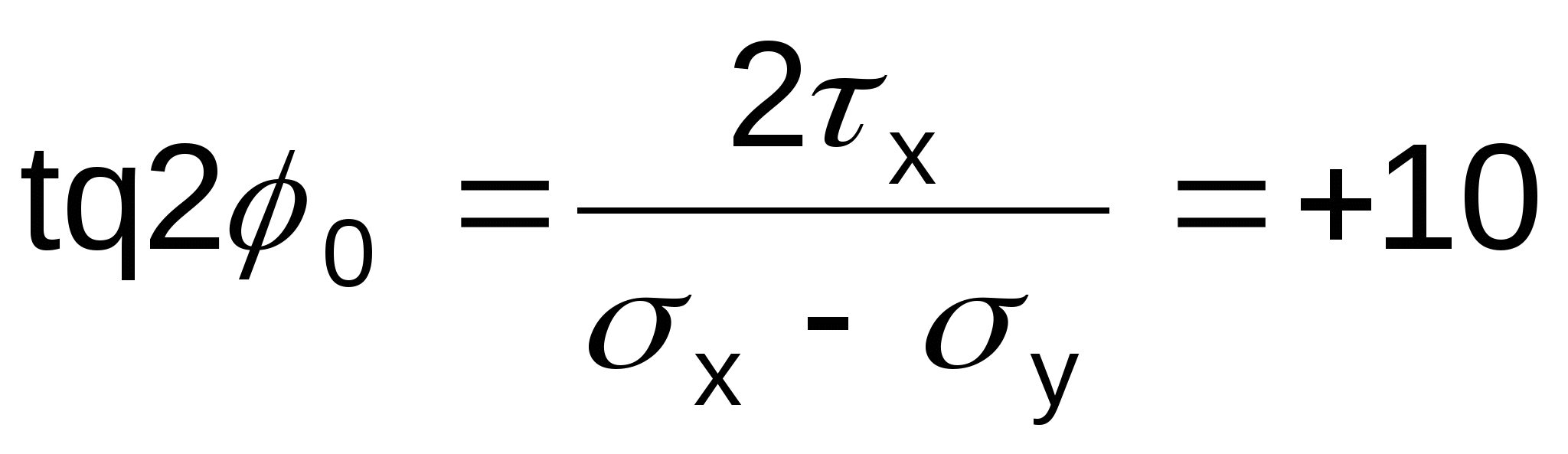
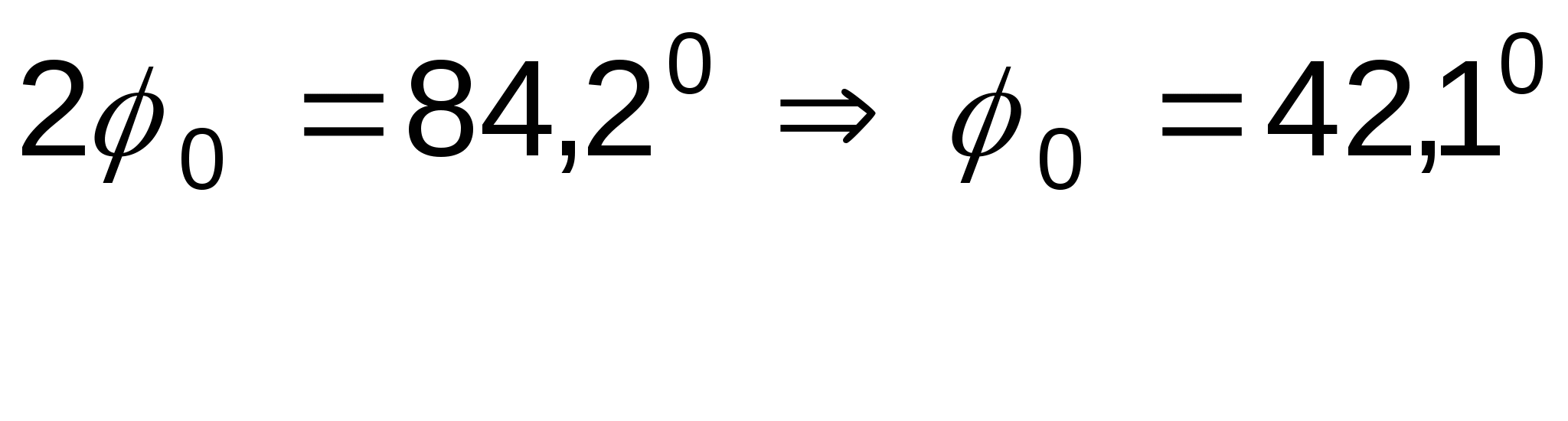
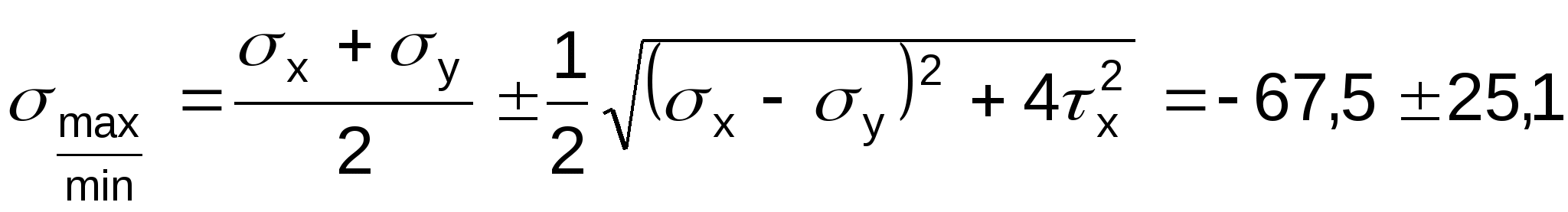
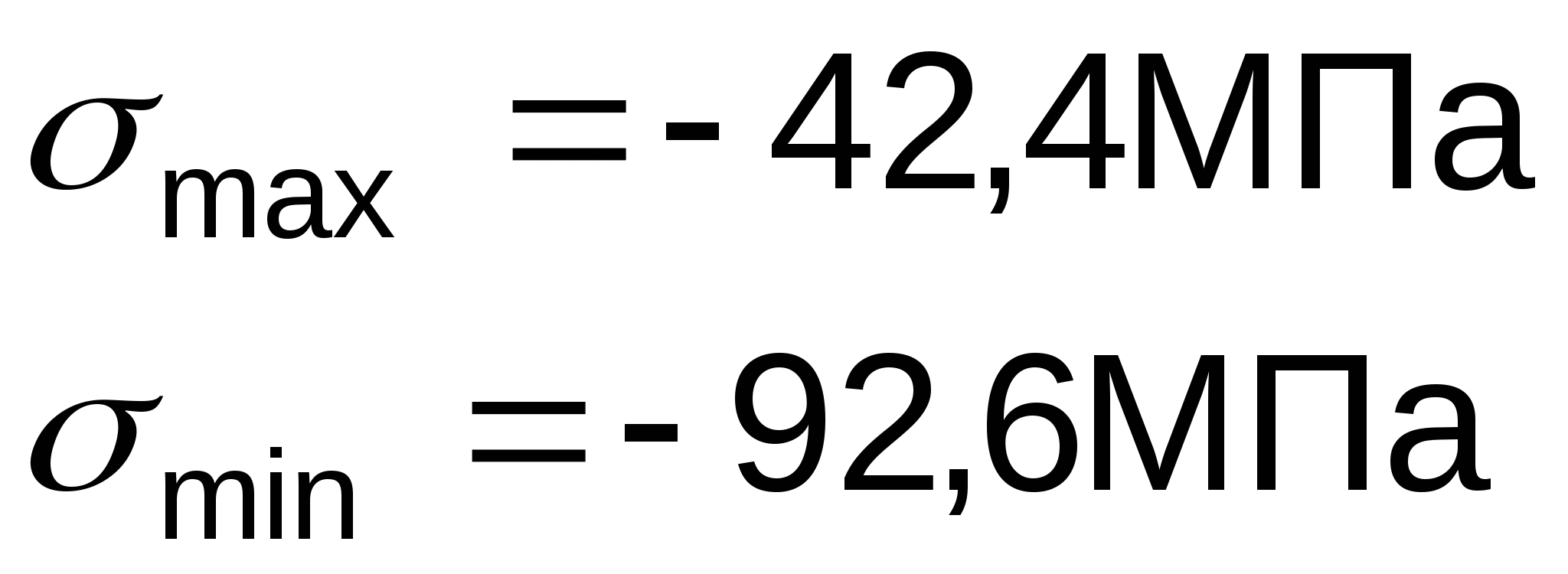
Максимальные касательные напряжения равны:
![]()
-
Относительные деформации заданной площадки определяются:
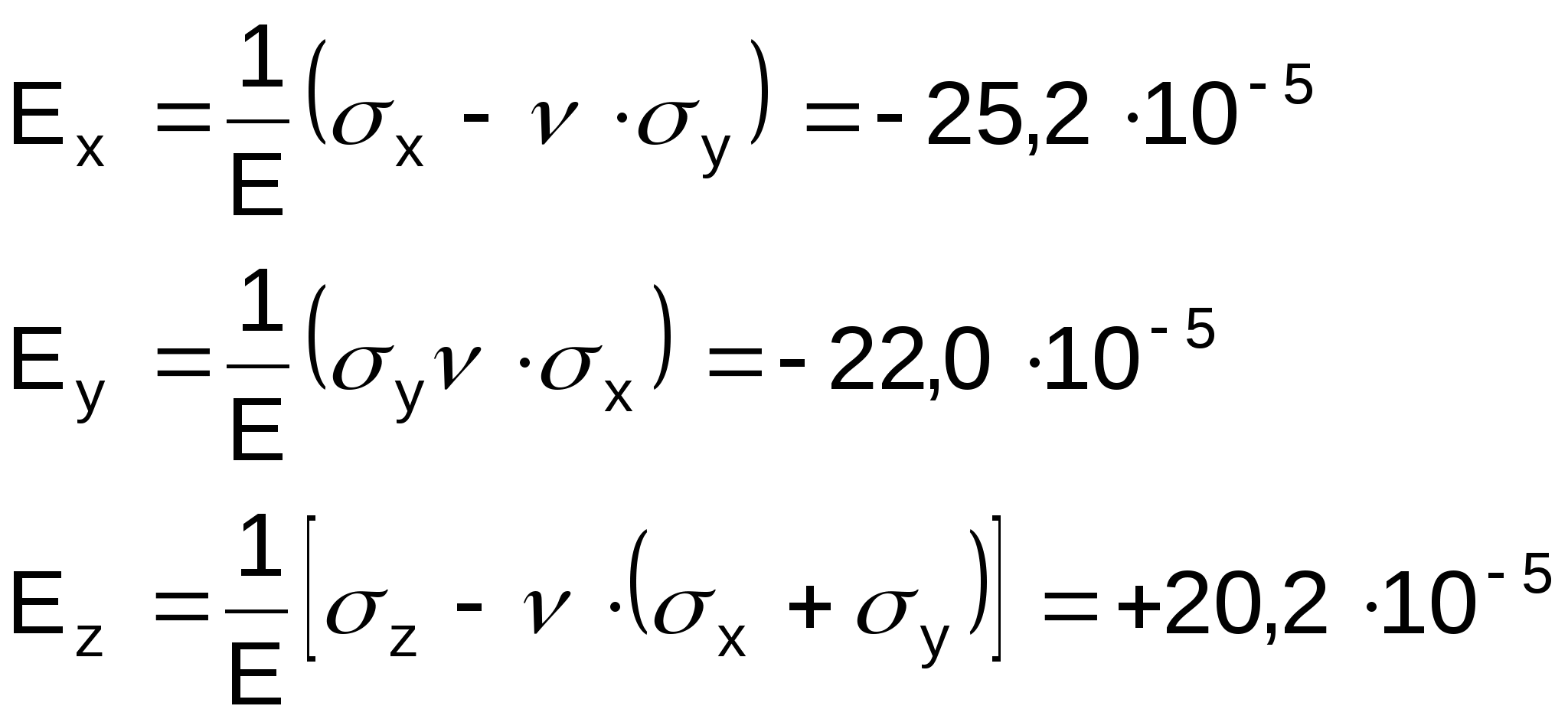
-
Удельная потенциальная энергия деформации заданной площадки:
![]()
-
Проверка вычислений:
![]()
![]()
ОСНОВНЫЕ ОБОЗНАЧЕНИЯ
Система СИ
F - сосредоточенная сила (условно как бы приложенная в одной точке);
q - интенсивность распределенной нагрузки, сила на единицу длины (Н/м, МН/м);
М - внешний момент, действующий на элемент конструкции (изгибающий или крутящий);
- удельный вес материала;
- нормальное напряжение (сигма );
- касательное напряжение (тау );
- допускаемое нормальное напряжение;
р - допускаемое нормальное напряжение при растяжении;
сж - допускаемое нормальное напряжение при сжатии;
- допускаемое касательное напряжение (0,5…0,6);
1, 2, 3 - главные напряжения (экстремальные нормальные);
max, max - максимальные напряжения;
а, a - напряжения по произвольной наклонной площадке;
n, nу - коэффициенты запаса прочности и устойчивости;
N - продольная сила;
Qx, Qy - поперечные силы;
Мх, Му - изгибающие моменты относительно осе Х и У;
Мкр - крутящий момент (относительно продольной оси Z);
Е - модуль упругости Юнга для широкого круга материалов (Е = 2∙105 МПа);
G - модуль сдвига (G=8104 МПа);
- коэффициент Пуассона;
- предел текучести;
в - предел прочности;
пп - предел пропорциональности;
Sк - истинное сопротивление разрыву;
- относительное продольное удлинение;
- относительное поперечное сужение;
u - удельная потенциальная энергия деформации;
W - работа внешней силы;
ху, zx, уz - угловые сдвиговые деформации в разных плоскостях;
l - абсолютное продольное удлинение (или укорочение);
1, 2, 3 - главные относительные деформации;
- относительное продольное удлинение (или укорочение);
- угол закручивания поперечного сечения вала при кручении;
d - диаметр круглого стержня;
у - прогиб балки при изгибе;
z - координата произвольной точки сечения при рассечении по методу РОЗУ;
Sх, Sу - статические моменты площади сечения относительно осей Х и У;
А - площадь поперечного сечения стержней, балок и валов;
А0 - первоначальная (до нагружения) площадь поперечного сечения образца растяжения;
хс, ус - координаты центра тяжести сечения;
хi, уi - координаты центров тяжести отдельных фигур сечения;
Ix, Iy - относительные моменты инерции относительно осей Х и У;
Iху - центробежный момент инерции сечения относительно осей Х и У;
IР - полярный момент инерции сечения относительно координат;
iх, iу - главные радиусы инерции;
Imax,Imin - главные моменты инерции сечения;
Wх, Wу - осевые моменты сопротивления сечения (использются при расчете на прочность при изгибе)
WР - полярный момент сопротивления сечения (используется при расчете на кручение);
1 МПа = 1000 кН/м2
1 кН = 100 кг
Е = 2105 МПа = 2108 кН/м2
= 160 МПа = 160000 кН/м2
А = 2 см2 = 0,0002 м2