- Учителю
- Комплекс учебных пособий Физика - 7 класс Учебник
Комплекс учебных пособий Физика - 7 класс Учебник


Требования к учащимся на уроках физики.
1. Требования к тетрадям.
На уроках физики достаточно иметь две тетради.
а) Рабочая тетрадь - 48 листов в клетку: для выполнения записей на уроке и для выполнения домашних работ. На каждом уроке перед объяснением нового материала надо записать Тему урока и на полях дату, например, 03.09.14. В этой же тетради оформляются письменные Домашние работы.
б) Проверочная тетрадь - 18 листов в клетку: для выполнения Тестов после каждой темы, для оформления Лабораторных и Контрольных работ. Эта тетрадь хранится у учителя и выдаётся учащимся только на уроке для выполнения нужной работы. Для проведения этих работ прилагается Сборник тестов. Из сборника надо переписать Заголовок работы, на полях - дату.
Ученик должен выполнить сначала Домашнюю работу, а потом на следующем уроке аналогичный Тест. Если ученик успешно выполнил Тест, то учитель может Домашнюю работу не проверять. Если ученик на уроке с Тестом не справился, то учитель проверяет Домашнюю работу и может после урока дать дополнительный Тест на оценку "3".
Корочка Проверочной тетради оформляется таким образом:
Задание на уроке:
1. Подпишите проверочную тетрадь (18 листов, в клетку) и сдайте её учителю.
2. Подпишите произвольно рабочую тетрадь (48 листов, в клетку) и запишите Тему 1.
ТЕТРАДЬ
для проверочных работ
по физике
ученика 7 класса
Гауфской школы
Фамилия
Имя (полное).
2. Требования к знаниям.
По каждой теме ученик должен сдать Тест - хотя бы обязательную часть. Для этого он должен выучить и написать Определения (законы, правила), которые оформлены в данной книжке в рамочках, а также выучить формулу для решения задачи, понимать все буквы в формуле и уметь превращать единицы измерения в систему СИ. Иначе ученик не может успевать в четверти!
На оценку "4" ученик должен свободно решать основные качественные задачи теста, уметь выразить любую букву из формулы вычислительной задачи, уметь находить недостающие данные из таблиц, выполнять приближённые вычисления и округлять ответ. Ученик должен понимать теорию из данной книжки и уметь воспроизвести решённые в ней задачи.
На оценку "5" ученик должен уметь решать новые качественные и количественные задачи, которые не были "отрепетированы" на уроке, причём уметь выводить расчётные формулы для решения задач в два действия. Кроме того, ученик должен дома читать параграф учебника и уметь при тестировании ответить на простые вопросы по прочитанному в учебнике.
На оценки "4" и "5" надо уметь решать задачи на давно пройденный материал, которые будут попадаться в Тестовых и тем более в Контрольных заданиях.
3. При выполнении Тестов обратите внимание:
1. Обязательно перепишите Заголовок и поставьте на полях Дату.
2. Из тестов в Проверочную тетрадь переписывайте только жирный шрифт.
3. Обязательно ставьте у заданий номера (1. 2. 3.) и буквы а), б), в).
Тема 1. Что изучает физика? §1 и §3
1. Откуда пришло слово "физика"? Какие науки изучают природу?
Слово "физика" в переводе с греческого означает "природа" (Аристотель). В русский язык слово "физика" ввёл Михаил Васильевич Ломоносов. Природу изучают науки: физика, химия, биология, география, геология, астрономия.
2. Что изучает физика? Какие бывают явления природы?
Физика изучает физические явления природы. Физические явления бывают:
механические (движение тел: падение камня, вращение колеса);
тепловые (плавление льда, испарение воды, нагревание утюга);
электромагнитные (электрический ток, притяжение железа к магниту);
звуковые (гром, музыка); световые (молния, свет лампы).
Каждый раздел физики изучает свой круг явлений. Например, раздел физики механика изучает механические явления, теплота изучает тепловые явления, оптика изучает световые явления, акустика изучает звуковые явления, электричество изучает электрические явления и т.д.
3. Зачем физика изучает явления природы?
Физика изучает физические явления природы, чтобы понять, как они происходят и почему происходят, чтобы потом использовать эти знания. Например, итальянский учёный Галилео Галилей изучал, как падают с одинаковой высоты маленький и большой камни, и открыл закон, что они падают на землю одновременно. Позднее английский учёный Исаак Ньютон выяснил, почему камни падают на землю, и понял, что это происходит из-за притяжения Земли.
Оба учёных открыли законы физики: Галилей открыл закон свободного падения тел, а Ньютон - закон всемирного тяготения. Законы физики всегда остаются верными и никогда не нарушаются, сколько бы раз явление не повторялось. Законы физики открывают, чтобы люди использовали их на практике.
4. Какие два способа изучения природы используются в физике?
Физические явления изучают с помощью наблюдений и опытов. Чаще всего физики проводят в своих лабораториях опыты, чтобы изучать явления. Но, например, извержение вулкана или затмение Солнца ученые могут только наблюдать в природе.
Во время наблюдений и опытов учёные проводят измерения. На основе измеренных данных учёные сперва выдвигают гипотезу (предположение), почему данное явление происходит именно таким образом, а не иначе. Со временем, когда данных становится больше, открывают новый закон физики.
Дома: 1. Прочитайте §1 и §3 и сумейте ответить на какой-нибудь вопрос по этим параграфам. Например, какой опыт проводил Галилей в городе Пиза?
2. Изучите Тему 1 по данной книжке. Умейте ответить на вопросы:
а) Как переводится слово "физика"? Кто предложил впервые этот термин? Кто ввёл этот термин в русский язык?
б) Что изучает физика? К каждой группе физических явлений приведи пример.
в) Как называются самые важные открытия в физике? Какой закон открыл Галилео Галилей? Кто открыл закон всемирного тяготения?
г) Какими двумя способами учёные открывают законы физики?
Тема 2. Тело, вещество, материя. §2 и §8
1. Что такое физическое тело и что такое вещество? §2
Опр. Физическим телом наз. любой предмет в окружающем мире.
Примеры физических тел: камень, лист бумаги, песчинка, Луна, капелька воды, вода в бутылке, кусок льда, человек.
Каждое тело имеет свою форму и определённый объём. Каждое тело состоит из вещества или из смеси разных веществ. Вещество состоит из молекул, а молекулы состоят из атомов.
Опр. Веществом наз. то, из чего состоят физические тела.
Примеры: камень состоит из вещества гранит, лист бумаги состоит из вещества бумага, капелька воды, вода в бутылке и кусок льда - все эти три тела состоят из вещества вода, гвоздь состоит из вещества железо. Человек состоит из огромного количества разных веществ.
Опр. Вселенной наз. весь окружающий мир. Материей наз. всё, что на самом деле есть во Вселенной. Материя бывает двух видов: вещество и поле.
Все тела во Вселенной состоят из вещества. Но кроме тел есть ещё радиоволны, свет, магнитное поле, которые являются полями и не состоят из атомов.
2. Вещество состоит из молекул и атомов. §8
Древнегреческий учёный Демокрит 2 500 лет назад высказал мысль, что вещества не сплошные, как нам кажется, а состоят из мельчайших частиц.
Древние греки лишь догадывались, что вещества состоят из частиц, но у них не было доказательств. Современная химия доказала, что вещества состоят из молекул, а молекулы состоят из атомов. Наиболее крупные молекулы удалось даже сфотографировать через электронный микроскоп. Химикам известно строение молекул миллионов веществ. Например, молекула воды состоит из одного атома кислорода О и двух атомов водорода, поэтому формулу воды пишут Н2О (аш-два-о). Разных атомов в природе не так уж много - около сотни (таблица Менделеева), но из них строятся молекулы миллионов разных веществ, как из букв слова.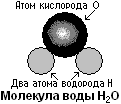
Некоторые вещества состоят прямо из атомов - нет молекул. Например, железный гвоздь состоит прямо из атомов железа, уголь - из атомов углерода.

3. Молекулы очень маленькие.
Вещество кажется нам сплошным, потому что молекулы очень малы и не видны в обычный микроскоп. В 1 см3 воздуха содержится такое огромное число молекул, что если в каждую секунду оттуда выпускать по миллиону молекул, то молекул хватило бы почти на миллион лет.
То, что молекулы малы, подробнее описано в учебнике §8, стр.19 (про ниточку из молекул воды, про плёнку из капли масла, про крупинку соли).
Дома: 1. Выучите все три определения в рамочках из Темы 2, пункт 1.
2. Прочитайте по учебнику §2 и §8. Изучите Рис.2, 3 и 4 на стр. 5.
3. Выпишите отдельно а) Тела: и б) Вещества: из следующего списка:
1) карандаш; 2) вода; 3) капля воды; 4) льдина; 5) лёд; 6) железо; 7) воздух;
8) кусок мела; 9) алюминий; 10) медный провод; 11) резина; 12) стекло.
Тема 3. Измерение физических величин.
1. Таблица знакомых физических величин.
При проведении опытов и наблюдений приходится производить измерения физических величин. Для каждой физической величины требуется выбрать единицу измерения. Чтобы с помощью выбранной единицы измерить величину, требуется измерительный прибор. Физическую величину обозначают буквой.
Физическая
величина
Единица измерения в системе СИ
Буква и
пример
Прибор для
измерения
1.
Длина, путь
метр
s = 5 м
линейка, счётчик
2.
Время
секунда
t = 5 с
часы, секундомер
3.
Масса
килограмм
m = 5 кг
весы
4.
Температура
градус Цельсия
t = 5С
термометр, градусник
5.
Скорость
метр в секунду
v = 5 м/с
спидометр
2. Приставки увеличения и уменьшения.
Мега
кило
1
деци
санти
милли
микро
миллион
тысяча
1
десятая
сотая
тысячная
миллионная
1 Мм
1 км
1 м
1 дм
1 см
1 мм
1 мкм
1 000 000 м
1 000 м
1 м
0,1 м
0,01 м
0,001 м
0,000 001 м
6 цифр
3 цифры
1 цифру
2 цифры
3 цифры
6 цифр
Примеры: 1) чтобы Мегаметры превратить в метры, надо запятую перенести вправо на 6 цифр: 0,5 Мм = 500 000 м; 2) чтобы метры превратить в километры, надо запятую перенести влево на 3 цифры: 200 м = 0,2 км.
Задание на уроке.
1. Выполните преобразование единиц измерения на оценку "3" (все уметь!):
1) 5 км = … м; 2) 150 км = … м; 3) 1,2 км = … м; 4) 0,12 км = … м;
5) 6 000 м = … км; 6) 120 000 м = … км; 7) 2 500 м = км; 8) 360 м = … км;
9) 60 дм = … м; 10) 500 дм = … м; 11) 2,3 м = … дм; 12) 0,45 м = дм;
13) 500 см = … м; 14) 150 см = … м; 15) 20 см = …м; 16) 5 см = … м.
2. Выполни преобразование единиц измерения длины на "4" и "5":
1) 0,062 Мм = … м; 2) 12,5 км = … м; 3) 750 000 м = … Мм; 4) 51 м = … км;
5) 840 дм = … м; 6) 0, 35 м = … дм; 7) 900 см = … м; 8) 2,1 м = … см;
9) 0,87 м = … мм; 10) 44 мм = … м; 11) 6 м = … мкм; 12) 1 000 мкм = … м.
Дома: 3. Прочитайте §6 "Физика и техника". Умейте ответить на подобные вопросы: Кто объяснил теорию света? Когда Ю.А.Гагарин облетел Землю? Чем знамениты Нейл Армстронг и Эдвин Олдрин?
4. Уметь заполнять Таблицу знакомых физических величин из пункта 1.
Физическая
величина
Единица измерения в системе СИ
Буква и
пример
Прибор для
измерения
1.
а) … …
метр
б) … = …
в) … , …
2.
г) …
д) …
t = 5 с
е) …, …
5. Превратите единицы длины (на оценку "3"):
1) 20 км = … м; 2) 1 500 м = … км; 3) 500 м = … км; 4) 0,2 км = … м; 5) 20 м = … км;
6) 125 дм = … м; 7) 1,5 м = … дм; 8) 250 см = … м; 9) 25 см = … м; 6) 1,3 м = … см.
6. Выполни преобразование единиц измерения длины на "4" и "5":
1) 0,65 Мм = … м; 2) 200 км = … м; 3) 25 м = … км; 4) 4 000 дм = … м;
5) 0,95 м = … дм; 6) 30 м = … см; 7) 0,5 см = … м; 8) 2 500 мм = … м.
Тема 4. Цена деления и показание прибора. §4 и §5
1. Цена деления и показание прибора.
Как узнать, сколько миллилитров воды налито в мензурку?
1) Сперва найдем цену деления мензурки. Уровень воды находится между числами 40 мл и 20 мл, и между этими числами всего 5 делений.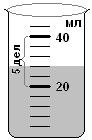
Чтобы найти цену одного деления, надо из бóльшего числа 40 мл вычесть меньшее 20 мл и разделить на число делений:
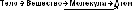 - это цена деления.
- это цена деления.
2) Вода в мензурке налита выше 20 мл на 2 деления. Чтобы найти показание прибора (сколько воды налито), надо к меньшему числу 20 мл прибавить цену деления 4 мл, умноженную на 2 дел:
20 мл + 4 мл·2 = 20 мл + 8 мл = 28 мл - это показание прибора.
2. Погрешность измерения прибора. Предел измерения прибора.
На рисунке цена одного деления мензурки равна 4 мл, а воды налито в мензурку 28 мл. Но на самом деле воды могло быть чуть меньше или чуть больше. Точные измерения невозможны! Всегда будет ошибка измерения.
Погрешность измерения в физике принято брать за половину цены деления: 4 мл : 2 = 2 мл. Тогда показание прибора с учётом погрешности измерения будет: V = 28 мл 2 мл. Значит, объём воды в мензурке приблизительно от 26 мл до 30 мл.
Предел измерения прибора ограничивается наибольшим числом на шкале. Данной мензуркой можно измерить наибольший объём воды до 40 мл.
Задание на уроке.
1. В учебнике на стр.160 в Лабораторной работе №1 по рис.177 найдите:
а) цену деления мензурки; б) показание прибора (объём налитой воды);
в) погрешность измерения и запишите объём воды; г) предел измерения.
Решение. а) Цена деления: (40 мл - 30 мл) : 2 = 5 мл; б) 30 мл + 5 мл∙1 = 35 мл;
в) погрешность 5 мл:2 = 2,5 мл; V = 35 мл ± 2,5 мл; г) предел измерен. 50 мл.
2. По такому же плану решите на стр.8-9 рис.7 (мензурка), рис.10 (секундомер) и рис.11-12 (термометры).
3. Подготовка к Лабораторной работе №1 (на следующем уроке!). У каждого на столе будет мензурка с водой. Выполните все 4 действия а), б), в) и г).
Дома: 4. На оценку "3" выучите решение задачи из данной Темы 4 и решите по рисунку аналогичную задачу самостоятельно:
а) цена деления; б) показание прибора;
в) погрешность измерения и объём воды в мензурке;
г) предел измерения данной мензурки.
5. На рисунке дан термометр с единицей измерения ºС (градус). Запишите показание термометра с погрешностью в половину цены деления:![]()
6. На рисунке пружина динамометра растянута: динамометр измеряет силу в ньютонах (F = 15 Н). . Выполните все 4 действия: а), б), в) и г).
![]()
Тема 5. Молекулярная теория строения вещества. §7
1. Первое положение молекулярного строения вещества.
Прочитайте снова в Теме 2 пункт 2.Вещество состоит из молекул и атомов и пункт 3.Молекулы очень маленькие. К написанному о молекулах нужно добавить ещё два очень важных свойства.
а) Молекулы одного и того же вещества одинаковы, в каком бы состоянии вещество ни находилось. Например, вода может быть твёрдой (лёд), жидкой и газообразной (водяной пар). Но во всех случая молекулы воды имеют одинаковые размеры и одинаковый состав: Н2О.
б) Между молекулами есть промежутки. Обычно при нагревании промежутки между молекулами увеличиваются, а при охлаждении - расширяются. Поэтому при нагревании тела расширяются, а при охлаждении сжимаются.
Умейте отвечать на вопрос: Почему при нагревании тела расширяются? Потому, что при нагревании увеличиваются ПРОМЕЖУТКИ между молекулами, а не сами молекулы!
Задание на уроке.
1. Рассмотрите в учебнике на стр.16 рис. 16 и 17. Объясните, почему после нагревания стальной шарик не проходит сквозь кольцо (читайте абзац "Проделаем опыт").
2. Рассмотрите на стр.17 рис.18 и объясните опыт (прочитайте всю стр.17).
А теперь сформулируем Первое положение молекулярной теории.
1. Все вещества не сплошные, а состоят из молекул, а молекулы состоят из атомов. Молекулы очень маленькие и не видны даже в микроскоп. Между молекулами есть промежутки. Молекулы одного и того же вещества всегда одинаковые.
2. Подготовка к Лабор. работе №2. Измерение размеров малых тел.
Длину провода легко измерить с помощью обычной миллиметровой линейки, а вот диаметр (толщину) измерить труднее - ответ получится слишком приближённым. Поэтому провод наматывают на круглый стержень, чтобы витки плотно прилегали (например, 10 витков). Длину 10 витков измерить уже легко, допустим получилось 12 мм. Значит, диаметр d = 12 мм:10 = 1,2 мм.
Точно также трудно измерить диаметр одной горошины. Но если в полоску пластилина укрепить 8 горошин плотно друг к другу, до длину ряда измерить легко, например, 2,4 см. Тогда диаметр горошины: d = 2,4 см:8 = 0,3 см = 3 мм.
Дома: 3. По рисунку вычислите а) диаметр провода; б) диаметр дробинки.

4. Выучите Первое положение молекулярной теории! Если в опыте с шариком и кольцом нагреть только кольцо, пройдёт ли шар сквозь кольцо?
Тема 6. Движение молекул. Диффузия. Броуновское движение. § 9
1. Второе положение молекулярного строения вещества.
2. Молекулы всех веществ движутся. Движение молекул непрерывно, никогда не прекращается. Молекулы движутся беспорядочно (хаотически). Чем молекулы движутся быстрее, тем больше температура тела.
Перед нами два одинаковых медных шарика из одинаковых атомов меди, но один шарик холодный, а другой горячий. Чем отличаются горячий шарик от холодного? Оказывается, в горячем шарике атомы ДВИЖУТСЯ быстрее, чем в холодном! Чем больше скорость молекул, тем выше температура.
Движение молекул доказывают два очень важных явления: диффузия и броуновское движение.
2. Диффузия. §9
Опр. Диффузией наз. явление взаимного проникновения молекул одного вещества между молекулами другого вещества.
Опыт 1. Диффузия в газах. Если в одном конце комнаты открыть флакон с духами, то через несколько секунд запах духов слышен в другом конце комнаты. Молекулы духов проникают между молекулами воздуха - происходит диффузия. Опыт показывает, что диффузия в газах происходит быстро: секунды или минуты.
Опыт 2. Диффузия в жидкости. Две жидкости - чистая вода и голубой раствор медного купороса постепенно перемешиваются друг с другом благодаря движению молекул. Этот опыт описан на стр. 21, рис. 23. Диффузия в жидкости происходит медленно: несколько часов и даже дней.
Опыт 3. Диффузия в твёрдых телах. Гладкие пластины из свинца (серый) и золота (жёлтый) прижимают друг к другу. Через 4-5 лет атомы золота и свинца проникают друг между другом на глубину 1 мм, и их невозможно оторвать (стр.22, рис.25). Диффузия в твёрдых телах идёт очень медленно: месяцы, годы. Но не во всех твёрдых телах идёт диффузия. Например, два камня могут сколь угодно долго соприкасаться, но не "прорастут" друг в друга. Это зависит от прочности кристаллической решётки твёрдого вещества.
Как скорость диффузии зависит от температуры? Чем больше температура, тем диффузия идёт быстрее, так как молекулы движутся быстрее.
3. Явление броуновского движения.
Явление броуновского движения доказывает, что молекулы движутся непрерывно и беспорядочно. Это явление описано на стр.172-173, §1.
Английский ботаник Броун обнаружил кусочек окаменевшей смолы, в которой была капелька воды. Под микроскопом он увидел в капле воды движущиеся споры (пыльцу) растений. Он решил подождать, пока споры остановятся. Но этого так и не произошло. Под беспорядочными ударами молекул воды споры тоже двигались беспорядочно, хотя и очень медленно. Причём это движение никогда не прекращалось.
Броуновским движением наз. движение очень мелких твёрдых частиц, плавающих в жидкости.
Размеры броуновских частиц должны быть микроскопическими, иначе молекулы воды не смогут их привести в движение.
4. Что такое качественные задачи и как их решают.
В качественных задачах обычно не нужно делать математических действий, а надо дать ответ на вопрос и обосновать правильность своего ответа.
Пример. В горячем или холодном чае сахар растворится быстрее?
Решение. В горячем, т.к. чем выше температура, тем быстрее идёт диффузия.
Внимание! Если в обосновании ответа вы не опираетесь на законы физики, то задача считается нерешённой. Например, такое решение: "В горячем, потому что при большой температуре сахар растворится быстрее" не годится, т.к. вы даже не упомянули слово"диффузия" - задача не решена!
Задание на уроке. Решите качественные задачи.
а) Почему воздушные шарики с гелием через некоторое время "сдуваются"?
б) Почему в дорогих альбомах или в старинных книгах между листами с картинками кладут ещё листы белой бумаги?
в) Две одинаковые банки с огурцами в рассоле: одна банка на столе, другая в холодильнике. Одинаково ли быстро просолятся огурцы? Почему?
Дома: 1. На оценку "3" выучите наизусть рамочки. На оценку "4" прочитайте §9, а на оценку "5" прочитайте §1 в конце учебника на стр.172-173.
2. В каких веществах диффузия протекает быстро, а в каких медленно?
3. Запишите в тетради решения двух качественных задач:
а) Почему бумажной салфеткой легко вытереть мокрые руки?
б) Если потереть ладонью чистый лист бумаги, то потом на ней плохо пишет шариковая ручка. Почему?
Тема 7. Взаимодействие молекул. § 10
1. Третье положение молекулярного строения вещества.
3. Между молекулами существует взаимное притяжение и одновременно взаимное отталкивание.
Между молекулами есть промежутки, и молекулы непрерывно движутся. Почему же молекулы тела не разлетаются во все стороны? Оказывается, между молекулами есть силы притяжения. Все соседние молекулы притягивают друг друга, поэтому молекулы в жидких и твёрдых телах удерживаются вместе. А вот в газах притяжение молекул очень слабое, поэтому молекулы газа разлетаются и газ занимает весь объём сосуда.
2. Опыты на силы притяжения между молекулами.
Опыт 1. Почему трудно порвать верёвку или проволоку? Между двумя молекулами притяжение ничтожно малó. Но в сечении проволоки многие миллионы молекул, и притяжение между ними складывается и становится достаточно велико, поэтому трудно порвать верёвку или проволоку.
Если тело растянуть так, что промежутки между молекулами станут меньше одной молекулы, то между молекулами появляются силы притяжения. Если промежутки станут больше молекулы, то тело порвётся.
Разберитесь по рисунку, когда действуют силы притяжения.

Опыт 2. Почему сломанные пополам куски стекла нельзя соединить обратно?
Поверхности сломанных кусков стекла очень неровные. Если их даже плотно прижать, то всё равно не удаётся молекулы приблизить на такое расстояние, чтобы они начали притягиваться (промежутки между осколками больше молекулы).
Опыт 3. Сильно нагреем куски стекла - они станут мягкими. Если теперь их плотно прижать, то они слипнутся, потому что теперь молекулы приблизились на расстояние, меньше размера молекулы.
3. Силы отталкивания между молекулами.
Если тело сжать так, что молекулы перекрываются, то между молекулами побеждают силы отталкивания.
Опыт 4. Сожмём кусок резины и отпустим. Почему резина разжимается обратно?
Потому что молекулы перекрываются и между ними силы отталкивания станут больше, чем силы притяжения.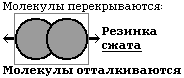
Задание на уроке. 1. Ответьте на вопросы. а) Между молекулами мела есть промежутки и молекулы движутся. Почему же молекулы не разлетаются?
б) Открытый сосуд с газом долго стоит на столе. Что произойдёт? Почему?
в) Человеческий волос выдерживает груз до 1 кг. Почему же он не рвётся?
г) Если мел сломать пополам, а куски снова приложить друг к другу, то они не удержатся вместе. Почему?
д) А если два куска пластилина прижать, то они слипнутся. Почему?
Если резину сжать и отпустить, то она разжимается - такое свойство резины называется упругостью. Объясните упругость резины.
Дома: 1. Выучите 3-тье положение молекулярной теории.
2. Объясните, при каких расстояниях между молекулами резины:
а) молекулы притягиваются; б) молекулы отталкиваются; в) резина рвётся.
Тема 7 (Продолжение). Явление смачивания. Повторение. §10
1. Явление смачивания (несмачивания).
Вода смачивает одни твёрдые тела (стекло, металлы, древесину, бумагу) и не смачивает другие (воск, парафин, кусок жира). Так и любая жидкость: одни тела смачивает, а другие не смачивает.
 Например, паста в авторучке смачивает бумагу, и благодаря этому мы можем писать, а на стекле писать пастой невозможно. Явление смачивания объясняется притяжением молекул жидкости и твёрдого тела (см. опыт на стр.25, рис.27).
Например, паста в авторучке смачивает бумагу, и благодаря этому мы можем писать, а на стекле писать пастой невозможно. Явление смачивания объясняется притяжением молекул жидкости и твёрдого тела (см. опыт на стр.25, рис.27).
Если жидкость смачивает стенки сосуда, то жидкость приподнимается вдоль стенок, потому что молекулы сосуда сильнее притягивают молекулы жидкости, чем молекулы жидкости притягивают друг друга.
Если жидкость не смачивает стенки сосуда, то жидкость опускается вдоль стенок, потому что молекулы сосуда слабее притягивают молекулы жидкости, чем молекулы жидкости притягивают друг друга. Например, вода не смачивает капустный лист, поэтому капли воды скатывается с него в виде шариков.
Задание на уроке. 1. Ответьте на вопросы. а) По жирной посуде вода скатывается шариками. Смачивает или не смачивает вода жирную поверхность?
б) Зачем водоплавающие птицы смазывают перья жиром?
в) На столе два стакана с водой: чистый и жирный. Как их различить на глаз?
г) Какие молекулы притягиваются сильнее: молекулы воды друг с другом или молекулы воды с молекулами стекла? Смачивается ли стекло водой?
д) Молекулы воды притягиваются между собой сильнее, чем молекулы воды и парафина. Смачивается ли парафин водой?
2. Прочитайте опыт на стр.24-25 по рис.27 (абзац "К пружине подвешивают…")
3. Решите две задачи из Упражнения 2 на стр. 26.
2. Повторение. Три положения молекулярного строения вещества.
Прочитайте все три положения 1, 2 и 3 (Темы 5,6 и 7). Выделим в них главное.
1. Все вещества состоят из молекул (или атомов) и между ними есть промежутки. При нагревании тела расширяются, при охлаждении - сжимаются..
2. Молекулы непрерывно (не прекращаясь) и беспорядочно движутся. Чем горячее тело, тем быстрее движутся молекулы.
3. Молекулы могут взаимно притягиваться или отталкиваться: при растяжении тела молекулы притягиваются, а при сжатии тела молекулы отталкиваются.
В теме "Строение вещества" были изучены три физических явления:
а) диффузия, б) броуновское движение, в) смачивание-несмачивание.
Прочитайте определения этих трёх явлений.
Дома: 1. На оценку "3" выучите все три положения молекулярной теории.
2. Повторите Задания на уроке двух последних уроков.
Тема 8. Три агрегатных состояния вещества. §11, 12.
Почти все вещества могут быть в трёх агрегатных состояниях. Возьмём вещество вода: в твёрдом состоянии - это лёд, в жидком состоянии - это вода и в газообразном состоянии - это водяной пар. Но при этом молекулы воды остаются всё время одинаковыми: Н2О.
Чтобы вещество из твёрдого состояния превратить сначала в жидкое, а затем в газообразное, его надо нагревать. На морозе ниже 0С вода в виде льда, от 0С до 100С - жидкая вода, а при температуре выше 100С вода переходит в газообразное состояние - водяной пар. Например, железо тоже бывает в трёх агрегатных состояниях, но чтобы железо стало жидким, а потом газообразным, его надо очень сильно нагреть: сначала железо плавится, потом кипит!
Чтобы вещество превратить из газообразного состояния в жидкое, а потом в твёрдое, его надо охладить. Например, воздух при очень сильном охлаждении можно превратить в жидкость, а затем в твёрдое состояние, как лёд.
Агрегатные
состояния:
Твёрдое
Жидкое
Газообразное
Как расположены
молекулы? Как они
притягиваются?
Молекулы расположены вплотную, сильно притягиваются (кристаллы).
Молекулы расположены вплотную, но слабо притягиваются.
Молекулы расположены далеко друг от друга, не притягиваются.
Как молекулы
движутся?
Колеблются на месте, в некоторых вещ-вах редко совершают перескоки.
Быстрее колеблются на месте, часто совершают перескоки.
Быстро летают по всему объёму, соударяются друг с другом.
Сохраняют ли тела
объём и форму?
Тела сохраняют объём и форму.
Объём сохраняют, но принимают форму сосуда.
Занимают весь объём, принимают форму сосуда
Скорость диффузии.
Диффузия не идёт или идёт очень медленно (месяцы, годы).
Диффузия идёт медленно (часы, дни).
Диффузия идёт очень быстро (минуты, секунды).
Тема 9. Механическое движение. §13, 14
1. Что такое механическое движение?
Чтобы узнать, движется тело или покоится, надо обязательно посмотреть на окружающие тела. Если данное тело с течением времени изменяет своё положение относительно других тел, то оно движется, а если не меняет - то покоится.
Опр. Механическим движением наз. изменение положения тела относительно других тел с течением времени.
Одно и то же тело может относительно одних тел двигаться и в то же время относительно других тел покоиться. Например, шофёр едет за рулём машины. Относительно дороги шофёр движется вместе с машиной, а относительно кабины шофёр покоится. Поэтому, чтобы ответить на вопрос: "Движется тело или покоится?", надо сначала спросить: "Относительно чего?".
2. Что такое траектория и путь?
Учитель провёл мелом на доске линию. Эту линию в физике называют траекторией движения мела. Но траектория не всегда видимая линия. Например, птица летит по невидимой траектории, а траектория реактивного самолёта долго видна на небе (см. рис.33-35, стр.31).
Если измерить длину траектории (в сантиметрах, метрах или километрах), то получим физическую величину, которую называют путь s.
Опр. Траекторией наз. линия, по которой движется тело. Путь - это длина траектории.
Пройденный телом путь в физике обозначают буквой s и в системе СИ путь измеряют только в метрах, например, s = 5 м.
Если путь измерен в километрах, дециметрах или других единицах, то при решении задач их надо превратить в метры - система СИ.
кило
1
деци
санти
милли
1 км
1 м
1 дм
1 см
1 мм
1 000 м
1 м
0,1 м
0,01 м
0,001 м
По таблице видно, как надо переносить запятую, чтобы получить путь в метрах:
1) 2 км = 2 000 м; 2) 12,5 км = 12 500 м; 3) 0,48 км = 480 м; 4) 34 дм = 3,4 м;
5) 0,6 дм = 0,06 м; 6) 200 см = 2 м.
3. Какое движение называют равномерным?
Пусть машина трогается с места: за 1-ую секунду она прошла 1метр, за 2-ую секунду - 3 метра, за 4-ую сек.- 10 м. Машина двигалась неравномерно. Но потом машина за каждую секунду стала проходить по 10 м с постоянной скоростью. Теперь машина стала двигаться равномерно.
Опр. Неравномерным наз. движение, при котором тело за равные промежутки времени проходит различные пути.
Опр. Равномерным наз. движение, при котором тело за любые равные промежутки времени проходит равные пути.
Задание на уроке. 1. Превратите в систему СИ единицы измерения пути:
1) 12 км = … м; 2) 0,5 км = … м; 3) 1,48 км = … м; 4) 80 дм = … м;
5) 200 дм = … м; 6) 200 см = … м; 7) 6 дм = … м; 8) 5 см = … м.
2. Относительно каких тел движется водитель, едущий по дороге?
а) Относительно дерева у дороги; б) относительно фары автомобиля;
в) относительно колеса автомобиля; г) относительно Солнца.
3. Равномерно или неравномерно движется тело: а) шар по наклонной плоскости за первую секунду 10 см, за вторую секунду 20 см, за третью - 30 см;
б) птица за первую минуту 300 м, за две минуты 600 м, за три минуты 900 м?
Дома: 4. Выучите определения в рамочках.
5. Превратить в систему СИ (на оценку "3" обязательно уметь решать всё!):
1) 3 км = … м; 2) 24,5 км = … м; 3) 0,84 км = … м; 4) 120 дм = … м;
5) 45 дм = … м; 6) 500 см = … м; 7) 10 дм = … м; 8) 9 см = … м.
Тема 10. Скорость. §15
 1. Что такое скорость движения?
1. Что такое скорость движения?
Для измерения быстроты движения в физике есть физическая величина скорость. Запомни пример вычисления скорости.
Путь от Гауфа до Звонарёв-Кута 15 км пешеход проходит за 3 часа. За каждый час он проходит по 5 км. Значит, скорость пешехода 5 км в час. Чтобы найти скорость, надо путь делить на время.
Опр. Скоростью тела при равномерном движении наз. отношение пути ко времени, за которое этот путь пройден.
Эта формула скорости верна для равномерного движения. В системе СИ скорость измеряется в метрах в секунду.![]()
2. Как превращают единицы скорости в систему СИ?
 С такой скоростью бежит сильный спортсмен стометровку!
С такой скоростью бежит сильный спортсмен стометровку!
Запомни! 18 км/ч = 5 м/с; 36 км/ч = 10 м/с; 54 км/ч =15 м/с; 72 км/ч = 20 м/с.
3. Физические величины бывают векторные и скалярные.
Например, одна машина движется со скоростью 60 км/ч в Омск, а оттуда навстречу - другая машина с такой же скоростью. Числовые значения скорости у обеих машин одинаковы (60 км/ч), но направления разные. Значит, скорость кроме числового значения имеет ещё и направление.
Опр. Векторными наз. физические величины, которые кроме числового значения имеют ещё и направление. Скорость - векторная величина.
Опр. Скалярными наз. физические величины, которые имеют только числовое значение (направления нет). Это масса, длина, время, температура.
4. Превратите единицы скорости в систему СИ.
Задание на уроке. 1. Превратите в систему СИ единицы измерения скорости.
Устно: а) 18 км/ч = … ; б) 36 км/ч = … ; в) 72 км/ч = … ; г) 144 км/ч = … .
Письменно: д) 54 км/ч = … = … ; е) 108 км/ч = … = … .
2. Превратите единицы скорости в систему СИ и сверьте с Таблицей 1, стр.37:
а) Улитка ползёт со скоростью 1,4 мм/с. б) Скворец со скоростью 1,2 км/мин.
в) Самолёт летит со скоростью 900 км/ч. г) Пуля летит со скоростью 42,9 км/мин.
д) Черепаха ползёт со скор. 4,8 м/мин. е) Земля летит вокруг Солнца 30 км/с.
Решай эти задачи по образцу:
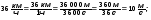
5. Решение задач на вычисление скорости.
Образец оформления задачи.
Конькобежец пробежал 1 500 м за 120 секунд. Найти скорость в системе СИ.
Дано:
Решение.
s = 1 500 м
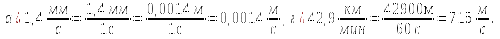
t = 120 c
v - ?
Ответ. v = 12,5 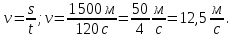 .
.
Задание на уроке. 3. Вычислите скорость тела по формуле скорости (в системе СИ) и сверьте с таблицей в учебнике:
а) За 4 с муха пролетела 20 м. б) Конькобежец пробежал 400 м за 30 с.
в) Скворец пролетел 144 км за 2 часа. г) Автомобиль "Жигули" 432 км за 2 часа.
Дома: 4. Выучите определение скорости, формулу скорости (какой буквой обозначается величина и в каких единицах в СИ измеряется). Запишите так:
s [м] - путь; t [с] - время; v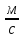 - скорость.
- скорость.
5. Вычислите скорость тела по формуле скорости (в системе СИ) и сверьте с таблицей в учебнике: а) муха за 30 с может пролететь 150 м;
б) пуля автомата Калашникова за 2 с пролетит 1 430 м.
6. Письменно превратите в систему СИ единицы скорости:
а) 9 км/ч; б) 54 км/ч; в) 45 км/ч; г) 120 м/мин; д) 0,5 км/с; е) 7,2 км/мин.
7. Решите качественные задачи (можно устно):
1) Движется ли наша школа? Как надо отвечать на этот вопрос?
2) В вагоне поезда на столике лежит книга. В покое или движении находится книга относительно а) стола; б) рельсов; в) человека, идущего по вагону?
3) Рядом летят два журавля. Какова их скорость относительно друг друга?
Тема 11. Задачи на расчёт пути и времени. §16
1. Решение задач на вычисление пути, времени, средней скорости.
Чтобы научиться вычислять путь s или время t по формуле скорости 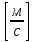 можно обращаться к задаче про Гауф и Звонарёв-Кут (см. Тема 11, п.1).
можно обращаться к задаче про Гауф и Звонарёв-Кут (см. Тема 11, п.1).
1) Чтобы найти путь s = 15 км, надо скорость v = 5 км/ч умножить на время t = 3 ч.
2) Чтобы найти время t = 3 ч, надо путь s = 15 км разделить на скорость v = 5 км/ч.
Формула пути: 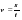 ; формула времени:
; формула времени: 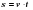 .
.
Запомни! 1) Если единицы измерения в системе СИ (метры и секунды), то их не трогаем. А если единица измерения не в СИ (км, дм, мин, часы), то их превращаем в систему СИ и записываем рядом.
1. Задача на нахождение скорости.
Конькобежец пробежал 1 500 м за 2 минуты. Найти скорость в системе СИ.
Дано:
СИ
Решение.
s = 1 500 м
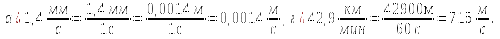
t = 2 мин
120 с
v - ?
Ответ. v = 12,5 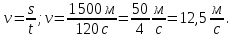 .
.
Здесь путь 1 500 м был дан в системе СИ - его оставляем, а время 2 мин = 120с.
2. Задача на нахождение пути.
Какой путь пройдёт автомобиль со скоростью 54 км/ч за 5 мин?
Дано:
СИ
Решение.
v = 54 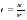
15 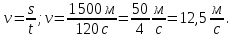
54 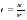 =
= 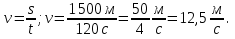 .
.
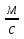
t = 5 мин
300 с
s - ?
Ответ. s = 4,5 км.
В этой задаче пришлось обе данные величины превратить в систему СИ. Если скорость можете превратить устно, то это действие записывать не надо. Если путь в ответе составляет сотни метров, то ответ оставляют в метрах. Если путь составляет тысячи метров, то ответ выражают в километрах.
3. Задача на нахождение времени.
За сколько времени спутник облетит вокруг Земли расстояние 48 000 км со скоростью 8 км/с? Эту задачу проще решить, не превращая в систему СИ.
Дано:
Решение.
v = 8 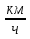
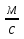
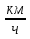
s = 48 000 км
t - ?
Ответ. t = 1 ч 40 мин.
Внимание! Решение любой из трёх задач начинается с формулы для запоминания 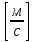 , из которой потом выражают путь
, из которой потом выражают путь 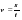 или время
или время 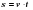 .
.
4. Задача на нахождение средней скорости.
Турист шёл 3 часа со скоростью 6 км/ч, потом ехал на велосипеде 2 часа со скоростью 18 км/ч. Найти среднюю скорость туриста: надо весь путь s = s1 + s2 поделить на всё время t = t1 + t2. Сюда включают также время стоянок!
Дано: Решение.
t1 = 3 ч
v1 = 6 км/ч
t2 = 2 ч
v2 = 18 км/ч Ответ. vср = 10,8 км/ч.
vср - ?
Задание на уроке. 1. За 5 мин птица пролетела 3 км. Найти скорость птицы.
2. Какой путь пройдёт поезд за 2,5 часа со скоростью 72 км/ч?
3. За сколько времени тело пройдет 1,2 км при скорости 20 м/с?
4. Шар катился 4 с со скоростью 2,5 м/с, затем 16 с со скоростью 0,5 м/с. Найти среднюю скорость шара.
Дома: 5. Стриж пролетел 1,2 км за 1 минуту. Найти скорость стрижа.
6. Какой путь пройдёт автомобиль со скоростью 72 км/ч за 50 с?
7. За сколько времени пройдёт поезд участок пути 20 км со скоростью 40 км/ч?
8. Турист шёл 3 ч со скоростью 6 км/ч, потом 1 час отдохнул и ещё шёл 2 ч со скоростью 3 км/ч. Найти среднюю скорость туриста за всё время движения.
Тема 12. Первый закон Ньютона. Инерция. §17
1. Первый закон Ньютона: движение тела по инерции.
Рассмотрим опыт с тележкой, катящейся с горки (рис.41, стр.41). На рисунке
а) сопротивление кучи песка велико, поэтому тележка быстро останавливается. б) Если песок разгладить, трение будет меньше и тележка прокатится дальше. в) Если песок совсем убрать, то тележка прокатится ещё дальше.
Отсюда получаем вывод: если бы трения совсем не было, то тележка катилась бы сколь угодно долго. Впервые этот закон физики открыл Галилео Галилей. Раньше Аристотель думал по-другому, что любое движущееся тело всегда, в конце концов, остановится. Но оказалось, что если в космосе бросить камень, где не мешает трение, то он будет лететь сколь угодно долго.
Английский учёный Исаак Ньютон назвал этот закон Галилея первым законом механики. Ньютон открыл ещё два закона механики.
1-ый закон Ньютона. Если на данное тело не действуют другие тела, то данное тело либо покоится, либо движется прямолинейно и равномерно.
Первый закон механики ещё называют законом инерции.
Инерцией наз. явление сохранения скорости тела, если на него не действуют другие тела. Тело движется по инерции, если выполняется 1 закон Ньютона.
Тело может либо покоится по инерции, либо двигаться по инерции. Приведём пример движения по инерции. Велосипедист разогнался и отпустил педали: обычно говорят, что дальше велосипедист продолжает двигаться по инерции. Хотя на самом деле из-за трения скорость велосипеда понемногу уменьшается, и скорость не вполне сохраняется, но всё равно считают такое движение по инерции. Опасно переходить дорогу перед близко идущим транспортом, т.к. автомобиль нельзя мгновенно остановить из-за явления инерции.
2. Качественные задачи на инерцию.
Молоток на ручку можно насадить двумя способами.
Задача 1. Почему молоток насаживается на ручку, если резко ударить ручкой об опору (рис.1)?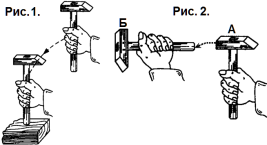
Решение. Потому что на опоре ручка остановилась, а молоток продолжает двигаться по инерции.
Задача 2. Почему молоток насаживается на ручку, если ударить молотком А по ручке молотка Б (рис.2)?
Решение. Потому что от удара ручка пришла в движение, а молоток Б продолжает покоится по инерции.
Аналогично решаются две качественные задачи про пассажиров автобуса.
Задача 3. В какую сторону и почему отклоняется стоящий пассажир, когда автобус резко тормозит?
Решение. При торможении ноги пассажира вместе с полом автобуса останавливаются, а туловище движется по инерции туда, куда двигался автобус.
Задача 4. В какую сторону и почему отклоняется стоящий пассажир, когда автобус трогается с места?
Решение. При трогании с места ноги пассажира начинают двигаться в направлении движения автобуса, а туловище покоится по инерции относительно земли, но относительно автобуса туловище движется в обратную сторону.
Задание на уроке. Рассмотрим ещё качественные задачи на явление инерции.
5. Что будет со всадником, если лошадь внезапно остановится?
6. Аналогично задаче про пассажиров решите две задачи на чистку ковров:
а) Почему удаляется пыль при встряхивании ковра?
б) Почему удаляется пыль при выколачивании ковра хлопушкой?
Дома: 1. Выучите обе рамочки: 1-ый закон Ньютона и определение инерции.
2. На оценку "3" уметь записать решение первых трёх качественных задач.
Тема 13. Второй и третий законы Ньютона. §17 и 18
1. Второй закон Ньютона: от чего меняется скорость тела?
Опыт 1. Чтобы тело начало двигаться, на него должно подействовать другое тело. Например, футбольный мяч начнёт двигаться, если его ударить ногой.
Опыт 2. Чтобы движущееся тело остановилось, на него должно подействовать другое тело. Катящийся по траве футбольный мяч останавливается под действием трения о траву. Или нога футболиста может остановить мяч.
Опыт 3. Чтобы изменить направление вектора скорости, опять на тело должно подействовать другое тело. Теннисный мяч меняет направление движения при ударе о ракетку.
2-ой закон Ньютона. Чтобы тело изменило величину или направление скорости, на него должно подействовать другое тело.
Запомни! Что значит: физическая величина изменилась? Это значит, что она уменьшилась или увеличилась, а вектор может изменить направление.
Задание на уроке. 1. Прочитайте по учебнику §17 стр.40 (от начала до жирного шрифта). Жирным шрифтом написан тоже 2-ой закон Ньютона.
2. Выясните разницу между 1-ым и 2-ым законами Ньютона. Когда скорость тела не меняется? Когда скорость тела меняется?
2. Третий закон Ньютона: взаимодействие тел.
Действие одного тела на другое тело может быть сильным или слабым. Для измерения действия одного тела на другое вводится физическая величина, которая называется сила. Сила в физике обозначается буквой F и измеряется в ньютонах. Например, F = 5 Н. Сила имеет направление и поэтому является векторной величиной, как и скорость.
Опр. Силой наз. действие другого тела на данное тело. Сила - векторная физическая величина (имеет направление и измеряется в ньютонах).
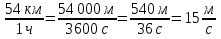 Если одно тело действует на другое, то и другое тело действует на первое, то есть тела действуют друг на друга. Говорят, что тела взаимодействуют.
Если одно тело действует на другое, то и другое тело действует на первое, то есть тела действуют друг на друга. Говорят, что тела взаимодействуют.
При взаимодействии тел всегда выполняется 3-ий закон Ньютона: одно тело действует на другое тело с такой же силой, как другое тело действует на первое. Например, нога футболиста действует на мяч с силой F1 = 50 Н, тогда и мяч действует на ногу с силой F2 = 50 Н. Но векторы этих сил направлены в противоположные стороны.
Запомни: с какой силой большое тело ударит по маленькому телу, с такой же силой маленькое тело ударит по большому телу!
3-ий закон Ньютона. При взаимодействии два тела действуют друг на друга с равными силами. Действие равно противодействию: F1 = F2.
3. Качественные задачи на законы Ньютона.
1. Подберите номер закона Ньютона к каждой букве. Ответ запишите в виде шестизначного числа (например, 2,1,1,3,3,2).
а) Тело движется прямолинейно и равномерно; б) тело изменяет скорость;
в) мяч отскакивает от ноги футболиста; г) магнит притягивает к себе железо;
д) вектор скорости тела изменил направление; е) тело покоится.
2. Боксёр ударил соперника в лоб с силой 200 Н. С какой силой лоб соперника мог ударить по перчатке боксёра? Выберите один верный ответ.
а) 50 Н; б) 100 Н; в) 200 Н; г) 400 Н; е) неизвестно.
3. Шар массой 2 кг ударил по шару массой 4 кг, с силой 6 Н. С какой силой второй шар ударил по первому шару?
4. За плотным забором едет велосипедист, у которого видна только шляпа. Как можно догадаться, что велосипедист усиленно крутит педали?
Дома: 1. На оценку "3" выучите все три закона Ньютона и определение силы.
2. Повторите решения качественных задач 1-4 из пункта 3.
3. Прочитайте по учебнику §18. Разберитесь с явлением отдачи при выстреле.
Тема 14. Масса тела (лабораторная работа №3). §20
1. Измерение массы тела.
Любое тело обладает массой: атом, микроб, Земля, звёзды и даже частички света. В системе СИ масса измеряется в килограммах, обозначается буквой m = 5 кг. Существует эталон килограмма, изготовленный из сплава платины и иридия, который хранится во Франции. Там же хранится эталон длины. Масса m, длина (путь) s и время t являются основными физическими величинами и в системе СИ измеряются в основных единицах: килограмм кг, метр м, секунда с.
Таблица единиц массы:
Тонна (т)
Центнер (ц)
килограмм (кг)
грамм (г)
миллиграмм (мг)
1 000 кг
100 кг
1 кг
0,001 кг
0,000 001 кг
При решении задач единицы массы обычно превращают в кг - в систему СИ.
Примеры: 1) 0,65 т = 650 кг; 2) 1,2 ц = 120 кг; 3) 250 г = 0,25 кг; 4) 50 г = 0,05 кг.
При взвешивании массы тел с использованием миллиграммовых гирек:
1) 5 г 200 мг = 5,2 г = 0,0052 кг; 2) 6 г 50 мг = 6,050 г = 0,00605 кг.
Задание на уроке. 1. Выполните преобразование единиц массы:
а) 1,5 т = … кг; б) 0,35 ц = … кг; в) 7 200 кг = … т; г) 40 кг = … ц;
д) 3 400 г = … кг; е) 150 г = … кг; ж) 20,4 г = … кг; з) 0,25 кг = … г.
2. Превратите сперва в граммы, а потом в килограммы:
а) 1 200 мг = … г = … кг; б) 5 г 200 мг = … г = … кг; в) 500 мг = … г = … кг;
г) 6 г 50 мг = … г = … кг; д) 80 г 150 мг = … г = … кг.
2. Подготовка к Лабораторной работе №3.
На лабораторных работах по физике массу тела измеряют на рычажных весах. Главная часть весов - коромысло, к концам которой прикреплены чашки. В коробочке с разновесами есть гирьки от 100 г до 10 мг.
Пример. При взвешивании тела использовались разновесы: 100 г, 20 г, 2 г, 2 г, 200 мг. Найдите общую массу разновесов и превратите в килограммы.
Решение. 100 г + 20 г + 2 г + 2 г + 0,2 г = 124,4 г = 0,1244 кг.
3. Прежде, чем взвешивать тела, решите письменно следующие задания:
а) 50 г, 10 г, 1 г, 500 мг, 50 мг; б) 5 г, 2 г, 2 г, 100 мг; в) 100 г, 1 г, 50 мг, 10 мг.
4. В учебнике на стр.162 прочитайте Правила взвешивания.
5. Под руководством учителя проведите взвешивание трёх разных тел с точностью до 0,1 г. (На следующем уроке эти тела будете взвешивать сами!)
Дома: 6. На оценку "3" превратите единицы измерения массы:
а) 2,6 т = … кг; б) 3,5 ц = … кг; в) 2 500 кг = … т; г) 400 кг = … ц;
д) 8 500 г = … кг; е) 450 г = … кг; ж) 20 г = … кг; з) 0,75 кг = … г.
7. Найдите общую массу разновесов и превратите в килограммы.
а) 100 г; 50 г; 10 г; 2 г; 100 мг; б) 50 г; 2 г; 2 г; 100 мг; 50 мг;
в) 100 г; 2 г; 50 мг; г) 5 г; 2 г; 2 г; 20 мг; 20 мг.
8. Повторите Правила взвешивания на стр.162 учебника!
Тема 15. Решение задач на взаимодействие тел. §18 и 19
1. Как зависит скорость тел от их массы.
Рассмотрим опыт. Две тележки массами m1 = 6 кг и m2 = 2 кг соединены согнутой пластиной, которая, как пружина расталкивает тележки в разные стороны.
По 3-ему закону Ньютона обе тележки через пружину взаимодействуют друг с другом с одинаковой силой. Но разгоняться эти тележки будут неодинаково! Ясно, что лёгкая тележка разгонится до большей скорости v2 = 3 м/с, а тяжёлая тележка до меньшей скорости v1 = 1 м/с.
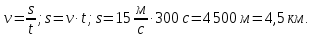 Так как масса 1-ого тела m1 = 6 кг в 3 раза больше массы 2-ого тела, то скорость первого тела v1 = 1 м/с будет в 3 раза меньше.
Так как масса 1-ого тела m1 = 6 кг в 3 раза больше массы 2-ого тела, то скорость первого тела v1 = 1 м/с будет в 3 раза меньше.
Во сколько раз масса первого тела m1больше массы второго тела m2,во столько же раз скорость первого тела v1меньше скорости второго тела v2. Скорости тел обратно пропорциональны массам тел.
Формула обратной пропорциональности: 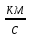 . Если три члена пропорции известны, то можно найти неизвестный четвёртый член пропорции:
. Если три члена пропорции известны, то можно найти неизвестный четвёртый член пропорции: 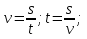 .
.
Задача на взаимодействие тел. Мальчик сидит в лодке и отталкивается от неподвижного плота со скоростью 0,6 м/с относительно воды. Масса лодки и мальчика 120 кг, а масса плота 40 кг. С какой скоростью будет двигаться плот?
Дано: Решение.
m1 = 120 кг
m2 = 40 кг
v1 = 0,6 м/с
v2 - ? Ответ. v2 = 1,8 м/с.
Задание на уроке. 1. Решите две простые задачи на взаимодействие тел.
а) Из неподвижной лодки массой 80 кг прыгает на берег мальчик массой 40 кг со скоростью 4 м/с. Найти скорость лодки.
б) При выстреле из пушки вылетает ядро массой 8 кг со скоростью 100 м/с. Найти массу пушки, если пушка при отдаче приобретает скорость 1,6 м/с.
Решим задачу а) устно, с помощью рассуждения: т.к. масса лодки 80 кг в 2 раза больше массы мальчика 40 кг, то скорость лодки v2 будет в 2 раза меньше скорости мальчика. Значит, v2 = 4 м/с : 2 = 2 м/с.
2. Папа массой 80 кг и сын 20 кг стоят на коньках и отталкиваются друг от друга. Скорость сына 3,2 м/с. Найти скорость папы. С одинаковой ли силой они отталкивают друг друга? Проверьте решение с помощью рассуждения.
Дома: 3. На оценку "3" выучите правило в рамочке и решите две задачи.
а) Из неподвижной лодки массой 60 кг прыгает на берег мальчик массой 20 кг со скоростью 3 м/с. Найти скорость лодки.
б) Папа массой 80 кг и сын 40 кг стоят на коньках и отталкиваются друг от друга. Скорость папы 2,5 м/с. Найти скорость сына.
Проверьте решения этих задач устно, с помощью рассуждения.
Дополнительные задачи на оценку "5". Если вы можете решить эти задачи, то первое задание (на оценку "3") можете дома не делать. Решите эти задачи на листочке, подпишите свою фамилию и принесите к следующему уроку.
4. Общая масса мальчика и лодки с грузом 105 кг. Мальчик выбрасывает из лодки груз массой 5 кг со скоростью 2 м/с. С какой скоростью начнёт двигаться лодка? (Подсказка: масса лодки с мальчиком стала меньше на 5 кг!).
5. Мальчик массой 40 кг бежит со скоростью 3 м/с и вскакивает на неподвижную тележку массой 60 кг. С какой скоростью будет двигаться мальчик в тележке? (Подсказка: мальчик вместе с тележкой!). Ответы: 4) 0,1 м/с; 5) 1,2 м/с.
Тема 16. Объём тела и плотность вещества. §21
1. Объём тела.
Объём тела в системе СИ измеряется в кубических метрах, обозначается V = 24 м3. Объём прямоугольного параллелепипеда находят по формуле V = a·b·h = 3 м ·2 м ·4 м = 24 м3. Так как площадь основания S = a·b, то объём можно найти также по формуле V = S·h.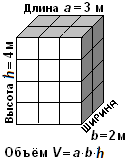
Таблица единиц объёма:
1 м3
1 дм3
1 см3
Запятую перенести на 3 знака
1 л
1 мл
0,001 м3
0,000 001 м3
1 м3 = 1 000 дм3 = 1 000 л = 1 000 000 см3
Задание на уроке. 1. Преобразуйте единицы объёма в СИ.
а) 450 дм3 = … м3; б) 20 дм3 = … м3; в) 3 000 л = … м3; г) 5 л = … м3;
д) 1 500 дм3 = … м3; е) 25 000 см3 = … м3; ж) 250 мл = … м3; з) 0,5 дм3 = … м3.
2. Преобразуйте единицы объёма друг в друга:
а) 1,2 м3 = … дм3; б) 0,08 м3 = … дм3; в) 1 200 см3 = … дм3; г) 0,5 дм3 = … см3;
д) 0,56 м3 = … л; е) 7,8 дм3 = … л; ж) 1 500 мл = … л; з) 700 мл = … см3.
2. Лабораторная работа №4. Измерение объёма тела.
Прочитайте в учебнике на стр.163 Лабораторная работа №4. С помощью мензурки можно измерить не только объём жидкости, но и объём твёрдого тела.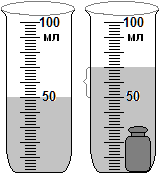
Для этого наливаем в мензурку ровно 50 мл воды. На нитке опускаем в воду тело. Уровень поднялся на 10 делений. Цена деления мензурки:
(100 мл - 50 мл):25 дел. = 2 мл.
Объём воды с телом стал: 50 мл + 2 мл∙10 = 70 мл.
Объём тела равен разности 70 мл - 50 мл = 20 мл.
Вместе с учителем измерьте объёмы нескольких тел, а на следующем уроке проделайте это самостоятельно.
3. Плотность вещества.
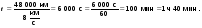 Опыт 1. Возьмём одинаковые кубики объёмом 1 см3, изготовленные из разных веществ: из сосны, из стекла и из железа. Взвешивание покажет, что эти тела имеют разные массы: 0,4 г, 2,5 г и 7,8 г, потому что у различных веществ различная плотность: у сосны плотность меньше, а у железа - больше.
Опыт 1. Возьмём одинаковые кубики объёмом 1 см3, изготовленные из разных веществ: из сосны, из стекла и из железа. Взвешивание покажет, что эти тела имеют разные массы: 0,4 г, 2,5 г и 7,8 г, потому что у различных веществ различная плотность: у сосны плотность меньше, а у железа - больше.
Опыт 2. Возьмём глыбу льда в виде параллелепипеда объёмом V = 24 м3 (см. рисунок в пункте 1). Его масса будет m = 21 600 кг. Найдём массу 1 м3 льда: для этого 21 600 кг : 24 м3 = 900 кг/м3 - это и будет плотность льда.
Чтобы найти плотность вещества, надо массу тела разделить на объём.
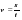
Выучите формулу: m[кг] - масса тела; V[м3] - объём тела; 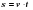 - плотность.
- плотность.
Опр. Плотностью вещества наз. физическая величина, равная отношению массы тела к его объёму.
4. Единицы плотности.
Для измерения плотности применяют три единицы измерения.
Надо твёрдо помнить: 1 м3 воды имеет массу 1 тонна = 1 000 кг;
1 литр (1 дм3) воды имеет массу 1 кг; 1 см3 воды имеет массу 1 г.
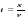
Если вещество легче воды, например, бензин, то его плотность будет:
ρбен = 710 кг/м3 = 0,71 кг/дм3 = 0,71 г/см3 (плотность меньше 1).
Если вещество тяжелее воды, например, железо, то его плотность будет:
ρжел = 7800 кг/м3 = 7,8 кг/дм3 = 7,8 г/см3 (плотность больше 1).
Плотности некоторых твёрдых, жидких и газообразных тел есть на стр. 50-51.
Задание на уроке. 3. Превратите единицы плотности в систему СИ [кг/м3]:
а) золото 19,3 г/см3; б) сосна 0,4 кг/дм3; в) мёд 1,35 кг/л;
г) бензин 0,71 кг/дм3; д) кислород 0,00143 г/мл; е) природный газ 0,0008 г/см3.
Запятая переносится вправо на 3 цифры! Проверь себя по Таблице 2 на стр.50.
Дома: 4. На оценку "3" уметь превращать дм3 и литры в систему СИ м3:
а) 15 дм3 = … м3; б) 120 дм3 = … м3; в) 30 000 л = … м3; г) 50 л = … м3.
5. Выучить опр. плотности (рамочку), формулу плотности (все 3 буквы: как называются, в чём измеряются) и запомнить плотность воды.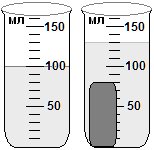
6. Единицы плотности кг/дм3, кг/л, г/см3 и г/мл превратите в СИ кг/м3:
а) 1,2 кг/дм3 ; б) 0,8 кг/л; в) 13,6 г/см3; г) 0,93 г/мл; д) 0,0013 кг/л.
7. В Лабораторной работе №4 мы измерили объём тела в 4 действия (смотрите на левой странице):
а) Начальный объём 50 мл.
б) Цена деления (100 мл - 50 мл):25 дел. = 2 мл.
в) Конечный объём 50 мл + 2 мл∙10 = 70 мл.
г) Объём тела = Конечный объём - Начальный объём =
= 70 мл - 50 мл = 20 мл.
Сделайте эти 4 действия для данного рисунка!
Тема 17. Задачи на вычисление плотности. §21 (на 2 урока)
1. Качественные задачи на плотность веществ.
Плотности веществ смотрите в учебнике в Таблицах 2-3-4 на стр.50-51.
1. Рассмотрим три качественные задачи на плотность (с решениями).
а) В стакан налили три несмешивающиеся жидкости: воду, ртуть и бензин. Сделайте рисунок и подпишите вещества.
б) Три кубика из сосны, стекла и железа имеют одинаковый объём. Какой кубик имеет наименьшую массу, а какой - наибольшую массу?
в) Три кубика одинаковой массы по 1 кг сделаны из сосны, стекла и железа. Какой кубик имеет наибольший объём, а какой - наименьший?

Решения приведены на рисунках. Плотности веществ взяты из Таблицы 3 и 2.
Задание на уроке. 2. В литровую банку помещается ровно 1 кг воды. Поместится ли в эту банку 1 кг бензина? 1кг мёда?
3. Какова масса а) 1 м3 воды б) 1 м3 машинного масла; в) 1 дм3 воды;
г) 1 дм3 серной кислоты; д) 1 см3 воды; е) 1 см3 керосина?
4. Какой объём занимает: а) 900 кг льда; б) 1 800 кг льда; в) 0,9 кг льда?
5. Какой объём имеет алюминиевый куб а) массой 2,7 кг; б) массой 2,7 г?
2. Задачи на вычисление плотности вещества.
Можно все величины сначала превратить в систему СИ, тогда и ответ получится в СИ.
1. На баночке с мёдом написано: масса 270 г, объём 200 мл. Найдите плотность мёда в системе СИ. Сверьте ответ по таблице 3 на стр. 51.
Дано:
СИ
Решение.
m = 270 г
0,27 кг

V = 200 мл
0,0002 м3
- ?
Ответ. = 1 350 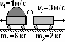 .
.
Но проще эту задачу решить, не превращая данные в систему СИ, а только ответ превратить в СИ. (Слабому ученику надёжнее решать первым способом)
Дано:
Решение.
m = 270 г
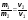
V = 200 мл
- ?
Ответ. = 1 350  .
.
2. Кирпич размерами 30см х15 см х10 см имеет массу 8,1 кг. Найти плотность.
Дано:
СИ
Решение.
а = 30 см
b = 15 см
h = 10 см
m = 8,1 кг
0,3 м
0,15 м
0,1 м
V = a∙b∙h; V = 0,3 м∙0,15 м∙0,1 м = 0,0045 м3;
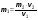
- ?
Ответ. = 1 800  .
.
3. Подготовка к Лабораторной работе №5. Измерение плотности.
Эта лабораторная работа должна быть обязательно полностью оформлена и выполнена каждым учеником. Прочитайте содержание работы на стр.164-165. Учитель показывает вам ход выполнения работы. Вычисления записывайте!
1. Разбираем коробку с разновесами и собираем весы.
2. На левую чашку кладём тело, на правую чашку - гирьки разновесов от самой большой к меньшим. Если гирька перевешивает - убираем и кладём следующую, если тело перевешивает - гирьку оставляем. Допустим, получились следующие гирьки: m = 50 г + 10 г + 2 г +2 г + 500 мг = 64 г 500 мг = 64,5 г.
3. Измеряем объём тела.
а) В мензурку налито 100 мл воды - это начальный объём.
б) Опустим в мензурку тело на нити - вода поднялась. Находим цену деления: (150 мл - 100 мл):25 делений = 2 мл - это цена одного деления.
в) Сосчитаем, на сколько делений поднялась вода: например, на 15 делений. Тогда объём тела V = 2 мл∙15 = 30 мл - это объём тела.
г) Вычислим плотность по формуле и превратим в систему СИ:

д) Перечерчиваем в тетрадь таблицу и заполняем её.
Название
вещества
Масса тела
m, г
Объём тела
V, мл
Плотность вещества
, г/мл
, кг/м3
Пластилин
64,5
30
2,15
2 150
Задание на уроке. 1. Решите задачи на вычисление плотности вещества.
а) В цистерне объёмом 50 м3 перевозят 40 тонн нефти. Найти плотность нефти и сверить по таблице 3 на стр. 51.
б) Сухой сосновый брус размерами 2 дм х 2 дм х 20 дм имеет массу 32 кг. Найти плотность сухой сосны.
2. Решите задачу, аналогичную лабораторной работе, с помощью рисунка.
а) Запишите сумму разновесов и найдите массу:
m = … + … + … + … = …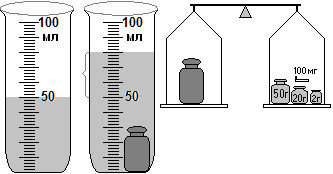
б) Найдите цену деления мензурки.
в) Сосчитайте, на сколько делений поднялась вода
и вычислите объём тела V = …∙… = … мл.
г) Вычислите по формуле плотность вещества.
В системе СИ плотность должна получиться:
2 400 кг/м3.
Дома: 3. Подготовьтесь к Лабораторной работе №5 "Измерение плотности".
4. Решите задачи на вычисление плотности вещества.
а) Найти плотность кирпича, если 2 м3 кирпича имеют массу 3,6 тонны.
б) Найти плотность сахара, если 30 см3 сахара имеют массу 48 г 300 мг.
в) Найдите плотность воздуха, если в кабинете физики длиной 10 м, шириной 6 м и высотой 3 м содержится 234 кг воздуха.
5. Решите устно качественные задачи (с помощью таблицы 2 на стр.51):
а) Какой объём занимает 7,3 кг олова? б) Какова масса 1 дм3 алюминия?
Тема 18. Найти массу и объём тела по плотности. §22
1. Вычисление массы тела m, если даны плотность и объём V.
Задачи на оценку "3" без превращения в СИ.
1. Найти массу плота из сосновых брёвен объёмом 2,5 м3.
Т. к. плотность сосновых брёвен не дана, значит, надо посмотреть в Таблицу 2 на стр.51, откуда плотность сосны 400 кг/м3.
Дано:
Решение.
V = 2,5 м3
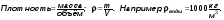 400
400  ∙2,5 М3 = 1 000 кг = 1 т.
∙2,5 М3 = 1 000 кг = 1 т.
= 400 
m - ?
Ответ. m = 1 т.
2. Какая масса мёда поместится в двухлитровую банку?
Здесь объём банки 2 л или 2 дм3, тогда плотность мёда по Таблице 2 лучше взять как 1,35 кг/дм3 (или 1,35 кг/л). Тогда в решении дм3 сокращаются!
Дано:
Решение.
V = 2 дм3
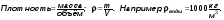 1,35
1,35 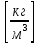 ∙2 дМ3 = 2,7 кг.
∙2 дМ3 = 2,7 кг.
= 1,35 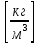
m - ?
Ответ. m = 2,7 кг.
Задачи на оценку "4" с превращением в СИ.
3. Сколько килограммов бензина поместится в 10-литровую канистру, если плотность бензина 710 кг/м3. Т.к. объём дан в литрах, а плотность дана через кубические метры м3, то надо литры тоже превратить в м3.
Дано:
СИ
Решение.
V = 10 л
0,01 м3
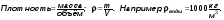 710
710  ∙0,01 дМ3 = 7,1 кг.
∙0,01 дМ3 = 7,1 кг.
= 710 
m - ?
Ответ. m = 7,1 кг.
Задание на уроке. 4. Найдите массу льдины объёмом 45 м3.
5. Оконное стекло имеет объём 400 см3. Какова его масса? (Чтобы 400 см3 не пришлось превращать в кубометры, лучше плотность взять в г/см3, а потом граммы превратить в килограммы).
6. Найдите массу воздуха в кабинете физики размерами 6мх3мх10м. Плотность воздуха возьмите округлённо 1,3 кг/м3.
2. Вычисление объёма тела V, если даны плотность и масса m.
7. Какой объём займёт 36 г водорода? Выразить в куб. метрах и литрах.
Дано:
СИ
Решение.
m = 36 г
0,036 кг
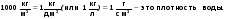
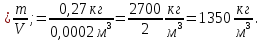
= 0,090 
V - ?
Ответ. V = 400 л.
Задание на уроке. 8. Какой ёмкости нужна канистра, чтобы налить 4 кг спирта? Выразите ёмкость канистры в литрах.
9. Найти объём алюминиевого цилиндра массой 540 г (в дм3 и в см3).
Дома: Обязательные задачи на оценку "3".
1. Найти массу поддона с кирпичом объёмом 0,5 м3.
2. Найти массу бензина в 20-литровой канистре.
3. Найти объём льдины массой 450 кг.
Задачи на "4 и 5". Если решите эти задачи, то №1,2 и 3 можно не решать.
4. Какая масса подсолнечного масла поместится в стакан 200 см3?
5. Какова масса воды в аквариуме размерами 50см х 40 см х 30 см.
6. Какой объём займёт 520 г воздуха? Плотность воздуха 1,3 кг/м3.
7. Рыболовецкий сейнер берёт в плавание 60 т нефти. Какова ёмкость бака для нефти?
Тема 19. Подготовка к контрольной работе.
1. Качественные задачи по пройденным темам.
1. Распределите термины по группам: а) тела; б) вещества; в) явления:
1) железный шарик; 2) вода; 3) диффузия; 4) машинное масло; 5) инерция;
6) оконное стекло; 7) молния; 8) кусочек мела; 9) гелий; 10) смачивание.
2. Три положения молекулярного строения вещества - вставьте слова.
Все вещества состоят из а) … . Между молекулами есть б) … .
Молекулы беспрерывно и беспорядочно в) … . Чем больше температура тела, тем молекулы г) … … . Между молекулами существует взаимное д) … и … .
3. К каждой физической величине приведите пример: температура t = 5С.
Путь а) … = 5 …; время: б) … = 5 …; скорость: в) … = 5 …; сила: г) … = 5…;
масса: д) … = 5 …; объём: е) … = 5 …; плотность: ж) … = 5 … .
4. Три агрегатных состояния 1) твёрдое; 2) жидкое; 3) газообразное. К каждому примеру с буквой а) подберите цифру агрегатного состояния. Ответ запишите в виде 8-значного числа (например, 1232 2131)
а) лёд; б) вода; в) водяной пар; г) молекулы колеблются только на месте;
д) молекулы летают по всему объёму; е) имеет постоянный объём и форму;
ж) имеет постоянный объём, но принимает форму сосуда;
з) диффузия происходит за секунды и минуты.
5. Напишите полное объяснение к качественным задачам:
а) Почему ручка не пишет, если бумага жирная?
б) Пересоленную селёдку вымачивают в воде. Какое это явление? При какой температуре это явление происходит быстрее?
в) Если резко дёрнуть санки, ребёнок может с них упасть. Почему?
6. Превратите единицы измерения в систему СИ:
а) 0,45 км = …; б) 2 мин = …; в) 36 км/час = …; г) 400 г = …;
д) 120 л = …; е) 1,2 кг/дм3 = …; ж) 0,4 г/см3 = … .
2. количественные задачи.
а) Какой путь пролетит скворец со скоростью 36 км/ч за 2 минуты?
б) Какой объём занимает 1,6 тонны керосина плотностью 800 кг/м3?
в) Какая масса углекислого газа плотностью 2 кг/м3 поместится в комнате длиной 5 м, шириной 3 м и высотой 2 м?
г) Папа массой 80 кг и сын массой 20 кг на коньках отталкиваются друг от друга. Сын откатывается со скоростью 4 м/с. Какая скорость будет у папы?
Тема 20. Измерение силы. §23
1. Что такое сила? Деформация тела.
Повторите из Темы 13 пункт 2 (Третий закон Ньютона), что такое сила.
По учебнику на стр.54 в §23 рассмотрите рис.54, где мальчик толкает тележку. В физике говорят, что на тележку действует сила. Мальчик играет роль силы.
Задание на уроке. 1. На стр.55 на всех рис.55-60 найдите тело, на которое действует сила, и тело, которое играет роль силы.
Опр. Силой наз. действие другого тела на данное тело. Сила - векторная физическая величина (имеет направление и измеряется в ньютонах).
Как узнают, что на тело действует сила (два способа)?
1. Если на тело действует сила, то данное тело изменяет свою скорость (но если не мешают другие тела!). Например, на рис.54 мальчик толкает тележку и, если трение не мешает, то тележка по 2-ому закону Ньютона начинает катиться всё быстрее и быстрее.
2. Если на тело действует сила, то тело изменяет свою форму и размеры - деформируется. Например, если ракеткой ударить по мячу (рис.57), то ракетка и мяч изменяют свою форму и размеры - деформируются, потому что оба тела по 3-ему закону Ньютона действуют друг на друга с равными силами.
Задание на уроке. 2. Объясните изменение скорости тел на рис.55-57 по 2-ому закону Ньютона и деформацию тел на рис.58-59 по 3-ему закону Ньютона.
Опр. Деформацией тела наз. изменение формы и размера тела.
Если тело изменило скорость или деформировалось, то на него обязательно подействовало другое тело, то есть сила!
2. Сила - векторная величина.
Физические величины бывают скалярными и векторными (повт. Тема 10, пункт 3). Например, масса тела - скалярная величина: она имеет только числовое значение: m = 5 кг. Сила - векторная величина. Это значит, что она имеет не только числовое значение F = 50 Н, но ещё направление и точку приложения.
Рассмотрим три примера, как под действием силы открывается дверь.
а) Маленькая сила F1 = 5 Н не откроет дверь, а сила F2 = 50 Н откроет. Значит, действие силы зависит от числового значения, или модуля силы.
б) Сила 50 Н, направленная вдоль двери, не откроет дверь, а направленная перпендикулярно двери - откроет. Действие силы зависит от направления.
в) Сила 50 Н, приложенная у ручки двери, откроет дверь, а приложенная около петель двери - не откроет. Действие силы зависит от точки приложения.
3. Измерение силы динамометром.
Для измерения силы используют прибор динамометр. В системе СИ сила измеряется в ньютонах, например, F = 10 Н.
Запомни: если к динамометру подвешен груз массой 102 г, то динамометр покажет 1 Н. Тело массой 1 кг весит почти 10 Н ( 9,8 Н).
Задание на уроке. 3. Прочитайте §28 стр.66 и ответьте на вопрос: "Какие бывают динамометры?" 4. Найдите цену деления и запишите показание динамометра с погрешностью в половину цены деления.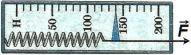
Цена деления: (150 - 100):5 = 10 Н.
Показание: F = 140 Н 5 Н.
4. По рисункам динамометров вычислите цену деления и запишите показания с учётом погрешности в 1 цену деления: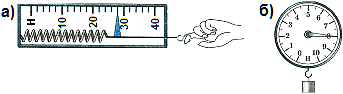
а) Цена деления: … ;
показание: F = … .
б) Цена деления: … ;
показание: F = … .
4. Изображение вектора силы. Масштаб.
Вектор силы изображают в виде отрезка со стрелкой на конце. Длину вектора будем брать от 2 см до 5 см, то есть от 4 клеток до 10 клеток. Для этого надо выбрать необходимый масштаб. Например, силу 40 Н удобно изобразить вектором длиной 4 клетки. Тогда масштаб будет 40 Н: 4 кл.= 10 Н в одной клетке. Если 40 Н: 8 кл.= 5 Н/кл. Если 40 Н: 5 кл.= 8 Н/кл.
Таким образом одну и ту же силу F = 40 Н можно начертить в трёх масштабах.
![]()
Чтобы выбрать масштаб силы, на силу разделить на целое число от 4 до 10.
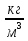 Задача 1. Человек тащит санки с силой 540 Н. Изобразите вектор силы.
Задача 1. Человек тащит санки с силой 540 Н. Изобразите вектор силы.
Решение. Среди чисел от 4 до 10 выбираем, например, число 6, т.к. 540 Н делится на 6. Чертим вектор длиной 6 клеток и пишем масштаб 90 Н/кл.
Задание на уроке. 5. Подберите масштаб вектора силы и начертите векторы сил: а) F = 12 Н; б) F = 80 Н; в) F = 360 Н. Подпишите силу и масштаб!
Все 3 вектора можно взять за 4 клетки, а можно а) - 6 кл.; б) - 8 кл.; в) - 9 кл.
5. Единицы измерения силы.
Гига
Мега
кило
1
милли
микро
миллиард
миллион
тысяча
1
тысячная
миллионная
1 ГН
1 МН
1 кН
1 Н
1 мН
1 мкН
1 000 000 000 Н
1 000 000 Н
1 000 Н
1 Н
0,001 Н
0,000 001 Н
9 цифр вправо
6 цифр
3 цифры
3 цифры
6 цифр влево
Запомни! "Кило" - это "тысяча". Напр., 5 килоньютон - это 5 тысяч ньютон.
Задание на уроке. 6. На оценку "3" преобразуйте значения сил в систему СИ:
а) 2 кН = … Н; б) 20 кН = … Н; в) 2,5 кН = … Н; г) 0,56 кН = … Н;
д) 12 000 мН = … Н; е) 240 мН = … Н; ж) 50 мН = … Н; з) 0,02 МН = … Н.
7. Выполни преобразование единиц силы.
а) 4 000 Н = … кН; б) 0,0035 Н = … мН; в) 20 000 000 Н = … МН;
г) 860 кН = … Н; д) 30 Н = … кН; е) 30 Н = … мН; ж) 0,6 ГН = … кН.
Дома: 1. Выучите Опр. силы и Опр. деформации в рамочках.
2. Какими двумя способами можно узнать, что на тело действует сила?
3. Какие три свойства имеет вектор силы? (Примеры с открыванием двери)
4. Подберите масштаб и начертите векторы сил:
а) F = 20 н; б) F = 35 Н; в) F = 240 Н; г) F = 420 Н.
5. Превратите единицы силы в систему СИ:
а) 5 кН = … Н; б) 120 кН = … Н; в) 3,5 кН = … Н; г) 0,45 кН = … Н;
д) 0,004 МН = … Н; е) 5 000 мН = … Н; ж) 350 мН = … Н.
Тема 21. Всемирное тяготение. Сила тяжести.
1. Явление всемирного тяготения.
Английский учёный Исаак Ньютон впервые догадался, что любые два тела во Вселенной притягиваются друг к другу с некоторой силой. Например, Луна притягивает Землю, а Земля притягивает Луну. Земля притягивает все тела на Земле. Два ученика притягивают друг друга, но эта сила ничтожно мала.
Опр. Всемирным тяготением наз. притяжение всех тел друг к другу.
Задание на уроке. 1. Прочитайте §24 стр.57 и ответьте на вопросы:
1) Почему листья падают на Землю? Почему течёт вода в реках?
2) Мяч бросили горизонтально. Почему он не летит прямолинейно?
3) Почему спутник вращается вокруг Земли, а Земля вокруг Солнца?
4) Два раза в сутки происходят приливы и отливы. Чем это объясняется?
Закон всемирного тяготения, открытый И. Ньютоном, гласит:
Любые два тела притягиваются друг к другу с некоторой силой. Чем больше массы тел, тем больше сила тяготения, а чем больше расстояние между ними, тем меньше сила тяготения.
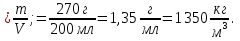 Чем больше масса тела m1 или тела m2, тем больше силы тяготения F1 и F2. А чем больше расстояние R между телами, тем силы тяготения меньше. По 3-ему закону Ньютона всегда F1 = F2.
Чем больше масса тела m1 или тела m2, тем больше силы тяготения F1 и F2. А чем больше расстояние R между телами, тем силы тяготения меньше. По 3-ему закону Ньютона всегда F1 = F2.
2. Сила тяжести.
На любое тело на Земле всегда действует сила притяжения Земли.
Опр. Силой тяжести наз. сила, с которой Земля притягивает тело.
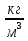 Силу тяжести обозначают Fтж. Вектор силы тяжести приложен к центру тяжести тела и направлен вертикально вниз. Чем больше масса тела, тем больше сила тяжести Fтж. Это значит, что сила тяжести прямо пропорциональна массе тела, где коэффициент пропорциональности g называют ускорением свободного падения. Если масса тела дана не точно (с одной верной цифрой), то коэффициент g можно брать округлённо g = 10 Н/кг.
Силу тяжести обозначают Fтж. Вектор силы тяжести приложен к центру тяжести тела и направлен вертикально вниз. Чем больше масса тела, тем больше сила тяжести Fтж. Это значит, что сила тяжести прямо пропорциональна массе тела, где коэффициент пропорциональности g называют ускорением свободного падения. Если масса тела дана не точно (с одной верной цифрой), то коэффициент g можно брать округлённо g = 10 Н/кг.
Задание на уроке. 2. Прочитайте §24 стр.58 и ответьте на вопросы:
1) Где сила тяжести больше: на полюсе или экваторе? Почему?
2) Одинакова ли сила тяжести у подножья горы и на вершине горы? Почему?
3) Почему на Луне человек легко смог бы перепрыгнуть через невысокий дом?
3. Решение задач на силу тяжести.
Задача 1. Найдите силу тяжести, действующую на мальчика массой 45 кг.
Дано:
Решение.
m = 45 кг
Fтж = mg; Fтж = 45 кг∙9,8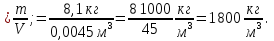 = 441 Н 440 Н.
= 441 Н 440 Н.
g = 9,8 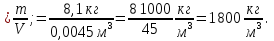
Fтж =?
Ответ. Fтж =440 Н.
Так как масса тела 45 кг дана с точностью до двух цифр, то и коэффициент g надо брать с точностью до двух цифр 0,98 (0 не считается!). Но часто при приближённом решении берут g = 10 Н/кг. Поэтому такую задачу считают устно: Fтж = mg = 45 кг∙10 Н/кг = 450 Н. Хотя ответ, как видим, отличается от 440 Н.
Задача 2. Найдите силу тяжести, действующую на тело массой 160 кг. Сделайте рисунок и покажите вектор силы тяжести. Подпишите масштаб.
Дано:
Решение.![]()
m = 160 кг
Fтж = mg; Fтж = 160 кг∙10 = 1 600 Н = 1,6 кН.
= 1 600 Н = 1,6 кН.
Масштаб: 1 600 Н : 4 кл = 400 Н/кл.
g = 10 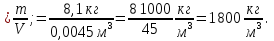
Fтж =?
Ответ. Fтж = 1,6 кН.
Задача 3. На тело действует сила тяжести 4,5 Н. Найти его массу в граммах.
Дано:
Решение.
Fтж = 4,5 Н
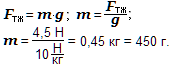
g = 10 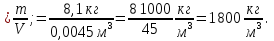
m - ?
Ответ. m = 450 г.
Задание на уроке. 3. Решите задачи на формулу силы тяжести (g = 10 Н/кг).
а) Найдите силу тяжести, действующую на тело массой 1,5 кг. Сделайте рисунок и покажите вектор силы тяжести. Подпишите масштаб.
б) На машину действует сила тяжести 45 кН. Найти его массу в тоннах.
Дома: 1. Выучите Опр всемирного тяготения и Закон всемирного тяготения!
2. Повторите ответы на вопросы к Заданиям на уроке 1 и 2.
3. Выучите Опр. силы тяжести, формулу, чертёж силы тяжести. Чему равно g?
4. Решите две задачи.
а) Найдите силу тяжести, действующую на тело массой 25 кг. Сделайте рисунок и покажите вектор силы тяжести. Подпишите масштаб.
б) На люстру действует сила тяжести 24 Н. Найти массу люстры.
Тема 22. Вес тела.
1. Вес тела.
Опр. Весом тела наз. сила, с которой тело действует на опору или подвес из-за притяжения Земли.
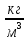
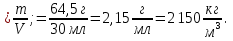 Вес тела обозначают Р. Вектор силы веса приложен к опоре или нижнему концу подвеса и направлен вниз. Если тело и опора (подвес) неподвижны или движутся прямолинейно и равномерно, то вес равен силе тяжести: Р = Fтж = m·g.
Вес тела обозначают Р. Вектор силы веса приложен к опоре или нижнему концу подвеса и направлен вниз. Если тело и опора (подвес) неподвижны или движутся прямолинейно и равномерно, то вес равен силе тяжести: Р = Fтж = m·g.
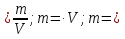 2. Задачи на силу тяжести и вес тела.
2. Задачи на силу тяжести и вес тела.
Задача 1. На столе стоит чайник с водой массой 1,5 кг. Определите силу тяжести и вес чайника. Покажите эти силы на рисунке. (См. на стр.64 рис.68 и пример).
Дано:
Решение.
m = 1,5 кг
Fтж = mg; Р = mg;
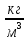
Масштаб: 15 Н : 5 кл = 3 Н/кл.
g = 10 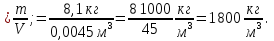
Fтж - ? Р - ?
Ответ. Fтж = 15 Н; Р = 15 Н.
Внимание! Нельзя путать понятия "вес тела" и "масса тела". Выражение "это тело весит 2 кг" недопустимо в физике, т.к. вес - это сила и измеряется в ньютонах. А в килограммах измеряется масса тела.
Нельзя путать также силу тяжести Fтж и вес тела Р. С силой тяжести Земля притягивает тело и эта сила приложена к центру тела. А с силой веса тело действует на опору, поэтому вес тела приложен к опоре (или подвесу).
Задача 2. С какой силой вода объёмом 20 л давит на дно аквариума?
Дано:
СИ
Решение.
V = 20 л
0,02 м3
1) 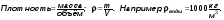 1 000
1 000  ∙0,02 м3 = 20 кг;
∙0,02 м3 = 20 кг;
2) Р = mg; Р = 20 кг∙10 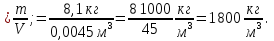 = 200 Н.
= 200 Н.
= 1 000 
g = 10 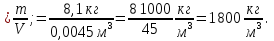
Р - ?
Ответ. Р = 200 Н.
Задание на уроке. 1. Решите задачи на силу тяжести и вес тела (на "3").
а) Телевизор массой 5,4 кг стоит на столе. Вычислите силу тяжести и вес телевизора. Покажите эти силы на двух отдельных рисунках в масштабе.
б) Лампа массой 400 г висит на потолке. Вычислите вес лампы и покажите вектор силы веса на рисунке в масштабе.
в) Какова масса человека весом 800 Н?
2. Каков вес подсолнечного масла в полной трёхлитровой банке?
Дома: 1. Выучите определение веса тела, формулу веса и оба рисунка.
2. На столе стоит чайник с водой массой 2,5 кг. Определите силу тяжести и вес чайника. Покажите эти силы на рисунке.
3. На нити висит алюминиевый шар объёмом 4 дм3. Найдите вес шара и покажите вектор силы веса на рисунке (в масштабе).
Тема 23. Сила упругости. Закон Гука.
1. Сила упругости.
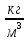 Опыт 1. На столе лежит книга. На книгу действует сила тяжести. По 2-ому закону Ньютона книга должна двигаться в направлении этой силы, т.е. вниз. Но книга покоится. Почему? Под действием книги стол немного деформировался (прогнулся). Деформированный стол действует на книгу снизу вверх: это сила упругости Fупр.
Опыт 1. На столе лежит книга. На книгу действует сила тяжести. По 2-ому закону Ньютона книга должна двигаться в направлении этой силы, т.е. вниз. Но книга покоится. Почему? Под действием книги стол немного деформировался (прогнулся). Деформированный стол действует на книгу снизу вверх: это сила упругости Fупр.
Сила упругости Fупруравновешивает (компенсирует) силу тяжести Fтж. Обе эти силы приложены к одному телу - книге, поэтому по 1-ому закону Ньютона книга покоится.
Опр. Силой упругости наз. сила, с которой деформированное тело действует на данное тело, вызвавшее деформацию.
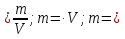 Книга действует на стол с силой своего веса Р. Стол в свою очередь действует на книгу с силой упругости Fупр. Это значит, что сила упругости Fупр противодействует весу тела Р по 3-ьему закону Ньютона, причём Fупр = Р.
Книга действует на стол с силой своего веса Р. Стол в свою очередь действует на книгу с силой упругости Fупр. Это значит, что сила упругости Fупр противодействует весу тела Р по 3-ьему закону Ньютона, причём Fупр = Р.
Что мы знаем про силу упругости Fупр:
1) Fупр возникает в деформированном теле;
2) Fупр действует на тело, которое вызвало деформацию.
2. Лабораторная работа №6. Градуирование пружины.
Задание на уроке. 1. Выполните лабораторную работу.
Эту работу выполним на уроке вместе с учителем. На каждом столе стоит штатив, в нём укреплён динамометр без шкалы (обёрнут чистой бумагой). Против указателя отметим штрих и напишем 0 Н.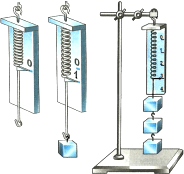
Будем по очереди подвешивать 1, 2, 3 и 4 гирьки по 100 г. Каждый раз против указателя отмечаем штрих и подписываем 1Н, 2Н, 3Н и 4Н. Измерим все промежутки между штрихами - они будут равны по 2,5 см. Промежутки между делениями разобьём сначала на 5 равных частей, а затем ещё пополам: получим шкалу с ценой деления 0,1 Н. Погрешность измерения будет равна половине цены деления: 0,05 Н.
Взвесим какое-нибудь тело и запишем его вес: Р = 2,7 0,05 Н. Оформите работу в Проверочной тетради на следующем уроке.
3. Закон Гука.
Выполняя лабораторную работу, мы заметили, что с каждой гирькой пружина удлинялась на одинаковую величину: 2,5 см. В растянутой (деформированной) пружине возникает сила упругости, которая приложена к гирькам и направлена вверх. Опыт показывает, что чем больше удлинение пружины, тем больше сила упругости. Этот закон впервые изучил английский учёный Роберт Гук.
Закон Гука. Сила упругости прямо пропорциональна удлинению тела.
Обозначим начальную длину пружины ℓо[м], конечную длину пружины ℓ [м], тогда удлинение пружины будет Δℓ = ℓ - ℓо. Из закона Гука следует, что сила упругости Fупр прямо пропорциональна удлинению пружины Δℓ. Коэффициент пропорциональности k называется жёсткостью пружины.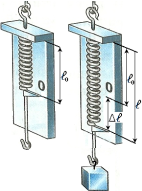
Формула закона Гука: Fупр = k·Δℓ., откуда жёсткость пружины k = 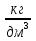
Задание на уроке. 2. Найдите в §25 на стр.60-61 ответы на следующие три вопроса:
1) Какие пять видов деформации бывают?
2) Какая деформация называется упругой?
3) Для какой деформации справедлив закон Гука?
Дома: 1. Выучите определение силы упругости. Книга покоится на столе. Какие две силы приложены к книге? Какими буквами они обозначаются?
2. Книга лежит на столе. Какие две силы противодействуют друг к другу? К каким телам они приложены? В каком теле Fупр возникла, а какому телу приложена?
3. Повторите из Темы 20, пункт 3 все Задания на уроке. 3. (С динамометрами)
4. Выучите закон Гука. Какими буквами обозначаются у пружины а) начальная длина; б) конечная длина; в) удлинение и г) жёсткость. Формула закона Гука!
Тема 24. Решение задач на закон Гука.
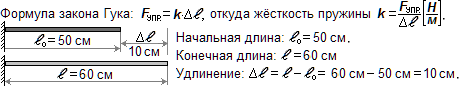
Задание на уроке. На рисунке изображён упругий резиновый шнур жёсткостью k [Н/м] с начальной длиной 50 см, который упруго удлинили на 10 см. При этом в шнуре возникла сила упругости Fупр. Разберите решения 4 задач.
Задача 1. Резиновый шнур жёсткостью 400 Н/м растянули на 10 см. Какая сила упругости возникнет в шнуре?
Дано:
СИ
Решение.
k = 400 Н/м
Fупр = k·Δℓ;
Fупр = 400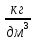 ∙ 0,1 м = 40 Н.
∙ 0,1 м = 40 Н.
Δℓ = 10 см
0,1 м
Fупр - ?
Ответ. Fупр = 40 Н.
Задача 2. Резиновый шнур растянули с силой 40 Н на 10 см. Найти жёсткость шнура.
Дано:
СИ
Решение.
Fупр = 40 Н
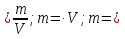
Δℓ = 10 см
0,1 м
k - ?
Ответ. k = 400 Н/м.
Задача 3 (на оценку "4"). Резиновый шнур длиной 50 см упруго растянули с силой 40 Н до длины 60 см. Найти жёсткость шнура.
Дано:
СИ
Решение.
Fупр = 40 Н
Δℓ = ℓ - ℓо = 0,6 м - 0,5 м = 0,1 м;
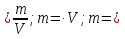
ℓо = 50 см
0,5 м
ℓ = 60 см
0,6 м
k - ?
Ответ. k = 400 Н/м.
Задача 4 (на оценку "5"). На сколько сантиметров удлинится стальная проволока жёсткостью 5 кН/м под действием груза 20 кг?
Дано:
СИ
Решение.
k = 5 кН/м
5 000 Н/м
Fупр = k·Δℓ, где Fупр = Fтж = m·g, откуда m·g = k·Δℓ.
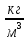
m = 20 кг
g = 10 Н/кг
Δℓ - ?
Ответ. Δℓ = 4 см.
Задание на уроке. Решите следующие 4 задачи.
5. Пружину жёсткостью 0,4 кН/м растянули на 2 см. Найти силу упругости.
6. Под действие груза 1 Н пружина растянулась на 2,5 см. Найти жёсткость.
7. К резинке жёсткостью 200 Н/м длиной 8 см подвесили груз. Под действием груза резинка стала длиной 10 см. Найти вес груза Р. (Учтите: Р = Fупр)
8. К резинке жёсткостью 200 Н/м длиной 8 см подвесили груз. Под действием груза резинка стала длиной 10 см. Найти массу груза.
Задачи на закон Гука (для контрольной работы).
Дома. Решите тот блок задач, который вам по силам. Но если не уверены в себе, то решите и предыдущий блок на более низкую оценку.
На оценку "3". №1. Найти силу упругости, если резинка жёсткостью 25 Н/м растянулась на 4 см. Отв. Fупр = 1 Н
№2. К лабораторному динамометру подвесили груз 3 Н, под действием которой пружина растянулась на 7,5 см. Найти жёсткость пружины. Отв. k = 40 Н/м
№3. На сколько сантиметров удлинится пружина жёсткостью 200 Н/м под действием груза 40 Н? Отв. Δℓ = 20 см
На оценку "4". №4. К стальной проволоке жёсткостью 2 кН/м подвесили груз, под действием которой она растянулась на 2,5 мм. Найти вес груза.
№5. К резинке жёсткостью 60 Н/м подвесили гирьку массой 300 г. На сколько сантиметров удлинится резинка?
№6. Под действием груза весом 40 Н резиновый шнур удлинился от 18 см до 20 см. Найти жёсткость шнура.
На оценку "5". №7. К резинке длиной 20 см жёсткостью 500 Н/м подвесили груз весом 10 Н. Найти конечную длину резинки.
№8. Пружина длиной 8 см под действием груза 200 г стала длиной 13 см. Найти жёсткость пружины.
Тема 25. Сложение сил. Равнодействующая. §29
Чаще всего на тело действует не одна сила, а сразу несколько сил. Например, на книгу, лежащую на столе, действуют две силы: Земля притягивает с силой Fтж вниз и стол действует с силой Fупр вверх. Эти силы компенсируют друг друга, как будто на книгу вообще не действует сила. Все силы, действующие на одно тело, можно сложить и заменить одной равнодействующей силой. Равнодействующая Fтж и Fупр равна нулю.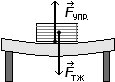
Опр. Равнодействующей силой наз. сила, которая оказывает на тело такое же действие, как и несколько одновременно действующих сил.
Силы складываются как векторы, но сложение векторов изучают в 9 классе. Поэтому рассмотрим правила сложения сил только для двух простых случаев.
1. Если две силы направлены в одну сторону, то равнодействующая этих сил равна сумме сил и направлена в ту же сторону.
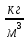
2. Если две силы направлены в противоположные стороны, то равнодействующая равна разности сил и направлена в сторону большей силы.
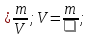
Задание на уроке. 1. Решите следующие 3 задачи по готовым чертежам.
а) Две гирьки 100 г и 200 г подвешены к общему подвесу. Найдите равнодействующую сил, приложенных к подвесу. (Используйте правило 1)
б) Кран равномерно поднимает на тросе груз 2 кН. Найдите равнодействующую сил, приложенных к грузу. (Используйте 1-ый закон Ньютона). Чему равен вес груза Р, к чему приложен вектор веса ![]() и куда направлен?
и куда направлен?
в) Кран поднимает груз весом 6 кН с силой 8 кН. (Используйте правило 2).
В каком направлении движется груз и под действием какой силы?
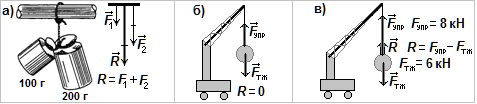
Задание на уроке. 2. Решите на стр.70 из Упражнения 11 задачи №1 и №3. Сделайте чертежи.
Дома. 1. Выучите Опр. равнодействующей силы и два правила в рамочках.
2. На оценку "3" решите три задачи а) и б) и в).
а) Снежинка равномерно падает. Начертите силы, действующие на снежинку. Чему равна равнодействующая этих сил?
б) Мальчик тащит санки с силой 150Н. Второй мальчик толкает санки сзади с силой 120 Н. Найти равнодействующую сил и сделать чертёж в масштабе.
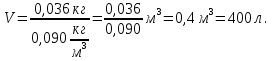 в) Найти равнодействующую двух сил, действующих
в) Найти равнодействующую двух сил, действующих
на тележку. В каком направлении будет двигаться те-
лежка: в направлении силы F1 или F2? (См. рисунок)
Дополнительные задания.
3. К телу приложены 4 силы: влево 5 Н, вверх 6 Н, вправо 5 Н и вниз 4 Н.
Найти равнодействующую всех сил. В каком направлении движется тело?
4. Штангист массой 70 кг пытается поднять с земли штангу массой 40 кг, прилагая силу 250 Н. С какой силой подошвы ног штангиста действуют на землю?
Задачи 3 и 4 выполните дома на листочке и на следующем уроке вложите в тетрадь для Проверочных работ.
Тема 26. Сила трения. §30, 31
1. Что такое сила трения? Две причины трения.
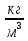 Когда одно тело движется по поверхности другого тела, возникает сила трения. Например, санки катятся вправо по поверхности дороги. Тогда неровности дороги цепляются за неровности полозьев санок, и дорога мешает двигаться санкам. Дорога действует на санки с силой трения, направленной влево, против движения санок. Говорят, что на санки действует сила трения Fтр.
Когда одно тело движется по поверхности другого тела, возникает сила трения. Например, санки катятся вправо по поверхности дороги. Тогда неровности дороги цепляются за неровности полозьев санок, и дорога мешает двигаться санкам. Дорога действует на санки с силой трения, направленной влево, против движения санок. Говорят, что на санки действует сила трения Fтр.
Опр. Силой трения наз. сила, с которой опора действует на движущееся тело, в сторону, противоположную движению тела.
Что нужно помнить про силу трения Fтр:
1) Fтр приложена к движущемуся телу (к санкам, а не к дороге);
2) Fтр направлена против движения тела.
Две причины трения.
а) Шероховатости опоры цепляются за шероховатости (неровности) тела. Чем более шероховатые поверхности, тем больше сила трения.
б) Наоборот, если обе соприкасающиеся поверхности очень гладкие, то сила трения будет большая уже из-за притяжения молекул. Например, лист стекла трудно сдвинуть по другому листу стекла, т.к. обе поверхности очень гладкие. Молекул располагаются очень близко и сильно притягиваются!
2. Как измерить силу трения? От чего зависит сила трения?
 Прицепим динамометр к бруску и будем таскать брусок с помощью динамометра, стараясь двигать брусок равномерно. Т.к. брусок движется равномерно, то по 1-ому закону Ньютона сила упругости Fупр пружины уравновешивает силу трения Fтр, значит, Fтр = Fупр. Поэтому динамометр показывает как силу упругости, так и силу трения. Например, на рис. Fупр динамометра 4 Н, тогда и Fтр = 4 Н.
Прицепим динамометр к бруску и будем таскать брусок с помощью динамометра, стараясь двигать брусок равномерно. Т.к. брусок движется равномерно, то по 1-ому закону Ньютона сила упругости Fупр пружины уравновешивает силу трения Fтр, значит, Fтр = Fупр. Поэтому динамометр показывает как силу упругости, так и силу трения. Например, на рис. Fупр динамометра 4 Н, тогда и Fтр = 4 Н.
От чего зависит сила трения?
а) Сила трения Fтр зависит от шероховатости соприкасающихся поверхностей (как опоры, так и движущегося тела): чем более гладкие поверхности, тем сила трения меньше. Но у слишком гладких поверхностей трение снова может увеличиться из-за притяжения молекул.
б) Ещё сила трения Fтр зависит от веса тела (или от силы, с которой тело прижимают к поверхности опоры). Например, если на брусок положить гирю или надавить сверху рукой, то сила трения увеличится.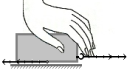
Чем больше сила, прижимающая тело к опоре, тем больше сила трения.
Внимание! Если кирпич тащить по поверхности стола на любой грани, то сила трения практически не изменится. Значит, сила трения не зависит от площади соприкасающихся поверхностей при одинаковой шероховатости.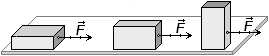
3. Три вида трения (скольжения, качения и покоя).
а) Трение скольжения: санки и лыжи скользят по снегу, коньки скользят по льду; транспорт при резком торможении скользит по асфальту (колёса не крутятся, а скользят юзом).
б) Трение качения: бревно или круглый камень катится с горы, транспорт катится на колёсах (но лыжи или коньки не катятся, а скользят!).
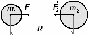 Будем тащить брусок по столу с помощью динамометра. Пусть, например, динамометр покажет силу трения скольжения 8 Н. Если брусок поставить на круглые палочки, то динамометр покажет силу трения качения всего 3 Н.
Будем тащить брусок по столу с помощью динамометра. Пусть, например, динамометр покажет силу трения скольжения 8 Н. Если брусок поставить на круглые палочки, то динамометр покажет силу трения качения всего 3 Н.
При одинаковой нагрузке сила трения качения меньше трения скольжения.
в) Трение покоя. Попытаемся сдвинуть с места тяжёлый шкаф. Если толкнуть с малой силой, то шкаф останется в покое. Значит, по 1-ому закону Ньютона сила трения пола на ножки шкафа Fтр уравновесило нашу силу F. Если толкнуть шкаф немного сильнее, то и сила трения покоя на ножки шкафа увеличится.
Т.к. шкаф остаётся в покое, то эту силу трения называют силой трения покоя.
Трение покоя играет очень важную роль в природе. Прежде всего, человек ходит благодаря трению покоя между подошвой и опорой. Также транспорт отталкивается от дороги благодаря трению покоя. Сила трения покоя удерживает на месте мебель в комнате, вбитые гвозди, узлы на верёвках, сшитые куски ткани и нити самой ткани (посмотри также стр.74 рис.81).
Задание на уроке. Прочитайте §31 (стр.73-74). Изучите рис.81 (транспортёр).
Дома. Прочитайте §30. Сила трения. Ответьте на все 8 вопросов на стр.73.
Тема 26 (Продолжение). Трение в природе и технике. §32
1. Как уменьшить вредное трение и увеличить полезное трение?
Вредное трение в технике уменьшают в основном тремя способами:
а) Трущиеся детали машин (поршень и цилиндр) обрабатывают - шлифуют, чтобы не было шероховатостей, делают гладкими.
б) Между трущимися поверхностями вводят жидкую смазку (машинное масло, солидол), потому что трение слоёв жидкости во много раз меньше, чем трение твёрдых поверхностей.
в) Для уменьшения трения вращающихся поверхностей (ось во втулке) используют подшипники. Подшипники бывают двух видов.

Подшипники качения имеют шарики или ролики, на которых вал совершает трение качения, которое в несколько раз меньше трения скольжения.
Подшипники скольжения имеют вкладыши, покрытые мягким металлом. Вал или ось опирается на вкладыш и вращается, совершая трение скольжения. Между вкладышами и вращающейся осью нужна хорошая смазка.
Полезное трение стремятся увеличить за счёт увеличения шероховатости поверхности: дороги посыпают песком, подошву обуви и шины автомобиля делают ребристыми, на гвозде делают засечки и шляпку гвоздя делают ребристой. Органы хватания у животных (хвосты обезьян, хоботы слонов) и растений (усики гороха, огурца) имеют шероховатую поверхность для увеличения трения покоя.
Задание на уроке. 1. Прочитайте §32. Ответьте на следующие вопросы:
а) Зачем в двигателе автомобиля тщательно шлифуют поршни и цилиндры?
б) Объясните, нужна ли смазка, если поверхности деталей отшлифованы.
в) Почему смазка уменьшает силу трения?
г) Где трение меньше: у подшипников качения или скольжения? Почему?
д) У обычного велосипеда имеется 6 пар шариковых подшипников. Можете назвать, где они установлены?
2. Распределите на две группы: а) полезное трение и б) вредное трение.
1. Человек идёт по асфальту. 2. Педаль велосипеда вращается.
3. Горох усиками цепляется за травинку. 4. Слон хоботом поднимает бревно.
5. Поршень движется по цилиндру. 6. Молотком бьют по шляпке гвоздя.
7. Шины автомобиля делают ребристыми. 8. Коньки затачивают.
3. На рисунке хоккейная шайба скользит по льду. Запишите в виде 4-значного числа (например, 4231), какими цифрами обозначены силы:
а) сила трения, б) сила тяжести,
в) сила упругости льда, г) вес шайбы.
Какие из этих сил приложены А) к шайбе: … (запишите цифрами); Б) ко льду: … (запишите цифрами).
4. Запишите значения сил упругости Fупр и трения Fтр с учётом погрешности, равной половине цены деления динамометра:
а) Fупр = … + … Н;
б) Fтр = … + … Н.
5. На рис. бруски А, Б и В одинаковы. Для какого тела сила трения будет наибольшая, а для какого наименьшая? Почему?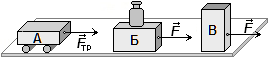
6. Распределите на три группы: а) трение скольжения, б) трение качения и в) трение покоя следующие примеры:
1. Лыжник катится с горы. 2. Колесо катится по дороге. 3. Человек идёт по полу.
4. Машина тормозит юзом. 5. Вагон движется по рельсам по инерции.
6. Тюк поднимают по наклонному транспортёру. 7. Вал по вкладышу.
Дома. 1. Выучите Опр. силы трения и два правила в рамочках.
2. На оценку "3" выучите ответы на вопросы:
а) Две причины трения. (Шероховатости поверхностей и притяжение молекул)
б) Как нужно двигать тело, чтобы измерить силу трения?
в) От чего зависит сила трения?
г) Назовите три вида трения. Назовите два вида подшипников.
д) Какими тремя способами можно уменьшить вредное трение?
3. Повторите все качественные задачи из этой темы.
Тема 27. Давление. Качественные задачи. §33, 34
1. Что такое давление? Единицы измерения давления.
Задача. На опоре площадью 6 м2 лежит груз весом 24 Н, а на опоре площадью 4 м2 лежит груз весом 20 Н. Какой груз глубже провалится в снегу?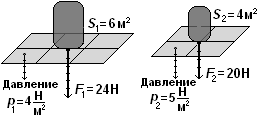
Очевидно, глубже провалится тот груз, где сила на 1 м2 будет больше.
У первого груза: 24 Н:6 м2 = 4 Н/м2.
У второго груза: 20 Н:4 м2 = 5 Н/м2.
Сила на 1 м2 называется давлением и обозначается буквой р.
Т.к. давление 4 Н/м2 < 5 Н/м2, то второй груз провалится глубже.
Опр. Давлением наз. отношение силы F, действующей перпендикулярно поверхности, к площади S этой поверхности.
Формула давления:  . В системе СИ давление измеряется в паскалях.
. В системе СИ давление измеряется в паскалях.
Запомни: р[Па] - давление; F[Н] - сила давления; S[м3].
Единица давления 1 Па = 1 Н/м2 названа в честь французского физика и математика Блеза Паскаля.
Давление 1 Па очень маленькое, поэтому миллипаскали применяются редко, зато часто применяются гектопаскали и килопаскали.
Гига
Мега
кило
гекто
1
миллиард
миллион
тысяча
сто
1
1 ГПа
1 МПа
1 кПа
1 гПа
1 Па
1 000 000 000 Па
1 000 000 Па
1 000 Па
100 Па
1 Па
9 цифр вправо
6 цифр
3 цифры
2 цифры
Задание на уроке. 1. Выполни преобразование единиц давления.
а) 100 кПа =…Па; б) 120 000 Па =…кПа; в) 0,98 кПа =…Па; г) 60 000 Па =…кПа;
д) 1 100 гПа =…Па; е) 320 000 Па =…гПа; ж) 480 гПа =…Па; з) 4 500 Па =…гПа;
и) 0,06 МПа =…Па; к) 6 000 000 Па =…МПа; л) 0,3 МПа =…кПа; м) 0,01 ГПа =…Па.
2. Зависимость давления от силы и площади опоры.
Не путайте физические величины давление р [Па] и силу давления F [H].
а) Как зависит давление р от силы давления F?
По формуле 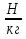 видно, что чем больше числитель F, тем больше и дробь, а значит, тем больше давление р (если площадь S не изменяется).
видно, что чем больше числитель F, тем больше и дробь, а значит, тем больше давление р (если площадь S не изменяется).
б) Как зависит давление р от площади опоры S?
По формуле видно, чем больше знаменатель S, тем меньше дробь и тем меньше давление р (если сила F постоянная).
Давление р прямо пропорционально силе F и обратно пропорционально площади опоры S.
Задание на уроке. 2. Качественные задачи на давление.
а) Зачем фундамент здания всегда делают шире, чем стены?
- Чтобы площадь S фундамента была больше, тогда давление р на почву будет меньше, и здание не будет проваливаться.
б) Зачем лезвия режущих и острия колющих инструментов оттачивают?
- Чтобы их площадь S была меньше, тогда давление р будет больше, и с инструментом легче работать.
в) Зачем при бороновании плотной почвы на борону кладут бревно?
- Чтобы увеличить силу давления F, тогда давление р будет больше, и зубья бороны глубже заходят в почву.
г) Зависит ли давление кирпича на стол от того, какой гранью он лежит на столе?
- Да, зависит. Чем площадь S грани больше, тем давление р меньше.
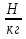 д) Какой лопатой легче копать: А или Б?
д) Какой лопатой легче копать: А или Б?
- Легче копать лопатой Б, потому что у неё меньше площадь острия, поэтому давление больше.
е) Аист стоял на двух ногах, потом одну ногу поджал. Изменилось ли давление аиста на землю?
- Да, изменилось. Так как площадь опоры стала меньше в 2 раза, то давление увеличилось в 2 раза. Аист на одной ноге глубже проваливается в почву.
ж) При вытаскивания гвоздя из стены гвоздодёром остаётся вмятина от гвоздодёра. Предложите способ избежать этой вмятины.
Задание на уроке. 3. Прочитайте на стр.80-81 §34 и ответьте на вопросы:
а) Почему шины грузовых автомобилей и шасси самолётов делают широкими?
б) Что больше: давление острия кнопки или давление гусеничного трактора?
в) Какие режущие и колющие приспособления встречаются в живой природе?
(Для учителя: если Задание 3 не успеете на уроке, то задать домой на "4")
Дома. 1. Выучите Опр. давления и правило в рамочке.
2. На оценку "3" преобразуйте единицы давления (обязательно уметь всё!),
а) 2 кПа = … Па; б) 120 кПа = … Па; в) 12,5 кПа = … Па; г) 0,045 кПа = … Па;
д) 3 000 Па = … кПа; е) 65 200 Па = … кПа; ж) 1 200 000 Па = … МПа;
з) 0,04 МПа = … Па; и) 76 гПа = … Па; к) 6 450 Па = … гПа.
3. Повторите качественные задачи, решённые на уроке.
Тема 28. Давление. Количественные задачи. §33
1. Единицы длины ℓ, площади S и объёма V.
В единицах длины ℓ при переходе к соседней величине запятая переносится на 1 цифру, в единицах площади S - на 2 цифры, в единицах объёма - на 3 цифры.
1 м ← 1 дм ← 1 см; 1 м2 ←← 1 дм2 ←← 1 см2; 1 м3 ←←← 1 дм3 ←←← 1 см3.
Задание на уроке. 1. Разберитесь, как превращают в систему СИ единицы
длины: а) 5 дм = 0,5 м; б) 154 дм = 15,4 м; в) 20 см = 0,2 м; г) 250 см = 2,5 м;
площади: а) 5 дм2 = 0,05 м2; б) 200 дм2 = 2 м2; в) 250 см2 = 0,025 м2;
объёма: а) 5 дм3 = 0,005 м3; б) 500 дм3 = 0,5 м3; в) 25 000 см3 = 0,025 м3.
Задание на уроке. 2. Превратите в систему СИ единицы площади:
а) 8 дм2 = … м2; б) 160 дм2 = … м2; в) 200 дм2 = … м2; г) 0,6 дм2 = … м2;
д) 160 см2 = … м2; е) 40 000 см2 = … м2; ж) 1 500 см2 = … м2; з) 20 см2 = … м2.
2. Задачи на вычисление давления.
Задача 1. Бак весом 12 кН лежит на опоре площадью 0,6 м2. Найти давление.
Дано:
СИ
Решение.
F = 12 кН
12 000 Н
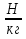
S = 0,6 м2
р - ?
Ответ. р = 20 кПа.
Задача 2. Вычислите давление на стол кирпича массой 6 кг на грань размерами 30 см 16 см. (Решим задачу по действиям - на оценку "4")
Дано:
СИ
Решение.
m = 6 кг
1) Найдём площадь: S = a∙b; S = 0,3 м∙0,16 м = 0,048 м2;
2) Найдём вес тела: Р = mg; P = 6 кг∙10 Н/кг = 60 Н;
3) Найдём давление:
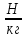
а = 30 см
b = 16 см
g = 10 Н/кг
0,3 м
0,16 м
р - ?
Ответ. р = 1,25 кПа.
На оценку "5" Задачу 2 надо уметь решать с помощью расчётной формулы.
Дано:
СИ
Решение.
m = 6 кг
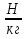
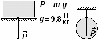
Ответ. р = 1,25 кПа.
а = 30 см
b = 16 см
g = 10 Н/кг
0,3 м
0,16 м
р - ?
При вычислении по расчётной формуле единицу измерения пишут лишь в конце
Задание на уроке. 2. Решите задачи а) и б) на вычисление давления по действиям, а потом получите ещё и расчётную формулу.
а) Какое давление оказывает 16 кг воды на дно аквариума площадью 80 дм2?
б) Какое давление оказывает песок весом 4,8 кН на дно ящика размерами 80 см на 30 см? Ответ выразите в килопаскалях.
3. Задачи на вычисление силы давления F и площади S.
Задача 3. Известно, что давление воздуха 100 кПа. Найдите силу давления воздуха на стол площадью 150 дм2.
Дано:
СИ
Решение.
р = 100 кПа
S = 150 дм2
100 000 Па
1,5 м2
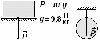
F = 100 000 Па∙1,5 м2 = 150 000 Н = 150 кН.
F - ?
Ответ. F = 150 кН.
Задача 4. Гусеничный трактор весом 42 кН оказывает на почву давление 30 кПа. Найти площадь гусениц трактора.
Дано:
СИ
Решение.
F = 42 кН
р = 30 кПа
42 000 Н
30 000 Па

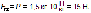
S - ?
Ответ. F = 150 кН.
Задание на уроке. 3. Решите задачи а) и б) на вычисление силы давления и площади - на оценку "3" обязательно уметь решать.
а) Снег оказывает на крышу площадью 6 м2 давление 12 кПа. Найти вес снега.
б) Мальчик весом 400 Н на лыжах оказывает давление 8 кПа. Найдите площадь лыж. В ответе площадь запишите в квадратных дециметрах.
Дома. Решите один из блоков задач, который вам по силам.
На оценку "3". (Если выбрали этот блок, то все 3 задачи надо решить верно)
1. На крыше площадью 1,2 м2 лежит снег весом 24 кН. Найти давление снега.
2. Площадь дна аквариума 40 дм2. Давление воды на дно 6 кПа. Найти вес воды в аквариуме.
3. Мальчик весом 450 Н оказывает давление на пол 15 кПа. Найти площадь подошв ботинок. Выразите площадь в квадратных дециметрах.
На оценку "4". (Если из этого блока верно решены 2 задачи, то оценка "3")
4. Снегоход массой 320 кг имеет гусеницы площадью 80 дм2. Найти давление снегохода на снег.
5. Найти вес песка в кузове автомобиля длиной 2,5 м и шириной 1,6 м, если давление песка на дно кузова 24 кПа.
6. Кирпич массой 6 кг создаёт давление на стол 1,2 кПа. Найти площадь основания кирпича.
На оценку "5". 7. Найти давление бруска 600 г на грань площадью 400 см2.
8. На дно аквариума размерами 4 дмХ5дм вода оказывает давление 0,72 кПа. Найти вес воды в аквариуме.
9. Давление Юры массой 40 кг на пол равна 16 кПа. Найти площадь обуви в дм2.
Учебный год
Фамилия Имя ученика
2014-2015
2015-2016
2016-2017
2017-2018
Физика 7 класс
Часть 1
Учитель физики МКОУ "Гауфская СОШ»
Тугеус В.Я.
д.Гауф - 2014 год
Тема 29. Давление газа. §35
1. Как создаётся давление газа?
Газ в закрытом сосуде оказывает давление на все стенки сосуда. Это давление объясняется тем, что молекулы газа ударяются о стенки сосуда. Точно также газ оказывает давление на любое тело, находящееся в газе.
Давление газа на стенки сосуда и на тела, находящиеся в газе, вызывается ударами молекул газа.
Задание на уроке. 1. Под стеклянный колокол помещают завязанный воздушный шар, содержащий немного воздуха. Через отверстие на дне колокола начинают выкачивать воздух. Шарик начинает надуваться. Объясните опыт.
2. Как давление газа зависит от объёма газа?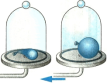
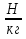 Возьмём газ в цилиндре, закрытом сверху подвижным поршнем. Если с помощью поршня уменьшить объём газа (сжать газ), то давление газа в цилиндре увеличится, потому что молекулы газа будут чаще ударяться об стенки сосуда.
Возьмём газ в цилиндре, закрытом сверху подвижным поршнем. Если с помощью поршня уменьшить объём газа (сжать газ), то давление газа в цилиндре увеличится, потому что молекулы газа будут чаще ударяться об стенки сосуда.
Это свойство газа изучили немец Роберт Бойль и француз Мариотт. они открыли закон зависимости давления газа р от объёма газа V.
Закон Бойля-Мариотта. Во сколько раз уменьшится объём газа, во столько же раз увеличится давление (если не менять температуру).
По-другому: давление газа обратно пропорционально объёму газа.
Задание на уроке. 2. Разберите решение качественных задач.
а) В цилиндре газ был под давлением 90 кПа. Под действием поршня объём газа уменьшили в 3 раза. Каким стало давление газа в цилиндре?
Решение. Т.к. объём уменьшили в 3 раза, то давление увеличится в 3 раза и станет 90 кПа∙3 = 270 кПа.
б) Два одинаковых сосуда соединены шлангом, кран К![]()
закрыт. В левом сосуде газ находится под давлением,
а правый сосуд пустой. Каким будет давление, когда кран откроют?
Решение. Если открыть кран, то объём увеличится в 2 раза, тогда давление газа уменьшится в 2 раза и станет 40 кПа : 2 = 20 кПа.
в) В баллоне объёмом 1 л и в баллоне объёмом 3 л находится одинаковая масса газа. Сравните давление газа в сосудах. Решите самостоятельно.
г) В сосуде объёмом 8 л давление было 100 кПа. Какое будет давление этой же массы газа, если объём станет 2,5 л?
Дано: Решение.
V1 = 8 л 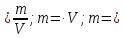
р1 = 100 кПа
V2 = 2,5 л
р2 - ? Ответ. р2 = 320 кПа.
3. Как давление газа зависит от температуры? Закон Шарля.
Если газ нагревать в закрытом сосуде, то давление газа будет увеличиваться. Баллон с газом может даже разорваться! Это происходит потому, что при нагревании скорость молекул газа увеличивается, поэтому молекулы будут ударяться о стенки сосуда чаще и сильнее.
Это свойство газа изучил француз Шарль.
Закон Шарля. Чем больше температура газа в закрытом сосуде, тем больше давление газа.
Задание на уроке. 3. Решите задачи.
а) В двух одинаковых баллонах находится одинаковая масса газа. Один баллон находится в тёплой комнате, а другой - на морозе. Сравните давление газа в баллонах.
б) Возьмите холодную бутылку руками и опустите горлышко под воду: из бутылки будут выходить пузырьки воздуха. Почему? (Проделайте опыт в классе)
в) Давление газа в цилиндре под поршнем увеличили от 100 кПа до 250 кПа. Объём газа был 50 мл. Каким станет объём газа?
Дома: 1. На оценку "3" выучите все три правила в рамочках и повторите качественные задачи, решённые на уроке.
2. Решите задачу на закон Бойля-Мариотта. В сосуде объёмом 5 л давление было 80 кПа. Какое будет давление этой же массы газа при объёме 4 л?
3. Прочитайте по учебнику §35 и ответьте на вопросы: а) Что будет с резиновой плёнкой на конце цилиндра А, если нажать на поршень? А если вытянуть поршень, как на рис. Б?
б) Где используются баллоны со сжатым газом? Приведите примеры.
Тема 30. Закон Паскаля. Давление в жидкости. §36, 37
1. Закон Паскаля.
Газ занимает весь сосуд и очень подвижен. Если нажать пальцем на мяч, то от стенки мяча молекулы воздуха получат удар. Но так как молекулы воздуха очень подвижны, то этот удар тут же передаётся соседним молекулам по всему мячу. Во всём мяче тут же давление воздуха немного увеличится.
Это свойство газа изучил француз Блез Паскаль. Таким же свойством обладают и жидкости.
Закон Паскаля. Давление на жидкость или газ передаётся одинаково во всех направлениях жидкости или газа.
Справедливость закона Паскаля можно наблюдать на опыте с шаром Паскаля. Шар с отверстиями наполняют либо газом (дым) либо жидкостью. При нажатии на поршень струйки дыма или воды вылетают во все отверстия одинаково.
Задание на уроке. 1. Решите качественные задачи.
а) Когда выдавливают пасту из тюбика, каким законом физики пользуются?
б) Если из мелкокалиберной винтовки выстрелить в варёное яйцо, в нём образуется отверстие. Если же выстрелить в сырое яйцо, оно разлетится. Почему?
4. Опыты на изучение давления в жидкости.
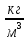 Опыт 1. Нижний конец стеклянной трубки закроем резиновой плёнкой и нальём воды. Под действием силы тяжести воды плёнка прогнётся. Сила упругости плёнки уравновесит силу тяжести воды: Fтж = Fупр. Вывод: чем выше столб воды, тем больше давление воды на резиновую плёнку.
Опыт 1. Нижний конец стеклянной трубки закроем резиновой плёнкой и нальём воды. Под действием силы тяжести воды плёнка прогнётся. Сила упругости плёнки уравновесит силу тяжести воды: Fтж = Fупр. Вывод: чем выше столб воды, тем больше давление воды на резиновую плёнку.
Опыт 2. Этот опыт вы можете посмотреть в классе. Плоская коробочка с одной стороны обтянута резиновой плёнкой, с другой стороны соединена резиновой трубочкой с водяным манометром. Если надавить на резиновую плёнку, то воздух в коробочке сожмётся и надавит на жидкость в манометре.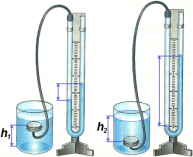
На одной и той же глубине манометр покажет одинаковое давление. Чем глубже опустить в воду коробочку с резиновой плёнкой, тем большее давление покажет манометр. В следующей теме мы выведем формулу давления в жидкости. Пока запомним такой вывод:
Внутри жидкости есть давление, которое на одной и той же глубине по всем направлениям одинаково, а чем глубина больше, тем давление больше.
Задание на уроке. 2. Решите качественные задачи.
а) Питьевой бачок с водой имеет в нижней части краник. Почему при полном бачке вода из краника бежит быстрее, чем при полупустом?
б) Почему пловец, нырнувший на большую глубину, испытывает боль в ушах?
в) Со дна водоёма поднимается пузырёк газа. Сохраняется ли при этом объём?
3. Воздух под поршнем в закрытом сосуде сжимают. Как при этом меняются: А) масса воздуха; Б) объём воздуха; В) плотность воздуха;
Г) давление воздуха; Д) сила тяжести, действующая на воздух.
1) Уменьшается; 2) увеличивается; 3) не изменяется.
Ответ запишите в виде числа из 5 цифр, например: 2 1 1 3 2.
Подобные задания есть в экзамене ГИА в 9 классе.
4. Из шара Паскаля под давлением вылетают три струйки воды: вверх, в сторону и вниз. Почему при небольшом нажатии нижняя струйка будет заметно сильнее? Выполняется ли закон Паскаля? Какими будут струйки газа?
Решение. Давление от поршня распределится во все стороны одинаково - закон Паскаля выполняется. Но на нижнее отверстие дополнительно давит ещё столб воды внутри шара. Если шар наполнен газом, то все струйки будут одинаковы, т.к. столб газа весит ничтожно мало.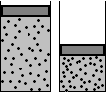
Дома: 1. На оценку "3" выучите закон Паскаля и правило в рамочке. Повторите качественные задачи, решённые на уроке.
2. Два сосуда соединены открытой трубкой. В левом сосуде давление газа 60 кПа. Объём правого сосуда в 3 раза меньше. Какое давление правом сосуде?
3. Задача на закон Бойля-Мариотта. Давление газа в цилиндре было 60 кПа. Каким станет давление газа, если объём уменьшится в 3 раза?![]()
Тема 31. Решение задач на давление в жидкости. §38
1. Вывод формулы давления в жидкости на глубине h.
Чтобы вывести формулу давления жидкости на дно сосуда, воспользуемся определением давления: 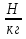 .
.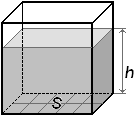
Сила F в числителе - это вес, с которой жидкость давит на дно сосуда: F = P = mg, где массу жидкости найдём из определения плотности: 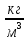 , откуда m = ρ·V.
, откуда m = ρ·V.
Тогда F = mg = ρ·V·g. Объём сосуда V = S·h. Тогда получим F = ρ·Sh·g. Вернёмся к формуле определения давления: 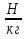 Получаем формулу: p = gρh..
Получаем формулу: p = gρh..
Впервые в физике вы встретились с выводом формулы. В старших классах вы это будете делать часто. На оценку "5" за четверть вывод надо знать!
На "3" надо обязательно знать буквы в формуле (выучите наизусть!):
р[Па] - давление; g = 10 Н/кг; [кг/м3] - плотность жидкости; h[м] - глубина.
По формуле видно, что давление р на дно жидкости прямо пропорционально плотности жидкости ρ·и прямо пропорционально высоте столба жидкости h. По этой же формуле вычисляют давление р на стенки сосуда на глубине h.
2. Задачи на расчёт давления в жидкости.
Задача 1. Вычислите давление воды в аквариуме на глубине 40 см. (Плотность воды надо знать наизусть 1 000 кг/м3. Не забудьте g = 10 Н/кг.)
Дано:
СИ
Решение.
h = 40 см
= 1 000 кг/м3
g = 10 Н/кг
0,4 м
р = g h;
р = 10 н/кг∙1 000 кг/м3∙0,4 м = 4 000 Н = 4 кН.
Ответ. р = 4 кН.
р - ?
Задача 2. Какой высоты столб воды создаёт давление, равное атмосферному давлению 100 кПа?
Дано:
СИ
Решение.
р = 100 кП
= 1 000 кг/м3
g = 10 Н/кг
100 000 Па
Ответ. h = 10 м.
h - ?
Задача 3. С какой силой давит серная кислота на пробку площадью 35 см2 в цистерне с кислотой на глубине 2 м 50 см? (Плотность на стр.51 учебника)
Дано:
СИ
Решение.
S = 35 см2
h = 2м 50 см
g = 10 Н/кг
= 1 800 кг/м3
0,0035 м2
2,5 м
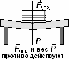
F = 10 Н/кг·1800 кг/м3·2,5 м·0,0035 м2 =
=157,5 Н ≈ 160 Н.
Ответ. F = 160 Н.
F - ?
Эта задача решена с помощью получения расчётной формулы: F = g hS.
Внимание! Расчётные формулы в решении надо обязательно вывести! Если вы просто запомнили расчётную формулу и решили по ней задачу, то такое решение не засчитывается! Уж лучше решить задачу по действиям!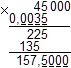
1) Давление р = gh = 10 Н/кг∙1 800 кг/м3∙2,5 м = 45 000 Па;
![]()
Задача 4. Какую жидкость надо налить в бочку, чтобы при высоте жидкости 2 м на дно бочки площадью 3 м2 действовала бы сила 60 кН?
Дано: СИ Решение.
h = 2 м 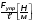
S = 3 м3
F = 60 кН 60 000 Н
g = 10 Н/кг
ρ - ? Ответ. ρ = 1 000 кг/м3 - вода.
Задание на уроке. Решите задачи. Плотности жидкостей берите на стр.51.
1. Вычислите в килопаскалях давление мёда на дно банки глубиной 20 см.
2. Давление на дно цистерны с нефтью равно 20 кПа. Найдите глубину нефти.
3. Найдите вес воды в аквариуме с основанием 15 дм2 и высотой воды 40 см.
Дома. Решите один из блоков задач, который вам по силам.
На оценку "3". (Если выбрали этот блок, то задачи 1 и 2 надо решить верно)
1. Найдите давление в керосине на глубине 50 см. Выразите в килопаскалях.
2. Какой высоты был налит в канистру керосин, если его давление на дно 4 кПа?
3. С какой силой давит керосин на пробку площадью 20 см2 в цистерне с керосином на глубине 2 м? Решите по действиям!
На оценку "4". (Если из этого блока верно решены 1-2 задачи, то оценка "3")
1. Вычислите давление на дно Марианской впадины в Тихом океане на глубине 10 900 м. Плотность морской воды 1 030 кг/м3. Округлите до целых МПа.
2. Столб дизельного топлива высотой 20 см оказывает давление в 1,72 кПа на дно сосуда. Какова плотность дизельного топлива?
3. Определите силу давления на маску аквалангиста при его погружении на глубину 20 м, если площадь маски 120 см2.
На оценку "5".
1. Вычислите давление на дно Марианской впадины в Тихом океане на глубине 10,9 км. Плотность морской воды 1 030 кг/м3. Округлите до целых МПа.
2. Какая жидкость налита в мензурку, если столб жидкости высотой 20 см оказывает давление 3,6 кПа? Найдите жидкость с такой плотностью на стр.51.
3. Брусок с площадью основания 100 см2 и высотой 20 см находится под водой на глубине 80 см от верхнего основания. Найти силу давления F1 на верхнее основание и F2 на нижнее основание, также их равнодействующую R.
Дополнительное задание. Гидростатический парадокс.
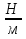 Прочитай на стр.176-178 §4. На рисунке даны три сосуда, у которых на дне отверстия одинаковой площади затянуты резиновой плёнкой. Уровни воды в сосудах не одинаковы. В каком сосуде плёнка испытывает наибольшее давление? Почему?
Прочитай на стр.176-178 §4. На рисунке даны три сосуда, у которых на дне отверстия одинаковой площади затянуты резиновой плёнкой. Уровни воды в сосудах не одинаковы. В каком сосуде плёнка испытывает наибольшее давление? Почему?
Тема 32. Сообщающиеся сосуды. §39
1. Сообщающиеся сосуды с однородной жидкостью.
Задание на уроке. 1. Прочитайте §39 стр.93, рассмотрите опыты на рис.107 и рис.109 (эти опыты также показывает учитель в классе). Запомните вывод:
В сообщающихся сосудах любой формы однородная жидкость будет на одном уровне, если давление воздуха над жидкостью одинаково.
Задача 1. В средний сосуд налили воды до высоты h.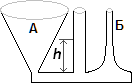
Какой высоты будет столб воды в соседних сосудах: больше, меньше или равно h?
Решение. Т.к. сосуды сверху открыты, то давление воздуха одинаково. Тогда по закону сообщающихся сосудов высота однородной жидкости в сосудах А и Б тоже будет равна h.
Задание на уроке. 2. Подумайте, как будет проходить наивысший уровень воды при наклонном расположении сосуда (см. рис.). А потом проверьте в классе опытным путём свою гипотезу.
Проведите горизонтальные прямые через точки А, Б и В.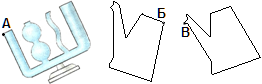
Задача 2. Левое колено А закрыто сверху. Когда в правое колено Б налили воды, то уровень воды в колене Б оказался выше. Почему?
Решение. Потому что в левом колене А находится сжатый воздух, который оказывает на воду большее давление, чем давление воздуха на воду в открытом колене Б.
Задание на уроке. 3. Решите качественные задачи (ответ и обоснование).
а) В какой чайник можно набрать больше воды: в А, в Б или одинаково.
Если открыть кран К, то куда потечёт жидкость: влево, вправо или не потечёт.

4. На стр.95 из Упражнения 16 разберите задачу 1 про водомерное стекло и задачу 2 про артезианский колодец.
5. На стр.96 из Задания 9 решите задание 2 о работе шлюзов (есть плакат).
2. Сообщающиеся сосуды с жидкостью разной плотности.
Нальём в U-образный сосуд воды, а потом в левое колено керосина. Вода и керосин не смешиваются. Т.к. плотность керосина ρ1 = 0,8 г/см3меньше плотности воды ρ1 = 1 г/см3, то высота столба керосина h1больше высоты столба воды h2, тогда давление на уровне АБ будет одинаково: р1 = р2.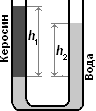
Т.к. р1 = gρ1h1 и р2 = gρ2h2, то gρ1h1 = gρ2h2. Отсюда: ρ1h1 = = ρ2h2. Соберём ρ1 и ρ2 слева, а h1 и h2 справа: 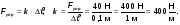
При равенстве давлений высота столба жидкости обратно пропорциональна плотности жидкости.
Две трудные задачи на оценку "5".
Задача 3. В U-образный сосуд налили воды, а потом в левое колено керосина высотой 50 см. На сколько см уровень столба керосина будет выше уровня воды? (См. чертёж на предыдущей странице).
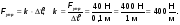 Дано: Решение.
Дано: Решение.
ρ1= 0,8 г/см3
h1 = 50 см
ρ2 = 1 г/см3
∆h - ? ∆h = h1 - h2 =
= 50 см - 40 см = 10 см. Ответ. ∆h = 10 см.
Задача 4. Медицинская грелка с водой соединена с вертикальной стеклянной трубкой. На грелку положили лёгкую картонку, на неё гирю 5 кг. Вода по трубке поднялась на 1 м. Найти площадь соприкосновения картонки с грелкой.
Дано: m = 5 кг; h = 1 м; g = 10 Н/кг; = 1000 кг/м3.
Найти: S - ?
Решение. По опр. давления: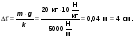

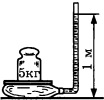
Дома. 1. На оценку "3" выучите правило сообщающихся сосудов в рамочке и повторите качественные задачи из пункта 1. Сообщающиеся сосуды с однородной жидкостью.
2. На оценку "5" уметь вывести формулу для жидкостей с разной плотностью.
3. Решите на листочке задачи на "4" и "5" и принесите к уроку.
а) В U-образную трубку налили сперва много воды, а потом в левое колено немного тяжёлой жидкости плотностью 1 600 кг/м3 высотой 5 см. На сколько сантиметров столб воды будет выше? Сделайте рисунок!
б) Человек массой 75 кг стоит на резиновом мешке с водой на фанерке площадью 10 дм2. На сколько см поднимется вода по стеклянной трубке, прикреплённой к резиновому мешку?
Тема 33. Атмосферное давление. §40, 42
1. Вес воздуха - причина атмосферного давления.
Атмосферой наз. воздушная оболочка вокруг Земли (вокруг других планет). Земля притягивает воздух, т.е. на воздух действует сила тяжести. Из-за этого воздух давит на поверхность Земли, т.е. воздух имеет вес. Вес воздуха можно вычислить по формуле Р = mg [Н], если известна масса m[кг].
Задание на уроке. 1. Прочитайте на стр.97 §40 опыт по измерению массы воздуха в стеклянной колбе (рис.115). Запомните: что при нормальном атмосферном давлении плотность воздуха в = 1,29 кг/м3 1,3 кг/м3. По сравнению с водой воздух в 775 раз легче. Смогли бы вы "поднять" воздух кабинета физики?
Задача 1. Найти массу воздуха в кабинете физики размерами 3 м х 6 м х 13м.
Дано: Решение.
a = 3 м 
b = 6 м
c = 13 м m = 1,3 кг/м3·3 м·6 м·13 м = 304 кг.
ρ = 1,3 кг/м3
m - ? Ответ. m = 304 кг.
Воздух весит не так уж и мало! Недаром ураган производит такие сильные разрушения. А с какой силой атмосфера давит на поверхность земли?
2. Что такое атмосферное давление. Качественные задачи.
Задание на уроке. 2. Прочитайте на стр.95 вторую половину §40. Разберитесь, как создаётся атмосферное давление на Земле. Разберитесь с решением качественных задач на рис.116 и на рис.117. Решение качественных задач:
а) Почему при всасывании через трубочку сок поднимается из стакана по трубочке вверх против силы тяжести? (Выучите решение этой задачи!)
Решение. Потому что в трубочке над соком давление воздуха мы уменьшаем, а атмосфера давит на сок в стакане и поднимает его вверх по трубочке.
б) Объясните работу медицинского шприца.
Решение. 1) Если иглу опустить в жидкость и поднимать поршень шприца, то жидкость набирается в шприц под действием атмосферного давления на поверхность жидкости. 2) Если теперь нажимать на поршень шприца, то жидкость выливается под действием давления поршня, которое передаётся в жидкости по закону Паскаля.
3. Опыт Торричелли. Измерение атмосферного давления.
Как провести опыт Торричелли? Возьмём стеклянную трубку длиной 1 м, у которого один конец запаян, и заполним ртутью. Зажмём открытый конец трубки с ртутью пальцем, перевернём её и опустим в чашку с ртутью. Под ртутью в чашке уберём палец. Часть ртути из трубки вытечет в чашку, а в трубке останется столб ртути высотой 76 см. Почему не вся ртуть из трубки вытекла?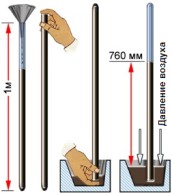
Над ртутью в трубке нет воздуха (образовалась пустота - вакуум), а на ртуть в чашке давит атмосфера. Вес столба ртути уравновесил атмосферное давление. Давление ртутного столба 76 см равно атмосферному давлению.
Задача 2. Вычислите атмосферное давление по давлению столба ртути 76 см.
Дано: СИ Решение.
h = 76 см 0,76 м pрт.ст. = g·ρ·h; ратм = pрт.ст;
ρ = 13 600 кг/м3 ратм = 9,8 Н/кг ·13 600 кг/м3·0,76 м = 101 292,8 Па ≈
g = 9,8 Н/кг ≈ 101 300 Па ≈ 101,3 кПа.
ратм - ? Ответ. ратм = 101,3 кПа.
Запомни среднее атмосферное давление: ратм = 100 кПа = 760 мм рт.ст.
Атмосферное давление в разную погоду немного меняется, при этом столбик ртути поднимается или опускается в пределах 740 - 770мм рт.ст.
Прибор для измерения атмосферного давления называется барометром.
Так как водяной пар легче воздуха (пар поднимается кверху!), то влажный воздух легче сухого. Поэтому перед грозой обычно атмосферное давление понижается: говорят, барометр падает (стрелка отклоняется влево).
При ясной погоде сухой воздух тяжелее, поэтому атмосферное давление увеличивается.
В физике принято считать нормальными условиями атмосферное давление ро = 101,3 кПа = 760 мм рт.ст. и температуру to = 0С
Задача 3. Какой высоты водяной столб уравновесит атмосферное давление?
Дано: Решение.
ро = 100 кПа
ρ = 1 000 кг/м3
g = 10 Н/кг
h - ? Ответ. h = 10 м.
Дома. 1. Ответьте на вопросы: а) Что такое атмосфера? б) Как объяснить атмосферное давление у поверхности Земли? в) Почему ртутный столбик в опыте Торричелли высотой около 76 см? г) Чему равно нормальное атмосферное давление в кПа и в мм рт.ст.? д) Что такое нормальные условия?
2. Вычислите массу m[кг] и вес Р[Н] воздуха в комнате размерами 3 м х 5 м х 12м.
3. Решите качественные задачи.
а) Почему при поднятии поршня в шприце набирается жидкость?
б) Атмосферное давление уравновешивает столб воды высотой 10 м. А какой высоты понадобился бы столб жидкости плотностью в 2 раза больше?
в) В солнечное безоблачное утро барометр показывал 760 мм рт.ст. К вечеру обещали дождь. Каким могло стать атмосферное давление: 750 мм рт.ст., 765 мм рт.ст. или 770 мм рт.ст.?
4. Расскажите с помощью таблицы опыт Торричелли.
5. На оценку "5" по желанию прочитайте на стр.99 а) задание 3 про автопоилку для птиц и б) задание 4 про прибор ливер для взятия проб жидкостей.
Тема 34. Задачи на атмосферное давление. §41, 44
1. Зависимость атмосферного давления от высоты над Землёй.
Чем выше, тем атмосфера всё более разрежена. Если на уровне океана атмосферное давление 100 кПа или 760 мм рт.ст., то на высоте Эльбруса около 5,5 км - в 2 раза меньше, т.е. около 50 кПа или 380 мм рт.ст. Если подняться ещё выше на 5,5 км, т.е. до 11 км, то атмосферное давление понижается ещё в 2 раза и будет около 25 кПа или 190 мм рт.ст.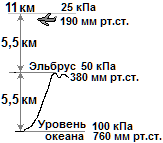
Задание на уроке. 1. Вычислите атмосферное давление на высоте 16,5 км (в кПа и в мм рт.ст.), если на уровне океана оно было нормальным.
На высоте 300 км, где летают космические станции, атмосфера настолько разрежена, что практически не мешает полёту. Отдельные молекулы земной атмосферы есть и на высоте 1 000 км, а дальше начинается безвоздушное пространство. Точную верхнюю границу атмосферы Земли нельзя определить.
Для небольших высот менее 1 км зависимость атмосферного давления можно рассчитывать так: на каждые 12 м вверх атмосферное давление понижается на 1 мм рт.ст. Рассмотрим две задачи с решениями.
Задача 1. Если у подножья горы нормальное давление 760 мм рт.ст., то какое давление будет на вершине горы высотой 480 м?
Решение. 1) 480 м : 12 = 20 мм рт.ст. - на столько давление меньше;
2) на вершине давление будет 760 мм рт.ст. - 20 мм рт.ст. = 740 мм рт. ст.
Задача 2. На земле барометр показал 756 мм рт.ст., а наверху телевизионной мачты 736 мм рт.ст. Какова высота мачты?
Решение. 1) 756 мм рт.ст. - 736 мм рт.ст. = 20 мм рт.ст.
2) 12 м∙20 = 240 м - высота мачты.
Задание на уроке. 2. Оформите решения двух противоположных задач.
а) На вершине горы атм.давление 740 мм рт.ст., а у подножья горы нормальное давление 760 мм рт.ст. Вычислите высоту горы.
б) Наверху телевизионной башни Омска барометр показал 736 мм рт.ст. Что покажет барометр на земле, если высота башни 240 м?
2. Качественные задачи на атмосферное давление.
Вопрос 1. Земля притягивает молекулы воздуха. Почему они не падают вниз?
- Потому что притяжение между молекулами воздуха слабое, а летают они с большими скоростями (больше 0,5 км/с - как пули). Поэтому при ударах друг об друга молекулы воздуха отскакивают.
Вопрос 2. Но если скорость молекул воздуха большая, то почему они не улетают в космос?
- Оказывается, чтобы покинуть Землю, нужна вторая космическая скорость 11,2 км/с, а скорость молекул воздуха намного меньше (не больше 1 км/с).
Вопрос 3. Почему внизу на земле плотность атмосферы больше, чем вверху?
- Потому что верхние слои атмосферы давят на нижние слои.
Задача 3. Можно ли качать воду очень мощным насосом из реки на берег высотой 20 м? Где надо расположить насос?
Решение. Если насос будет вверху ,на берегу, всасывать воду из реки, то вода поднимется по трубе не выше 10 м, т.к. воду загоняет по трубе вверх атмосферное давление, которое равно давлению столба воды всего 10 м. Если насос расположить внизу, под берегом, то он будет нагнетать воду вверх на любую высоту, на которую хватит мощности насоса.
Дома. 1. Разберитесь, как изменяется атмосферное давление при поднятии на высоту 5,5 км, 11 км, 16,5 км.
2. На оценку "3" решите две задачи на изменение атм.давления на 1 мм рт.ст. при изменении высоты на 12 м.
а) На вершине Эйфелевой башни барометр показал 735 мм рт.ст., а на земле 760 мм рт.ст. Вычислите высоту Эйфелевой башни.
б) На вершине горы высотой 480 м атмосферное давление 740 мм рт.ст. Найдите атмосферное давление у подножья горы.
3. Воздушный шар объёмом 50 л наполнен углекислым газом плотностью 2 кг/м3. Найти массу шара (в граммах) и силу тяжести на шар, не считая оболочку.
4. Решите устно две качественные задачи.
а) Где больше атмосферное давление: на чердаке дома или в подвале?
б) Насос стоит на высоте 9 м от воды. Можно ли закачать воду в бак на 2 м?
Тема 35. Барометр-анероид. §42, 43
1. Устройство и принцип работы барометра-анероида.
Ртутный барометр для измерения атмосферного давления в быту опасен для жизни, т.к. ртуть и его испарения ядовиты. Поэтому используют металлический барометр-анероид (анероид в переводе с греческого - безжидкостный).
О сложных приборах на уроке физики надо отвечать по такому плану:
1) Для чего предназначен прибор?
Барометр-анероид предназначен для измерения атмосферного давления, особенно он нужен метеорологам для предсказания погоды.
2) Из каких основных частей состоит прибор?
Барометр-анероид состоит из гофрированной (волнистой) металлической коробки, закреплённой между пластинами стальной пружины. Из коробки выкачан воздух. Коробка через передающий механизм соединена со стрелкой-указателем, который показывает давление на шкале.
3) Как работает прибор (как возвращается в обратное положение)?
При увеличении атмосферного давления гофрированная коробка сжимается. Стальная пружина тоже сжимается и через нить поворачивает стрелку прибора вправо - прибор показывает увеличение давления.
Когда давление понижается, коробка расширяется - нить ослабляется. Тогда возвратная пружинка поворачивает стрелку влево - в сторону уменьшения давления.
Атмосферное давление принято измерять в гектопаскалях: 1гПа = 100 Па. Нормальное атм. давление 101,3 кПа = 1 013 гПа = 760 мм рт.ст.
Полезно помнить: 750 мм рт.ст. = 1 000 гПа.
На барометре кроме стрелки-указателя есть стрелка-фиксатор, чтобы "запомнить" прошлое показание. На рисунке стрелка-фиксатор показывает 766 ± 0,5 мм рт.ст. или 1 022 0,5 гПа.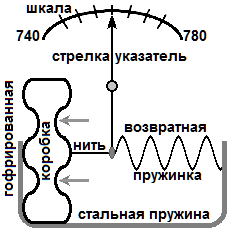
Задание на уроке. 1. Запишите показание стрелки-указателя барометра.
2. Из равенства 750 мм рт.ст. = 1 000 гПа с помощью пропорции превратите в гектопаскали 780 мм рт.ст. Ответ. 1 040 гПа.
2. Знаменитые опыты на атмосферное давление.
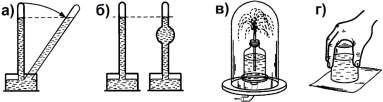
а) Если трубку в опыте Торричелли наклонить, то по закону о сообщающихся сосудах высота уровня ртути от поверхности ртути в стакане будет та же!
б) Высота ртути в трубке Торричелли от формы трубки не зависит.
в) Сосуд с водой плотно закрыли пробкой, через которую проходит трубочка. Над водой есть воздух. Если этот сосуд поместить под воздушный колокол и начать высасывать из-под колокола воздух, образуется фонтан. Дело в том, что давление воздуха над водой в сосуде будет больше, чем давление воздуха над водой в трубке.
г) Стакан с водой закройте листком бумаги, прижмите ладонью и переверните. Уберите ладонь - вода не выльется! Давление воздуха в стакане будет меньше атмосферного, т.к. бумага слегка прогнётся, поэтому атмосферное давление будет удерживать вес воды на лист бумаги. (Учитель показывает опыт!)
Задание на уроке. 2. Прочитайте на стр.103 из Упражнения 19 задание 2 про Магдебургские полушария Отто Герике.
3. С какой силой давит столб атмосферы на стол площадью 1 м2? По формуле F = p∙S = 100 000 Па∙1м2 = 100 000 Н - это вес груза 10 тонн! Почему же крышка стола не ломается? Потому, что атмосфера давит снизу с такой же силой, и эти две силы компенсируются.
Дома. 1. Выполните устно из Упражнения 19 на стр.103-104 задания 1, 3 и все 5(а, б, в, г).
2. Выполните практически Задания 11 на стр.104 (все: 1, 2 и 3).
3. Решите письменно задачу 4 из Упражнения 21 на стр.107.
Тема 36. Манометр. Поршневой жидкостный насос. §45, 46
1. Манометры. Поршневой жидкостный насос.
Задание на уроке. 1. Посмотрите опыты с жидкостным манометром, которые покажет учитель (как на стр.108, рис 126 и 127). Попробуйте их объяснить.
2. Прочитайте на стр.109 рис.128 и 129, как работает металлический манометр. Изучите его работу также по плакату.
3. По плакату и тексту §46 на стр.130 разберитесь, как работает поршневой жидкостный насос.
4. Расскажите про манометр и поршневой насос по таблице и плакатам:
Название и
назначение
прибора
Устройство
прибора
Принцип
работы
прибора
Металлическ- ий манометр
предназначен для измерения давления газа или жидкости.
Главные части - полая железная трубка в виде дуги, соединённая через передающий механизм со стрелкой-указателем.
Манометр подключают к сосуду с газом (жидкостью) под давлением. Газ (жидкость) наполняет трубку и немного выпрямляет дугу, которая через передающий механизм поворачивает стрелку вправо (больше). При уменьшении давления дуга сгибается обратно, и спиральная пружина возвращает стрелку назад.
Поршневой
жидкостный
насос служит для выкачивания жидкости из колодца или глубокого бака.
Главные части - цилиндр, поршень с рукояткой и два клапана: всасывающий и нагнетательный.
При поднятии рукоятки вверх верхний нагнетательный клапан закрыт. Вода с помощью поршня поднимается вверх и выливается через кран. Под поршнем образуется вакуум. Вода под действием атмосферного давления поднимается по трубе и заполняет цилиндр.
При опускании рукоятки вода течёт через нагнетательный клапан вверх, а всасывающий клапан закрыт под давлением поршня.
(Учащиеся устно отвечают по плакату на доске)
2. Гидравлический пресс.
Задание на уроке. 2. По чертежу разберите решение задачи. Сообщающиеся сосуды площадью S1 = 16 м2 и S2 = 32 м2 заполнены водой и накрыты подвижными поршнями, на которых лежат грузы F1 = 400 Н и F2 = 800 Н. Докажите, что грузы находятся в равновесии.
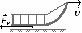 Гидравлический пресс представляет собой два сообщающихся цилиндра, накрытых поршнями разных площадей S1 и S2.
Гидравлический пресс представляет собой два сообщающихся цилиндра, накрытых поршнями разных площадей S1 и S2.
Если пресс находится в равновесии, то давление в сообщающихся сосуда по закону Паскаля должно быть одинаково: р1 = р2. По определению давления получаем:
 . Правые части равны:
. Правые части равны: 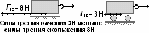
Соберём одинаковые буквы вместе: 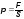
Правило равновесия гидравлического пресса:
силы, действующие на поршни, прямо
пропорциональны площадям поршней.
По-другому правило гидравлического пресса можно сформулировать так:
Чем больше площадь поршня, тем больше сила, действующая на поршень
(если поршни находятся в равновесии)
Задание на уроке. 3. Прочитайте на стр.112-113 о применении гидравлического пресса для выигрыша в силе. Разберитесь, как работает пресс.
Объясните работу всасывающего клапана 6 и нагнетательного клапана 7:
а) при опускании рукоятки и б) при поднятии рукоятки.
Для чего нужен предохранительный клапан 5?
Дома. 1. Приготовьтесь в классе рассказывать по плану (назначение, устройство и принцип работы) а) барометра-анероида; б) металлического манометра; в) поршневого насоса; г) гидравлического пресса. На доске будут висеть плакаты этих устройств.
2. С какой силой давит столб атмосферы на корочку учебника физики площадью 3,5 дм2?
3. По готовому рисунку суметь вывести формулу гидравлического пресса. Выучить правило в рамочке.
Тема 36 (Продолжение). Домкрат. Решение задач на давление. §47
1. Устройство и работа домкрата.
Гидравлический домкрат предназначен для поднятия тяжёлых грузов вручную. Главные части: цилиндр малой площади шток, на которую действует рука человека, и цилиндр большой площади плунжер, поднимающий груз.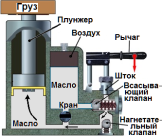
При нажатии на рычаг шток опускается: всасывающий клапан закрыт пружинкой, нагнетательный клапан открыт под давлением масла (пружинка сжата). Масло под давлением поднимает плунжер.
При поднятии рычага шток поднимается вверх: нагнетательный клапан закрывается пружинкой. Под штоком образуется вакуум. Атмосфера в воздушной камере давит на масло, и масло поднимается вслед за штоком.
Чтобы опустить груз, поворачивают кран и масло из-под плунжера свободно перетекает в резервуар с воздухом.
Задание на уроке. 1. Разберитесь, как работает автомобильный тормоз (стр.114, Задание 13, рис.135).
Задача на домкрат. На малый поршень (шток) домкрата площадью 2 см2 человек давит рукой с силой 200 Н. Какой вес может поднять большой поршень (плунжер) площадью 80 см2? Какой получим выигрыш в силе?
Дано: Решение.
S1 = 2 см2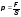
F1 = 200 H
S2 = 80 см2 Выигрыш в силе: F2: F1 = 8 000 Н : 200 Н = 40 раз.
F2 - ? Ответ. F2 = 8 кН; в 40 раз.
Задание на уроке. 2. Решите задачу про домкрат.
На шток площадью 1,5 см2 давит человек весом 800 Н и поднимает на плунжере автомобиль весом 16 кН. Найдите площадь плунжера и выразите в квадратных дециметрах.
2. Подготовка к контрольной работе №2. Задачи на давление.
1. Качественные задачи.
а) Почему взрыв снаряда под водой губителен для живущих под водой живых организмов? Какой закон физики надо использовать?
б) Почему не выливается вода из опрокинутой вверх дном полной бутылки, если её горлышко погружено в воду?
в) Почему мяч, вынесенный из комнаты на улицу зимой, становится слабо надутым? По какому закону физики?
г) Надувной матрац заполнен воздухом. Одинаковое ли давление будет в матраце, когда человек на нём лежит и когда стоит?
д) Электрические лампы наполняют газом, давление которого значительно меньше атмосферного. Почему так поступают?
е) В два одинаковых сосуда налиты вода и керосин. Оказалось, что силы давления жидкостей на дно сосудов одинаковы. Возможно ли это?
ж) На одном из уроков физики ученик утверждал, что показания барометра за окном комнаты должны быть больше, чем в комнате, поскольку на улице на него действует значительно больший столб атмосферного воздуха. Прав ли ученик?
з) Почему удобнее наливать сок из тетрапака, если пробить в крышке ещё одно отверстие?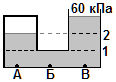
и) В сообщающихся сосудах на рисунке левое колено закрыто, а правое открыто. В точке В давление на дне сосуда составляет 60 кПа. Какое будет давление жидкости в точках А и В? На уровне 1? На уровне 2 в правом колене?
Решение. По закону Паскаля на одном и том же уровне на дне сосуда давление одинаково, значит, в точках А, Б и В давление по 60 кПа. На уровне 1 давление во всех трёх частях на третью часть меньше, т.е. 40 кПа, на уровне 2 в правом колене давление в 3 раза меньше - 20 кПа.
2. Вычислительные задачи.
а) Когда объём цилиндра уменьшили от 20 см3 до 12 см3, то давление газа увеличилось до 120 кПа. Найти начальное давление газа р1 в цилиндре.
б) Какова высота водонапорной башни, если манометр показывает давление столба воды 50 кПа? Плотность воды следует помнить.
в) Какое давление покажет барометр на дне шахты глубиной 240 м, если на поверхности земли было нормальное атм.давление 760 мм рт.ст.?
г) Какова масса воздуха в комнате длиной 5 м, шириной 4 м и высотой 3 м, если плотность воздуха 1,3 кг/м3? Найти вес этого воздуха. (Два ответа!)
д) С какой силой давит атмосфера на крышку стола размерами 8 дмХ15 дм, если атмосферное давление равно 100 кПа? Ответ дать в кН.
е) В домкрате на шток площадью 2 см2 давит тяжестью всего тела человек массой 60 кг. Какой вес Р2 может он поднять на плунжере площадью 40 см2?
Внимание! В классе разобрать только формулы для решения задач.
Дома. 1. Оформить решения задач а) - е), которые не успели сделать в классе.
Ответы ко всем задачам среди чисел: 5; 12; 72; 78; 120; 780.
Тема 37. Выталкивающая сила. §48, 49
1. 1. Вывод формулы выталкивающей силы FА.
Купаясь в реке, легко убедиться, что под водой любое тело легче, чем это же тело над водой. Почему? Потому что под водой на тело действует выталкивающая сила против силы тяжести и стремится поднять тело вверх. За счёт чего возникает выталкивающая сила? Оказывается, за счёт разности давления жидкости на разной глубине.
 На меньшей глубине h1 на верхнюю грань тела действует меньшее давление р1 = g ρж·h1, а на глубине h2 действует большее давление р2 = g ρж·h2. Значит и сила давления F1 на верхнюю грань будет меньше, чем сила F2 на нижнюю грань. Равнодействующая двух сил F1 и F2 равна разности сил FА = F2 - F1 и направлена в сторону большей силы F2, то есть направлена вверх. Эту силу FА называют выталкивающей силой или силой Архимеда.
На меньшей глубине h1 на верхнюю грань тела действует меньшее давление р1 = g ρж·h1, а на глубине h2 действует большее давление р2 = g ρж·h2. Значит и сила давления F1 на верхнюю грань будет меньше, чем сила F2 на нижнюю грань. Равнодействующая двух сил F1 и F2 равна разности сил FА = F2 - F1 и направлена в сторону большей силы F2, то есть направлена вверх. Эту силу FА называют выталкивающей силой или силой Архимеда.
Вывод формулы силы Архимеда. Из определения давления р = F/S выразим силу: F = p·S, поэтому F1 = p1·S = g ρж·h1·S и F2 = p2·S = g ρж·h2·S (площади верхнего и нижнего основания одинаковы S). Отсюда сила Архимеда:
FА = F2 - F1 = g ρж·h2·S - g ρж·h1·S = g ρж·S (h2 - h1) = g ρж·S h = g ρжVт, так как h2 - h1 = h - это высота тела, а произведение h·S = Vт - это объём тела.
Формула силы Архимеда или выталкивающей силы: FА = g ρжVт.
Архимедова сила приложена к телу, погружённому в жидкость (или газ). Эта сила направлена вверх против силы тяжести и выталкивает тело из жидкости.
Запомни! FА[Н] - выталкивающая сила (сила Архимеда); g = 10 Н/кг;
ж [кг/м3] - плотность жидкости; VТ [м3] - объём тела.
2. Качественные задачи на силу Архимеда.
По формуле FА = g ρжVт видно:
а) выталкивающая сила прямо пропорциональна плотности жидкости ρж;
б) выталкивающая сила прямо пропорциональна объёму тела Vт.
Задача 1. На рычажных весах уравновесили два одинаковых стальных шарика. Левый шар погрузили в воду, а правый шар - в бензин. Как изменится равновесие весов?
 Решение. Объёмы тел одинаковы, значит, выталкивающие силы зависят только от плотности жидкости. Но плотность воды ρв больше плотности бензина ρб, значит выталкивающая сила в воде больше. Поэтому шар в воде поднимется, а в бензине опустится.
Решение. Объёмы тел одинаковы, значит, выталкивающие силы зависят только от плотности жидкости. Но плотность воды ρв больше плотности бензина ρб, значит выталкивающая сила в воде больше. Поэтому шар в воде поднимется, а в бензине опустится.
Задача 2. На рычажных весах уравновесили два стальных шара разных по объёму: у шара слева объём больше. Потом оба шара погрузили в воду. Как изменится равновесие шаров?
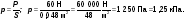 Решение. Плотность жидкости одинакова, значит, архимедовы силы зависят только от объёмов тел. Так как объём левого шара больше, то на него действует и большая архимедова сила. Поэтому левый шар поднимется, а правый опустится.
Решение. Плотность жидкости одинакова, значит, архимедовы силы зависят только от объёмов тел. Так как объём левого шара больше, то на него действует и большая архимедова сила. Поэтому левый шар поднимется, а правый опустится.
3. Вычислительные задачи на силу Архимеда.
Для решения задач надо повторить превращения единиц объёма в СИ.
1 м3
1 дм3 или 1 л
1 см3 или 1 мл
Запятая на 3 цифры
0,001 м3
0,000 001 м3
Задание на уроке. 1. Преобразуйте единицы объёма в СИ.
а) 450 дм3 = … м3; б) 20 дм3 = … м3; в) 3 000 л = … м3; г) 5 л = … м3;
д) 1 500 дм3 = … м3; е) 25 000 см3 = … м3; ж) 250 мл = … м3; з) 0,5 дм3 = … м3.
Задача 3. Человек объёмом 80 дм3нырнул под воду. Какая выталкивающая сила действует на него?
Дано: СИ Решение.
V = 80 дм3 0,08 м3FА = g ρвVт;
ρв = 1 000 кг/м3FА = 10 Н/кг·1 000 кг/м3·0,08 м3 = 800 Н.
g = 10 Н/кг
FА - ? Ответ. FА = 800 Н.
Задание на уроке. 2. Вычислите выталкивающую силу:
а) на насос объёмом 1,5 дм3, погружённый в керосин плотностью 0,8 кг/дм3;
б) на тело человека объёмом 80 дм3 в воздухе плотностью 1,3 кг/м3.
Дома. 1. На оценку "3" выучите опр. архимедовой силы в рамочке, формулу, объяснение всех величин в формуле (См. Запомните!) и решения Задач 1-3.
2. На оценку "4" и "5" знать вывод формулы силы Архимеда.
3. Решите письменно качественные задачи а) и б) и вычислительную в).
а) Два медных шара 2 дм3 и 3 дм3 уравновесили на весах, а потом погрузили оба шара в воду. Какой из шаров поднимется на весах? Почему?
б) В Задаче 1 (см. верхний рисунок) левый шар погрузили в керосин, а правый - в бензин. Что случится с шаром, помещённым в бензин?
в) Найти FА, действующую на камень объёмом 45 дм3, погружённый в керосин.
Тема 38. Закон Архимеда. §49
1. Каков физический смысл формулы силы Архимеда?
Обратите внимание, что в формуле силы Архимеда FА = g ρжVт произведение ρжVт - это масса жидкости в объёме тела, или по-другому говоря, масса жидкости, вытесненная телом: mж = ρж·Vт. Тогда формулу силы Архимеда можно переписать короче: FА = g·mж. Но по такой формуле находят вес жидкости. Отсюда получаем физический смысл выталкивающей силы:
Выталкивающая сила FА равна весу жидкости, вытесненной телом.
Этот вывод можно проверить на опыте с ведёрком Архимеда. Подвесим пустое ведёрко и груз к динамометру: пусть их вес будет 3Н. Опустим груз в сосуд с отливной трубкой, наполненный водой до самой трубки. Тогда из сосуда выльется в стакан столько воды, каков объём тела. На тело в воде будет действовать выталкивающая сила, поэтому динамометр покажет вес 2Н.
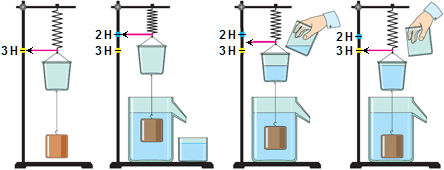
Выльем воду из стакана в ведёрко: динамометр снова покажет 3Н. Значит, вес вытесненной воды равен выталкивающей силе!
2. Закон Архимеда.
Теперь перейдём к закону Архимеда. Возьмём тело массой m. Его вес в воздухе Р = m·g. Погрузим тело полностью в жидкость, тогда вес тела в жидкости будет Р1, меньше на архимедову силу: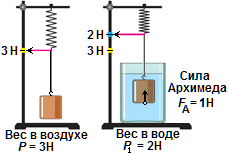
P1 = Р - FA - это и есть формула закона Архимеда, где Р1 - вес тела в жидкости, Р - вес тела в воздухе и FА - выталкивающая архимедова сила.
Отсюда FА = Р - Р1 = 3Н - 2Н = 1Н.
Закон Архимеда. Тело, погружённое в жидкость, теряет в весе столько, сколько весит жидкость, вытесненная телом.
Формулу закона Архимеда можно записать многими способами. В общую формулу Р1 = Р - FА можно подставить Р = mg, тогда получим: Р1 = mg - FА.
Если подставить FА = gжVт, то получим Р1 = Р - gжVт. Наконец, если подставить оба выражения, получим: Р1 = m·g - g ρжVт.
Теперь массу тела m выразим через плотность вещества тела: m = ρт·Vт и подставим снова в формулу закона Архимеда: Р1 = ρт·Vтg - g ρжVт. Вынесем одинаковые множители за скобки: Р1 = g·(ρт - ρж)·Vт.
2. Расчётные задачи на закон Архимеда.
Задача 1. Динамометр с подвешенной гирькой показывает 4 Н. После опускания гирьки в керосин динамометр стал показывать 3,2 Н. С какой силой керосин выталкивает гирьку?
Дано:
Решение.
Р = 4 Н
Р1 = 3,2 Н
По закону Архимеда Р1 = Р - FА, откуда FА = Р - Р1;
FА = 4 Н - 3,2 Н = 0,8 Н.
Ответ. FА = 0,8 Н.
FА - ?
Задача 2. Гирька массой 600 г погружена в жидкость, которая действует на гирьку с выталкивающей силой 4,2 Н. Найти вес гирьки в жидкости.
Дано: СИ Решение.
m = 600 г 0,6 кг Р1 = Р - FА, где Р = m·g. Отсюда получим
FА = 4,2 Н расчётную формулу: P1 = m·g - FA.
g = 10 Н/кг P1 = 0,6 кг·10 Н/кг·- 4,2 Н = 6 Н - 4,2 Н = 1,8 Н.
Р1 - ? Ответ. P1 = 1,8 Н.
Задание на уроке. 1. Решите задачи на ф-лы: Р1 = Р - gжVт и Р1 = m·g - g ρжVт.
а) Батискаф весом 20 кН объёмом 1,5 м3 опустили в воду. Каков вес батискафа в воде?
б) Тело массой 800 г объёмом 200 дм3 опустили в керосин плотностью 800 кг/м3. Найдите вес тела под керосином.
Задача 3. Сколько весит в воде стеклянный шар объёмом 200 см3?
Дано: СИ Решение.
V = 200 см3 0,0002 м3Р1 = g·(ρст - ρв)·V;
ρст = 2 500 кг/м3 Р1 = 10 Н/кг·(2 500 кг/м3 - 1 000 кг/м3)· 0,0002 м3 =
ρв = 1 000 кг/м3 = 1 500·0,002 Н = 3 Н.
g = 10 Н/кг
Р1 - ? Ответ. P1 = 3 Н.
Задача 4. Объём твёрдого тела, тяжелее воды, легко найти опытным путём. Например, вес тела в воздухе 1,2 Н, а под водой 0,8 Н. Надо найти объём тела.
Дано: Решение.
Р =1,2 Н P1 = Р - FA, где FА = g ρвVт; отсюда P1 = Р - g ρвVт;
Р1 = 0,8 Н перенесём слагаемые: g ρвVт = Р - P1, отсюда
ρв = 1 000 кг/м3
g = 10 Н/кг 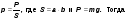
Vт - ? Ответ. Vт = 40 см3.
Дома. 1. На оценку "3" выучите правило и закон Архимеда в рамочках. Решите хотя бы первые две задачи.
а) На батискаф весом 20 кПа под водой действует выталкивающая сила 15 кПа. Найти вес батискафа под водой.
б) На гирьку массой 800 г под водой действует выталкивающая сила 6,4 Н. Найти вес гирьки под водой.
в) Блок весом 200 Н и объёмом 20 дм3 опустили в керосин плотностью 0,8 дм3. Найдите вес блока в керосине.
г) Сколько весит в керосине стеклянный шар объёмом 100 см3, если плотность стекла 2,5 г/см3, плотность керосина 0,8 г/см3?
Тема 39. Решение задач на закон Архимеда. §49
1. Качественные задачи на закон Архимеда.
1. Три одинаковых размера шарика из меди, цинка и стекла погрузили в воду.
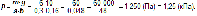 а) Одинаковая ли выталкивающая сила действует на эти тела? Объясните решение, используя формулу силы Архимеда.
а) Одинаковая ли выталкивающая сила действует на эти тела? Объясните решение, используя формулу силы Архимеда.
б) С одинаковой ли силой натянуты нити, на которых подвешены тела? Объясните по формуле закона Архимеда.
Решение. а) Так как объёмы тел одинаковы и плотность жидкости одинакова, то по формуле FА = gжVт выталкивающие силы одинаковы. б) Натяжение нити равно весу тела в воде Р1. По формуле Р1 = Р - FА видно, что чем больше вес в воздухе Р, тем сильнее натянута нить. Т.к. Р = mg, где m = ρт·Vт, то вес Р зависит от плотности ρт. По таблице на стр.50 плотность меди 8 900 кг/м3 наибольшая, а стекла 2 500 кг/м3 наименьшая, значит, наибольшее натяжение нити у медного шарика, а наименьшее - у стеклянного.
2. На рычажных весах уравновесили два одинаковых алюминиевых тела. Левое тело погрузили в машинное масло, а правое тело - в эфир. Как изменится равновесие весов?
3. На рычажных весах уравновесили два тела: на левом плече - из свинца, на правом - из алюминия. Оба тела опустили в бензин. Как изменится равновесие весов?
4. Одинаковую ли силу придется приложить, чтобы удержать на весу пустое ведро или то же ведро, наполненное водой и целиком находящееся в воде?
5. Почему держаться на поверхности воды в море значительно легче, чем в реке?
6. Ведро, доверху наполненное водой, висит на крюке динамометра. В ведро опускают кусок железа, подвешенный на нити. Изменится ли показание динамометра? А если бы ведро было налито наполовину?
Решение. Из доверху наполненного ведра выльется часть воды, и высота столба воды останется прежним, поэтому показание динамометра не изменится. В неполном ведре высота столба воды повысится, поэтому давление на дно ведра увеличится, а показание динамометра увеличится.
2. Вычислительные задачи на закон Архимеда.
1. Определите объём куска алюминия (в кубических дециметрах), на которую под водой действует выталкивающая сила 540 Н.
2. Лёгкую закрытую пластиковую бутылку объёмом 2,5 л удерживают погружённой в жидкость плотностью 0,8 кг/дм3. Какую силу при этом приходится приложить, чтобы бутылка не всплыла?
3. Какая выталкивающая сила действует в керосине на чугунный брусок размерами 50 см Х 20 см Х 10 см?
4. Сколько весит бетонная плита объёмом 0,2 м3 в воздухе? Сколько весит эта же плита в воде?
5. Какая выталкивающая сила действует в воде на железный брусок массой 780 г? Найдите вес этого бруска под водой.
6. Мраморная плитка в воздухе весит 27 Н, а под водой 17 Н. Найдите объём этой плитки и её массу.
Дома. 1. Прочитайте на стр.183-184 §8. Легенда об Архимеде.
2. Уметь записывать формулу закона Архимеда различными способами.
Тема 40. Условие плавания тел. §50
1. Тело тонет, тело плавает, тело всплывает и плавает наверху.
Если тело находится полностью в жидкости, не касаясь дна сосуда, то на него всегда действуют две силы: вниз сила тяжести Fтж и вверх выталкивающая сила FA. При этом возможны три случая.
а) Если плотность вещества тела больше плотности жидкости (железный шар в воде), то сила тяжести Fтж > FA., тогда тело тонет.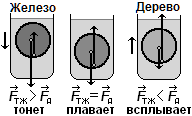
б) Если плотности тела и жидкости одинаковы, то Fтж = FA, тогда тело плавает внутри воды, не поднимаясь и не опускаясь.
в) Если плотность тела меньше плотности жидкости (деревянный шар под водой), тогда Fтж < FA, и тело всплывает до тех пор, пока выталкивающая сила не станет равной силе тяжести. Часть тела поднимается над водой до тех пор, пока снова станет Fтж = FA и тогда тело плавает уже на поверхности воды.
2. Условие плавания тел.
Опустим тело в сосуд с отливной трубкой. В стакан выльется такой объём воды, каков объём подводной части тела. Это означает, что вес всего тела равен весу воды, вытесненной подводной частью тела!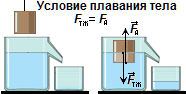
Если тело свободно плавает, то погружённая в жидкость часть тела вытесняет столько жидкости, сколько весит всё тело целиком
По-другому: тело плавает, если вес тела (сила тяжести) равен выталкивающей силе: Fтж = FА .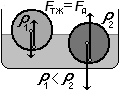
Чем плотность тела больше плотности жидкости, тем больше тело погружено в жидкость. Например, дубовый шар плотностью ρ2 = 700 кг/м3 больше погружается в воду, чем сосновый шар плотностью ρ1 = 400 кг/м3. Оба шара плавают на поверхности воды, так как их плотности меньше плотности воды ρв = 1 000 кг/м3.
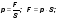 Если в сосуд налить две несмешивающиеся жидкости различной плотности, то более плотная жидкость расположится внизу, а менее плотная жидкость сверху.
Если в сосуд налить две несмешивающиеся жидкости различной плотности, то более плотная жидкость расположится внизу, а менее плотная жидкость сверху.
Например, машинное масло легче воды (плотность меньше), поэтому масло будет сверху, а вода снизу.
3. Качественные задачи на плавание тел.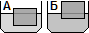
1. Одно и то же тело плавает в спирте А и в сероуглероде Б.
Ответы запишите цифрами: 1) А; 2) Б; 3) одинаково.
а) В каком сосуде Fтж больше? б) В каком сосуде FА больше?
в) В каком сосуде объём вытесненной телом жидкости больше?
г) Где вес вытесненной жидкости больше? д) Где плотность жидкости больше?
Решение. а) Т.к. тела одинаковы, то и Fтж одинаковы. б) Т.к. тела плавают, то Fтж = FA, но Fтж одинаковы, значит, и FA одинаковы. в) В спирте А тело глубже. г) Т.к. FA одинаковы, то и вес вытесненной жидкости одинаков. д) Т.к. сероуглерода Б вытеснено меньше, то его плотность больше. Ответ: 3, 3, 1, 3, 2.
2. На каком из рисунков тело 1 - тонет, 2 - всплывает, 3 - плавает свободно?
Сравнивайте векторы Fтж и FА. Ответ в виде 6-значного числа.
3. Шарики из каких металлов плавают в ртути: 1) железо, 2) медь, 3) золото, 4) платина, 5) олово, 6) осмий? Ответ в виде 3-значного числа.
4. Неполную бочку с водой поставили на весы и а) пустили в бочку живую рыбу; б) положили в воду деревянный брусок; в) человек опустил в воду руку. В каких случаях изменились показания весов и как именно?
5. Поплавок со свинцовым грузилом опускают один раз а) в воду, другой раз б) в масло. Известно, что в одном из случаев поплавок тонет. В каком?
6. В стакан налили воду, бензин и ртуть. Эти жидкости не смешивающиеся. Покажите на рисунке и подпишите, как расположатся жидкости.
7. На поверхности воды плавают бруски из дерева, пробки и льда. Укажите, под каким номером брусок из пробки и под каким номером брусок изо льда.![]()
Дома. 1. Проделайте опыт с яйцом и картофелиной (см.стр.123 задание 3).
2. Прочитайте на стр.122 из §50 про водных животных. Ответьте на последние три вопроса 5, 6 и 7 в конце параграфа.
Тема 41. Плавание судов. Задачи на плавание тел. §51
1. Плавание судов.
Чтобы понять, почему тяжёлое стальное судно плавает, проведём опыт. Алюминиевую фольгу (обёртку от шоколада) скомкаем и бросим в воду. Т.к. алюминий в 2,7 раза тяжелее воды, то комок фольги тонет в воде. Но если из этой фольги сделать кораблик, то он плавает.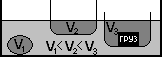
Причина в том, что комок фольги очень мал по объёму V1 и вытесняет мало воды, поэтому выталкивающая сила мала. А кораблик своим дном вытесняет такой объём воды V2 по весу, сколько весит вся фольга, из которой изготовлен кораблик. А если в кораблик положить ещё и груз, то кораблик осядет глубже и вытеснит ещё больше воды V3. Тогда выталкивающая сила станет больше и уравновесит вес кораблика с грузом.
Корабль с грузом плавает потому, что вес корабля с грузом равен весу воды, вытесненной подводной частью корабля. По-другому: вес корабля с грузом P уравновешивается выталкивающей силой воды FА.
Осадкой судна называется глубина h [H], на которое погружено в данный момент судно.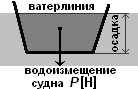
Ватерлинией наз. наибольшая допустимая осадка, которая обозначена на корпусе судна красной линией.
Водоизмещением судна наз. наибольший допустимый вес Р судна с грузом при погружении до ватерлинии.
Например, если вес самого судна 200 кН, а его водоизмещение 700 кН, то это судно может поднять на борт наибольший груз весом 700 кН - 200 кН = 500 кН.
Водоизмещение = вес судна + вес груза.
2. Решение задач на плавание тел.
Задача 1. Деревянный плот объёмом 0,4 м3 плавает в воде, погрузившись ровно наполовину. Найдите выталкивающую силу, действующую на плот. Какой максимальный груз может держать плот?
Решение. FА = gжVт, где Vт - это половина объёма плота 0,2 м3 и плотность воды ж = 1 000 кг/м3. Отсюда выталкивающая сила FА = 10Н/кг∙1 000 кг/м3∙0,2 м3 =
= 2 000 Н = 2 кН. Плот может поднять наибольший груз Р, пока не погрузится в воду вторая половина плота, т.е. ещё Р = 2 кН.
Задача 2. Тело весом 6 кН плавает в воде, погрузившись ровно наполовину. Найдите объём этого тела.
Дано:
СИ
Решение.
Р = 6 кН
ж = 1 000 кг/м3
g = 10 Н/кг
6 000 Н
FА = gжVт, где Vт - это половина объёма тела;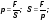
V = 2∙VТ = 2∙0,6 м3 = 1,2 м3.
Ответ. V = 1,2 м3.
V - ?
Задача 3. Судно водоизмещением 1 200 кН может поднять максимально 900 кН груза. Каков вес самого судна?
Решение. Водоизмещение = вес судна + вес груза; 1 200 кН = вес судна + 900 кН, откуда вес судна = 1 200 кН - 900 кН = 300 кН.
Задача 4. Яхта, погружённая в воду до ватерлинии, вытесняет 20 м3 воды. Вес самой яхты 140 кН. Чему равен вес груза?
Решение. Водоизмещение яхты равно выталкивающей силе: FА = gжVт,
FА = 10 Н/кг∙1 000 кг/м3∙20 м3 = 200 000 Н = 200 кН.
Вес груза = водоизмещение - вес яхты = 200 кН - 140 кН = 60 кН.
Задача 5. Какой объём бревна массой 200 кг погружён в воду?
Дано:
Решение.
m = 200 кг
ж= 1 000 кг/м3
g = 10 Н/кг
По условию плавания Fтж = FA, mg = gжVт.
Сократим обе части на g, получим m = жVт, откуда
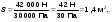
Ответ. VТ = 0,2 м3.
VT - ?
Задача 6. Кусок льда плавает в стакане. Что будет с уровнем воды в стакане, когда лёд растает?
Решение. Если лёд растает, то его масса не изменится, а значит, и выталкивающая сила не изменится. Уровень не изменится.
Дома. 1. Выучить правило в рамочке и определения понятий осадка, ватерлиния, водоизмещение. Знать словесную формулу водоизмещения.
2. Найдите вес груза, которое несёт судно водоизмещением 1 200 кН, если вес судна составляет 400 кН.
3. Яхта, погружённая в воду до ватерлинии, вытесняет 120 м3 воды и несёт при этом груз 800 кН. Найдите вес самой яхты?
4. Какой объём воды вытесняет подводная часть лодки массой 120 кг?
Тема 42. Воздухоплавание. §52
1. Воздухоплавание.
На любое тело, помещённое в воздухе, тоже действует выталкивающая сила, как и в воде. Но эта сила в сотни раз меньше, чем в воде, поэтому мы её часто не замечаем. Но если плотность газа внутри шара меньше, чем плотность воздуха вокруг шара, то вес шара будет меньше выталкивающей силы воздуха. Тогда шар под действием выталкивающей силы будет подниматься вверх и даже может поднять какой-то груз.
Какие же газы имеют плотность меньше, чем плотность воздуха? Прежде всего, это горячий воздух, которым наполняли первые воздушные шары. Ещё есть лишь два газа легче воздуха - это водород Н2 и гелий Не.
Задание на уроке. 1. Изучите расчёт выталкивающей силы водорода и гелия на стр.127 из §52. Какой газ легче и у какого газа выталкивающая сила больше?
Какие летательные аппараты применяются в воздухоплавании? Воздушные шары (по-другому аэростаты) не имеют приспособлений для управления полётом и летят по ветру. Но на них можно регулировать высоту полёта. Для перевозки пассажиров и грузов раньше применялись управляемые дирижабли. Для подъёма на большие высоты для научных целей применялись стратостаты. В настоящее время для изучения погоды регулярно запускают небольшие метеорологические зонды. К дирижаблям и стратостатам для размещения людей и груза подвешиваются гондолы. У стратостата гондола герметичная.
Задание на уроке. 2. Прочитайте §52 и решите качественную задачу. Обозначим 1) аэростат, 2) дирижабль, 3) зонд, 4) стратостат. Ответьте на вопросы и ответ запишите в виде 6-значного числа (например, 233 141):
а) Можно наполнять горячим воздухом. б) Гондола прочная и герметичная.
в) Вместо гондолы ящик с приборами. г) Служил для перевозки людей и грузов.
д) Чтобы подняться, с них сбрасывали балласт. е) Имел гондолу с двигателем.
2. Подготовка к Контрольной работе №3. Закон Архимеда.
Качественные задачи на выталкивающую силу и закон Архимеда.
1. (Трудная задача) На воде плавает льдинка со алюминиевым шариком внутри. Как изменится уровень воды, когда весь лёд растает?
Решение. Пусть льдинка весила 30 Н и шарик 3 Н. Тогда льдинка с шариком вытеснили 33 Н воды. Когда льдинка растаяла, то шарик упадёт на дно. Пусть шарик давит на дно с силой 2Н, а вытесняет воду лишь на 1 Н. Значит, уровень воды уменьшится на 2 Н (вместо 33 Н останется 31 Н).
2. Почему стальной корабль плавает, а стальной гвоздь тонет?
Решение. Потому что корабль подводной частью вытесняет такой вес воды, сколько весит корабль. А гвоздь вытесняет воды меньше, чем сам весит.
3. Как изменится осадка корабля при переходе из реки в море?
Решение. Т.к. плотность морской солёной воды больше (1 003 кг/м3), чем пресной речной воды (1 000 кг/м3), то корабль должен вытеснить в море меньший объём солёной воды. Осадка корабля в море уменьшится.
4. В банку с ртутью уронили железный гвоздь. Что с ним произойдёт?
Решение. Гвоздь будет плавать на поверхности ртути, т.к. плотность железа меньше плотности ртути.
5. В неполный сосуд с водой опустили одинаковые по размерам и форме бруски: один раз деревянный, другой раз железный. Как изменится уровень воды?
Решение. Деревянный брусок будет плавать и погрузится лишь частично, а железный утонет и погрузится полностью. Значит, деревянный брусок вытеснит меньше воды, и уровень воды поднимется меньше.
Количественные задачи на выталкивающую силу и закон Архимеда.
Повторите формулы: а) Сила Архимеда: FА = gжVт, где g = 10 Н/кг; ж [кг/м3] - плотность жидкости; VТ [м3] - объём тела.
б) Закон Архимеда: Р1 = Р - FА, где Р1 - вес тела в жидкости, Р = mg - вес тела в воздухе. Отсюда Р1 = m·g - g ρжVт или Р1 = g·(ρт - ρж)·V.
1. (Повторите из Темы 37 задачу 3 и решите следующую задачу).
Мина объёмом 150 л плавает под водой. Вычислите выталкивающую силу, действующую на мину. Устно: каков вес мины в воздухе и вес мины в воде.
2. (Повторите из Темы 38 задачу 1 и решите следующую задачу).
Пластилиновый шарик весом 1,2 Н, погружённый в керосин, оказался легче на 0,9 Н, чем в воздухе. Вычислите вес шарика в керосине. Как изменился бы вес этого шарика, если бы его погрузили под воду?
3. (Повторите из Темы 38 задачу 2 и решите следующую задачу).
Шар массой 120 г подвесили к динамометру и погрузили в воду. В воде на шар действует сила Архимеда 0,9 Н. Найти показание динамометра.
4. (Повторите из Темы 38 задачу 3 и решите задачу, пользуясь таблицей на с.51).
Найти вес алюминиевого шара объёмом 200 дм3, погружённого в керосин.
5. (Повторите из Тему 41 задачу 5).
Деревянный плот своей подводной частью вытесняет 1,2 м3 воды. Вес плота в воздухе 8 кН. Какой наибольший груз может удержать плот?
Дома. 1. Для подготовки к Контрольной работе №3 надо уметь решать любые из пяти качественных и из пяти количественных задач.
2. Дополнительное Задание 16 на стр. 125-126. Разберитесь, как работает прибор ареометр для измерения плотности жидкостей.
3. На стр.128 из Упражнения 27 разберите задания 1 и 2 по рис.147 и 148.
Тема 43. Механическая работа. §53
1. Что такое механическая работа.
Рассмотрим задачу. Мальчик тащит по дороге санки. Выясним, от чего зависит механическая работа, которую выполняет мальчик над санками. Ясно, что чем санки тяжелее, тем больше силы должен приложить мальчик, а значит, и больше работы он совершит.
Механическая работа А прямо пропорциональна силе F.
Ясно также, чем больший путь ![]() пройдёт мальчик с санками, тем больше механической работы А он совершит.
пройдёт мальчик с санками, тем больше механической работы А он совершит.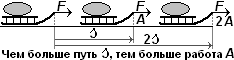
Механическая работа А прямо пропорциональна пути ![]() . Но если работа А пропорционально силе F и пропорциональна пути
. Но если работа А пропорционально силе F и пропорциональна пути ![]() , то работа пропорциональна произведению F ·
, то работа пропорциональна произведению F · ![]() . В системе СИ коэффициент пропорциональности принимают за единицу 1, поэтому получаем формулу работы: A = F ·
. В системе СИ коэффициент пропорциональности принимают за единицу 1, поэтому получаем формулу работы: A = F · ![]() .
.
Опр. Механической работой А наз. произведение силы F на путь ![]() , если сила направлена в ту же сторону, куда перемещается тело.
, если сила направлена в ту же сторону, куда перемещается тело.
В системе СИ сила F измеряется в ньютонах [H], путь ![]() - в метрах [м], тогда механическая работа А измеряется в джоулях [Дж] в честь английского учёного Джеймса Джоуля: 1 Дж = 1 Н · 1 м.
- в метрах [м], тогда механическая работа А измеряется в джоулях [Дж] в честь английского учёного Джеймса Джоуля: 1 Дж = 1 Н · 1 м.
2. Три простейшие задачи на формулу механической работы.
Задача 1. На летящий снаряд действовала сила трения воздуха 0,05 кН. Снаряд пролетел 1,2 км и упал. Найти работу силы трения воздуха.
Дано: СИ Решение.
F = 0,05 кН 50 Н A = F · ![]() ;
;
![]() = 1,2 км 1 200 м A = 50 Н · 1 200 м = 60 000 Н = 60 кН.
= 1,2 км 1 200 м A = 50 Н · 1 200 м = 60 000 Н = 60 кН.
А - ? Ответ. A = 60 кН.
Задача 2. Под действием силы тяги 2,5 кН автомобиль совершил механическую работу 0,4 МДж. Какой путь прошёл автомобиль за это время?
Дано: Решение.![]()
F = 2,5 кН 2 500 Н A = F · ![]() ;
;
А = 0,4 МДж 400 000 Дж ![]()
![]() - ? Ответ.
- ? Ответ. ![]() = 160 м.
= 160 м.
Задача 3. Пуля проникла вглубь ствола дерева на 8 см. При этом силы трения совершили над пулей 3,2 кДж работы. Найти среднюю силу трения.
Дано: СИ Решение.![]()
![]() = 8 см 0,08 м A = F ·
= 8 см 0,08 м A = F · ![]() ;
;
А = 3,2 кДж 3 200 Дж ![]()
F -? Ответ. F = 40 кН.
3. Решение задач на формулу механической работы A = F · 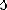 .
.
Решите в классе задачи, сходные с задачами 1, 2 и 3.
1. Штангист поднял штангу весом 2 кН на высоту 1м 80 см. Какую механическую работу совершил штангист? Ответ. А = 3,6 кДж.
2. Какой путь прошёл мотоцикл, если под действием тяги мотора 0,8 кН было совершено 40 кДж механической работы? Ответ. ![]() = 50 м.
= 50 м.
3. От удара молотка гвоздь вошёл в дерево на глубину 5 см, при этом молоток совершил 0,08 кДж работы. Какова средняя сила трения гвоздя о дерево?
Ответ. F = 1,6 кН.
Если нужно найти механическую работу по поднятию тела массой m на высоту h, то сила F равна силе тяжести F = m∙g. Тогда работа А = F∙h = mg∙h. Эту формулу работы полезно помнить! Решите задачу по этой формуле.
4. Какую работу надо совершить, чтобы достать из колодца глубиной 5 м ведро воды массой 12 кг? Ответ. А = 600 Дж.
Качественные задачи на механическую работу.
1. Какая сила совершает работу? Найдите по таблице соответствия и запишите ответ в виде 6-значного числа.
А) яблоко с ветки падает на землю
1) сила упругости газа
2) сила упругости пружины
3) сила тяжести
4) сила трения
5) сила мышц
6) сила Архимеда
Б) штангист поднимает вверх штангу
В) воздушный шар поднимается вверх
Г) снаряд движется в стволе пушки
Д) шайба катится по льду, пока не остановится
Е) сжатая пружина толкнула шарик
2. Бочка заполнена водой. Пользуясь ведром, половину воды из бочки вычерпала девочка, оставшуюся половину - мальчик. Одинаковую ли работу они совершили?
3. Нужно переложить одинаковые книги с нижней полки на верхнюю. Одинаковая ли работа будет совершена при перекладывании:
а) целиком пачки 1) в пачку А) на верхнюю полку и
б) пачки 2) по одной книге на полку В)?
Дома. 1. Выучите определение в рамочке, формулу работы и все три буквы в формуле (в чём измеряются и какую физическую величину обозначают).
2. Решите следующие 3 задачи (письменно в тетради).
а) Под действием силы тяги 3,5 кН автомобиль совершил механическую работу 0,5 МДж. Какой путь прошёл автомобиль за это время?
б) Какую работу совершил мальчик массой 48 кг, поднявшись по лестнице на высоту 15 м?
в) Пуля застряла в мешке с песком на глубине 1,5 дм. Найти среднюю силу трения пули о песок, если пуля совершила 0,6 кДж механической работы.
3. Какая сила совершает работу? Запишите ответ в виде 5-значного числа.
А) Футбольный мяч катится по полю и тормозит
1) сила двигателя
2) сила Архимеда
3) сила тяжести
4) сила трения
5) сила упругости
Б) Самолёт опускается над аэродромом
В) подводная лодка поднимается из глубины
Г) стрела летит под натяжением тетивы лука
Д) вертолёт взлетает вверх с аэродрома
Тема 43. Механическая работа (продолжение). §53
1. Когда механическая работа НЕ совершается.
а) Если на тело действует сила, но тело не перемещается, т.е. ![]() = 0 м., то и механическая работа А = 0. Например, спортсмен держит на вытянутых руках штангу. Как бы тяжело ему не было, но механическую работу он не совершает.
= 0 м., то и механическая работа А = 0. Например, спортсмен держит на вытянутых руках штангу. Как бы тяжело ему не было, но механическую работу он не совершает.
б) Если тело перемещается по инерции, то все силы, действующие на тело уравновешиваются (компенсируются), т.е. F = 0., но тогда и работа А = 0. Например, шайба, катящаяся по очень гладкому льду, работу не совершает.
в) Наконец, если сила направлена перпендикулярно перемещению тела, то эта сила работы не совершает. Например, на шайбу, скользящую по инерции, перпендикулярно вниз действует сила тяжести, но работы она не совершает. Как бы странно не было, но если человек несёт в руке чемодан или на плече мешок, то он механическую работу над этими телами не совершает!
г) Не совершается механическая работа при мыслительных процессах, например, при решении задачи "в уме". Но играя в мяч, ребёнок совершает механическую работу, т.к. под действием силы руки мяч приходит в движение. Таким образом, понятие "работа" в бытовом понятии не всегда совпадает с физическим понятием "механическая работа".
Задание на уроке. В каких случаях совершается механическая работа:
а) штангист поднимает штангу; б) человек печатает на клавиатуре;
в) человек держит на плече груз; г) человек несёт на плече тяжёлый груз;
д) мама на прогулке толкает равномерно детскую коляску;
е) вода давит на стенку сосуда; ж) мальчик влезает на дерево.
2. Задачи на механическую работу по расчётной формуле.
Задача 1. Мальчик в течение 30 с тащил санки со скоростью 2 м/с с силой 50 Н. Какую работу совершил мальчик?
Дано:
Решение.
t = 30 c
v = 2 м/c
F = 50 Н

Получим расчётную формулу: А = Fv t.
А = 50 Н∙2 м/с∙30 с = 3 000 Дж = 3 кДж.
Ответ. А = 3 кДж.
А - ?
Задача 2. Поршень площадью 2 дм2 под действием давления 0,8 кПа поднял груз на высоту 20см. Какую работу совершил поршень?
Дано:
СИ
Решение.
S = 20 дм2
р = 0,8 кПа
h = 20 см
0,2 м2
800 Па
0,2 м
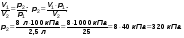
Получим расчётную формулу: A = pSh.
А = 800 кПа∙0,2 м2∙0,2 м = 32 Дж.
Ответ. А = 32 Дж.
А - ?
Задача 3. Вычислите работу при подъёме гранитной плиты объёмом 0,5 м3 на высоту 20 м. Плотность гранита 2 500 кг/м3.
Решение.
Дано: V = 0,5 м3; h = 20 м; ρ = 2 500 кг/м3; g = 10 Н/кг. Найти: А - ?
По формуле работы A = F · h, где сила тяжести F = m·g. Массу плиты выразим через плотность Тогда F = ρ·V·g, наконец A = ρ·V·g·h.![]()
A = 2 500 кг/м3·0,5 м3·10 Н/кг·20 м = 2 500 · 100 Н·кг = 250 000 Дж = 250 кДж.
Сравните решение Задачи 3 по действиям в учебнике на стр. 130-131.
Задание на уроке. С плотины высотой 25 м за секунду падает на лопасти турбины 120 м3 воды плотностью 1 000 кг/м3 и вращает турбину, совершая механическую работу. Вычислите эту механическую работу. Ответ. А = 30 МДж.
Дома. 1. Трактор в течение 10 мин тащил сани со скоростью 5 м/с с силой 10 кН. Какую работу совершил трактор?
2. Плунжер домкрата площадью 200 см2 под давлением 300 кПа поднял груз на высоту 2 см. Какую работу совершил плунжер? Ответ. А = 1,2 кДж.
3. В каких случаях НЕ совершается механическая работа? Ответ в виде числа.
1) Штангист держит штангу вверху. 2) Ученик несёт в руке портфель.
3) Хоккеист бьёт клюшкой по шайбе. 4) Шайба долго катится по гладкому льду.
5) Нефть в цистерне давит на дно. 6) Человек поднимается по лестнице.
Тема 44. Мощность. §54
1. Что такое мощность, в каких единицах измеряется?
Может ли человек выкопать такую же яму, как экскаватор? Может! Но только человек будет копать её очень долго. Дело в том, экскаватор за каждую минуту совершает работу во много раз больше, чем человек. Говорят, что экскаватор мощнее человека. Чтобы понять, что такое мощность, решим задачу.
Задача. Первый экскаватор выкопал яму объёмом 96 м3 за 8 час, а второй экскаватор выкопал яму 99 м3 за 9 час. Какой экскаватор мощнее?
Первый экскаватор за 1 час выкопает 96 м3: 8 = 12 м3;
второй экскаватор за 1 час выкопает 99 м3: 9 = 11 м3. Следовательно, первый экскаватор мощнее. Хотя он и совершил общий объём работы меньше, но за каждую секунду совершал больше работы.![]()
Чтобы найти мощность, надо работу делить на время:
Опр. Мощностью наз. отношение работы ко времени, за которое эта работа совершена.![]()
Формула мощности: , где мощность N измеряется в ваттах [Вт] в честь английского учёного Джеймса Уатта; работа А в джоулях [Дж] и время t в секундах [с]. Коротко так: N[Вт] - мощность; А[Дж] - мех работа; t[c] - время.
2. Три простые задачи на мощность.
Задача 1. На старте ракета за 1 минуту совершает работу 120 кДж. Найти мощность ракеты.
Дано:
СИ
Решение.
t = 1 мин
А = 120 кДж
60 с
120 000 Дж

Ответ. N = 2 кВт.
N - ?
Задача 2. Какую работу выполнит пылесос мощностью 0,6 кВт за 5 минут?
Дано:
СИ
Решение.
N = 0,6 кВт
t = 5 мин
600 Вт
300 с
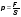
А = 600 Вт∙300 с = 180 000 Дж = 180 кДж.
Ответ. А = 180 кДж.
N - ?
Задача 3. За сколько времени кулер мощностью 1 200 мВт совершит работу 0,18 кДж?
Дано:
СИ
Решение.
N = 1 200 мВт
А = 0,18 кДж
7,2 Вт
600 Дж
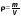
Ответ. t = 2,5 мин.
t - ?
Задание на уроке. Решите в классе задачи, сходные с задачами 1, 2 и 3.
1. Улитка совершила 2 400 мДж работы за 1 мин. Найти мощность улитки.
2. Мощность мотоблока 1,5 кВт. Какую работу совершит мотоблок при вспашке земли за 10 мин?
3. Насос мощностью 2,5 кВт выкачивает воду из колодца. Сколько времени должен работать насос, чтобы совершить 0,15 МДж работы?
3. Качественные задачи на мощность.
Задача 1. Ведро воды из колодца мальчик один раз достал за 20 с, а в другой раз за 30 с. Одинаковую ли работу совершил мальчик? одинакова ли мощность при выполнении этих работ?
Решение. Т.к. масса воды m и глубина колодца h одинаковы, то работу по формуле А = mgh мальчик выполнил одинаковую. Т.к. работа одинакова, а время 20 с в первом случае меньше, то по формуле мощности чем меньше время t, тем больше мощность N. Мощность обратно пропорциональна времени.
Задача 2. Папа с маленьким сыном за руку поднимаются на второй этаж. Одинаковую ли они совершили работу и одинаковая ли у них мощность?
Решение. Т.к. масса папы больше, то по формуле А = mgh папа совершил работы больше. Т.к. время подъёма t одинаково, но папа совершил больше работы A, то мощность папы больше. Мощность прямо пропорциональна работе.
Дома. Выучите опр. мощности в рамочке, формулу и все входящие величины.
Прочитайте по учебнику стр.134 из §54 и ответьте на вопросы:
а) Какова средняя мощность человека при нормальных условиях работы?
б) Какова наибольшая мощность человека? б) Какова мощность самолёта Ан-2?
Решите три задачи.
1. Найти мощность электродвигателя, совершившего 4,8 кДж работы за 10 мин.
2. Какую работу совершит электромотор мощностью 0,8 кВт за 2 мин?
3. За сколько времени кулер мощностью 1 200 мВт совершит работу 0,24 кДж?
Тема 44. Мощность (продолжение). §54
1. Задачи на расчётную формулу.
Задача 1. Какую среднюю мощность должен развить мальчик, чтобы достать из колодца глубиной 5 м ведро весом 120 Н за время 30 с?
Дано:
Решение.
h = 5 м
Р = 120 Н
t = 30 c
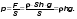
Ответ. N = 20 Вт.
N - ?
Задание на уроке. Решите самостоятельно задачу по расчётной формуле.
Какова средняя мощность мальчика массой 40 кг, если он за 2 мин забирается на дерево высотой 6 м? Ответ. N = 20 Вт.
Задача 2. Найти мощность транспортёра, который может поднять 5 м3 гравия плотностью 1800 кг/м3 на высоту 6 м за 10 мин.
Дано:
Решение.
V = 5 м3
= 1 800 кг/м3
h = 6 м
t = 600 с
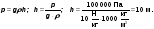
Ответ. N = 900 Вт.
N - ?
Внимание! В громоздких задачах в Дано: единицы измерения разрешается сразу записывать в системе СИ. В данной задаче вместо 10 мин сразу 600 с. Если все единицы измерения в СИ, то в расчётной формуле можно единицы измерения не писать. Но тогда в результате единицу измерения принято писать в скобках: 900 (Вт). Но в ответе скобки не нужны!
Задача 3. Петя может забежать на пятый этаж (n = 4) за полминуты. Высота одного этажа 3 м. Масса Пети 40 кг. Какую мощность развивает Петя?
Дано:
Решение.
n = 4
t = 30 с
h = 3 м
m = 40 кг
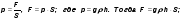
Ответ. N = 900 Вт.
N - ?
2. Задачи на нахождение буквы из расчётной формулы.
Задача 4. Мощность подъёмника 4 кВт. Какой груз он может поднять на высоту 15 м за 2 мин?
Дано:
Решение.
N = 400 Вт
h = 15 м
t = 120 с
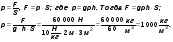
Ответ. Р = 3,2 кН.
Р - ?
Задание на уроке. Решите две задачи по расчётной формуле.
Задача 5. На какую высоту успеет поднять кран мощностью 10 кВт груз весом 5 кН за время 30 с? Ответ. h = 60 м.
Задача 6. Сколько времени должен работать насос мощностью 50 кВт, чтобы из шахты глубиной 150 м откачать воду объёмом 200 м3? Ответ. t = 1 ч 40 мин.
Дома. Решите три задачи (на оценку "3" хотя бы одну верно).
№1. Какую мощность развивает подъёмный кран, поднимая на высоту 12 м за 1 мин сразу 4 поддона кирпича (n = 4) весом по 5 кН каждый?
№2. За сколько времени кран мощностью 10 кВт поднимет груз весом 5 кН на высоту 6 м? Ответ. t = 30 с.
№3. Подъёмный кран мощностью 2,5 кВт поднимает балку массой 200 кг в течение 12 с. На какую высоту поднимет кран балку? Ответ. h = 15 м.
Дополнительная задача.
№4. Автомобиль движется со скоростью 72 км/ч и преодолевает сопротивление 0,8 кН. Найти мощность двигателя. (Выведите формулу N = Fv).
Тема 45. Простой механизм рычаг. §56
1.Что такое рычаг?
Чтобы удобнее и легче было работать, люди еще в древности изобрели множество простых механизмов. Изучим подробно простой механизм рычаг. Когда нужно поднять или сдвинуть слишком тяжёлый предмет, применяют длинную прочную палку - рычаг. Педаль тормоза автомобиля тоже представляет собой рычаг.
Опр. Рычагом называется твёрдое тело, которое может вращаться вокруг неподвижной опоры.
Самый простой рычаг первого рода представляет собой стержень, посередине которого находится точка опоры О. По обе стороны от точки опоры находятся плечи рычага ℓ1 и ℓ2, на которые действуют силы F1 и F2. Эти силы можно подобрать так, чтобы они уравновешивали друг друга, тогда рычаг будет в равновесии (неподвижен). При этом на короткое плечо рычага надо действовать с большей силой, а на длинное плечо - с меньшей силой.
На рисунке плечо ℓ1 = 6 см в два раза больше, поэтому на него действует сила F1 = 10 Н в два раза меньше, чтобы этот рычаг был в равновесии!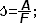
Во сколько раз плечо короче, во столько раз сила больше.
2. Условие равновесия рычага.
Рычаг находится в равновесии, если силы F1 и F2, действующие на него, обратно пропорциональны плечам рычага ℓ1 и ℓ2.
С обратной пропорциональностью вы встречались в законе Бойля-Мариотта (Тема 29), поэтому нетрудно составить формулу условия равновесия рычага: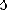

Задача 1. Короткое плечо рычага 40 см, длинное плечо 1 м 20 см. Вес человека 600 Н. Какой наибольший груз может приподнять человек своим весом при помощи этого рычага? Объясните, на какое плечо должен действовать человек.
Дано: СИ Решение.
ℓ1 = 40 см 0,4 м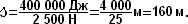
ℓ2 = 1 м 20 см 1,2 м
F2 = 600 Н
F1 - ? Ответ. F1 = 1,8 кН.
Эту задачу можно решить устно.
Т.к. длинное плечо в 120 см : 40 см = 3 раза больше короткого, то на короткое плечо должна действовать сила в 3 раза больше: 600 Н · 3 = 1 800 Н.
Из этой задачи видно, что если человек действует на длинное плечо, то рычаг даёт выигрыш в силе. В данной задаче сила 1 800 Н в 3 раза больше веса человека 600 Н, поэтому рычаг даёт выигрыш в силе в 3 раза.
Задача 2. На левом плече рычага 6 см висит груз 0,4 кН, а на правом плече груз 0,6 кН. Найти длину правого плеча, если грузы находятся в равновесии.
Дано:
Решение.
ℓ1 = 6 см
F1 = 0,4 кН
F2 = 0,6 кН
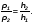
Ответ. ℓ2 = 4 см.
ℓ2 - ?
Задание на уроке. 1. Сделайте чертёж в масштабе (по клеткам) и решите задачу.
Меньшая сила, действующая на рычаг, равна 4 кН. Найти большую силу, если плечи рычага 6 дм и 3 дм. Объясните, на какое плечо действует меньшая сила.
2. Устно (с помощью чертежа) найдите силу или длину плеча:
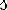
Дома. Выучите определение и правило в рамочках . Решите следующие задачи:
№1. На левом плече длиной 12 см висит груз весом 60 Н, а на правом плече груз весом 180 Н. Найти длину правого плеча, если грузы в равновесии.
№2. Человек несёт на плече груз весом 120 Н на конце рычага длиной 60 см. С какой силой он удерживает рукой другой конец рычага длиной 40 см?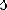
№3.Объясните, выигрыш или проигрыш в силе получает рука человека на данном рисунке. Что надо сделать, чтобы легче было нести груз на палке?
Тема 46. Момент силы. Рычаг второго рода. §57, 58.
1. Момент силы. Правило моментов.
К формуле условия равновесия рычага применим основное свойство пропорции (перемножить крест-накрест): F1·ℓ1 = F2·ℓ2.
Опр. Моментом силы М называется произведение силы F на плечо ℓ.
Момент силы М = F ·ℓ измеряется в [Н·м] - "ньютон·метрах".
Обозначим левую часть формулы равновесия рычага М1 = F1·ℓ1 и правую часть М2 = F2·ℓ2, тогда получим новую формулу условия равновесия рычага, которую называют правило моментов: М1= М2.
Правило моментов. Рычаг находится в равновесии, если момент силы на левом плече рычага равен моменту силы на правом плече.
Задача 1. На плечи рычага 60 см и 80 см подвесили грузы 12 Н и 9 Н соответственно. Будет ли этот рычаг находится в равновесии?
Решение.![]()
Момент силы на левом плече рычага:
М1 = F1·ℓ1 = 12 Н · 0,6 м = 7,2 Н·м;
Момент силы на правом плече рычага: М2 = F2·ℓ2 = 9Н · 0,8 Н·м = 7,2 Н·м.
Так как моменты сил равны М1= М2, то рычаг находится в равновесии.
Задание на уроке. 1. На левом плече 5 см висит груз 9 Н, а на правом плече 6 см висит груз 8 Н. Будет ли рычаг в равновесии? Какой груз перетянет?
Задание на уроке. 2. Прочитайте по учебнику стр.143 из §58 и ответьте на вопрос: Какие весы на рис.159 представляют собой равноплечий рычаг?
3. Решите устно Упражнение 30 (№2 и №3) на стр.144-145.
2. Рычаг второго рода. Как найти плечо силы рычага.
Мы изучили рычаги первого рода: у них плечи размещаются по разные стороны от точки опоры. А у рычага второго рода плечи размещаются по одну сторону от точки опоры.
Рычаг второго рода (на рис.) вращается вокруг точки опоры О. По середине рычага на короткое плечо ℓ1 = 0,4 м действует груз F1 = 10 Н вниз. А за конец длинного плеча ℓ2 = 0,8 м этот груз удерживают в равновесии с силой F2 = 5 Н вверх (например, рукой).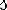
Обратите внимание, что плечо силы отсчитывается от точки опоры О до точки приложения силы.
Момент силы на коротком плече: М1 = F1·ℓ1 = 10 Н · 0,4 м = 4 Н·м и на длинном плече: М2 = F2·ℓ2 = 5Н · 0,8 Н·м = 4 Н·м. Так как моменты сил равны, то рычаг находится в равновесии.
3*. Как найти плечо силы рычага.
До сих пор мы рассматривали рычаги в виде прямого стержня, силы к которым приложены перпендикулярно. Но силы могут действовать и не перпендикулярно, а сами рычаги могут иметь любую форму.
На рис. вектор силы ![]() не перпендикулярен рычагу ОА. Чтобы найти плечо ℓ этой силы, надо:
не перпендикулярен рычагу ОА. Чтобы найти плечо ℓ этой силы, надо: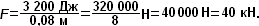
1) провести через вектор ![]() прямую АВ;
прямую АВ;
2) из точки опоры О опустить перпендикуляр ОВ на прямую АВ.
Тогда плечо силы будет ℓ = ОВ. Момент силы останется F∙ℓ.
Опр. Плечом силы наз. кратчайшее расстояние ℓ от точки опоры О до прямой, проведённой через вектор силы![]() .
.
Задание на уроке. 4. Разберитесь по рисункам, как надо измерять плечо силы ℓ.
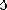
Дома. 1. Прочитайте на стр.160 Лабораторную работу №9. Приготовьтесь к выполнению этой работы на следующем уроке.
2. Из формулы равновесия рычага 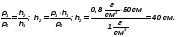 уметь вывести формулу М1 = М2. Выучить определение момента силы и правило моментов в рамочках.
уметь вывести формулу М1 = М2. Выучить определение момента силы и правило моментов в рамочках.
3. Пользуясь правилом моментов, устно определите, будут ли в равновесии рычаги на рисунках. Если рычаг не в равновесии, то какое плечо перевесит?
Тема 47. Ворот и блок. §59
1. Ворот - разновидность рычага первого рода.
Второй простой механизм - ворот применяется, например, у колодца или у ручной швейной машинки. Если внимательно посмотреть, то ворот - это рычаг первого рода.
Тяжёлое ведро с водой действует с силой F1 на короткое плечо ℓ1, равное радиусу ворота. А рука действует с меньшей силой F2 на более длинное плечо рычага ℓ2. Поэтому достать ведро с водой благодаря вороту легче!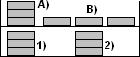
2. Неподвижный блок - разновидность рычага первого рода.
Наконец, третий простой механизм - блок бывает двух видов: подвижный блок и неподвижный блок. Неподвижный блок очень похож на ворот и представляет собой равноплечий рычаг первого рода. Неподвижный блок вращается вокруг оси О, которая неподвижно укреплена, и сам блок не перемещается. 
С помощью неподвижного блока можно поднимать вверх груз весом F1, если тянуть за верёвку вниз с силой F2. Так как плечи рычага равны ℓ1 = ℓ2, то и силы равны F1 = F2. Значит, неподвижный блок не даёт выигрыша в силе, а применяется для того, чтобы изменить направление движения.
3. Подвижный блок - разновидность рычага второго рода.
Подвижный блок представляет собой рычаг второго.
Один конец верёвки О неподвижно прикреплён к опоре - это и есть точка опоры. За другой конец верёвки в точке А тянут с силой F1вверх, действуя на плечо ℓ1. А груз весом F2 прикреплён к оси блока в точке В и вместе с блоком тоже поднимается вверх. Вес груза F2 действует на плечо ℓ2. Так как плечо ℓ1 в 2 раза больше плеча ℓ2, то сила F1 в 2 раза меньше веса груза F2. Значит, подвижный блок даёт выигрыш в силе в 2 раза. Если конец верёвки поднять вверх, например, на 1 метр, то груз поднимется вверх всего лишь на 0,5 метра. Зато поднимать груз с помощью подвижного блока в 2 раза легче, если не учитывать, конечно, вес самого блока и верёвок.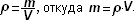
Вывод: ворот, неподвижный и подвижный блоки - это разновидности рычага.
Задача 1. Груз весом Р = 6 Н поднимают сразу с помощью двух блоков: неподвижного блока А и подвижного блока Б. С какой силой F надо тянуть за верёвку, чтобы равномерно поднимать груз?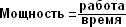
Решение. Подвижный блок Б даёт выигрыш в силе в 2 раза, поэтому вся верёвка будет натянута с силой F = Р:2 = 6 Н:2 = 3 Н.
Неподвижный блок А не даёт ни выигрыша, ни проигрыша в силе, поэтому верёвку надо тянуть с силой F = 3 Н.
Задание на уроке. 1. С помощью ворота радиусом ℓ1 = 20 см поднимают из колодца ведро с водой весом F1 = 120 Н. С какой силой F1надо крутить рукоятку с длиной рычага ℓ1 = 80 см, чтобы поднимать ведро. (Пользуйтесь верхним рисунком)
Задание на уроке. 2. На всех семи рисунках а)-ж) устно вычислите силу F. Не путайте рычаги первого рода на рис. а), б), д) и ж) с рычагами второго рода на остальных рисунках. Помните: плечо - это расстояние от точки О до силы F!
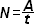
Дома. 1. Прочитайте на стр.145-147 весь §59 и ответьте на вопросы на стр.147.
2. Решите ещё раз все 7 задач на рисунке. Рассуждайте так: а) плечо силы F в 2 раза меньше плеча силы 10 Н. Значит, сила F в 2 раза больше, т.е. F = 20 Н.
3. Повторите определения и формулы из прошлой Темы 46 (Момент силы).
Решение задач на рычаги и блоки (дополнительно).
Задача 1. Сравните силы F1 и F2 на рисунках а) рычагов 1-ого и 2-ого рода;
б) неподвижного и подвижного блока:
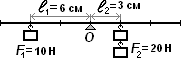
Задача 2. Решите более сложные задачи а) и б).
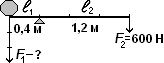
Задача 3. На левом плече рычага длиной 60 см висит груз массой 2,4 кг. С какой силой надо удерживать правое плечо длиной 40 см?
Дано: СИ Решение.
ℓ1 = 60 см 0,6 м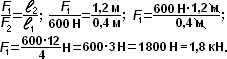
ℓ2 = 40 см 0,4 м
m = 2,4 кг
g = 10 Н/кг
F - ? Ответ. F1 = 36 Н.
Решите самостоятельно дома №4, №5 и №6.
№4. Два мальчика качаются на доске, лежащей на опоре. Миша весом 300 Н сидит на расстоянии 2 м от точки опоры. На каком расстоянии от точки опоры должен сесть Петя весом 500 Н, чтобы качели были в равновесии?
№5. Длина меньшего плеча 8 см и на нём висит груз 15 кг. С какой силой надо нажимать на короткое плечо 6 см, чтобы удержать равновесие?
№6. Один конец палки длиной 120 см лежит на опоре, а другой конец удерживают с силой 60 Н. На каком расстоянии от опоры подвешен груз массой 18 кг?
Задача 7. Папа массой 60 кг и сын массой 40 кг качаются на лёгком бревне длиной 5 м. На каком расстоянии от точки опоры должен сесть отец, чтобы качели были в равновесии.
Решение.
Пусть плечо рычага отца х, тогда плечо рычага сына 5 - х.
Вес отца Р1 = m·g = 60 кг·10 Н/кг = 600 Н, вес сына Р2 = 400 Н.
По правилу моментов сил получим уравнение:
Р1·х = Р2·(5 - х), 600·х = 400·(5 - х), 600·х = 2 000 - 400х, 600·х + 400х = 2 000, 1 000·х = 2 000, х = 2 м. Ответ. 2 м.
Решите самостоятельно дома №8, №9 и №10. За задачи №9 и №10 можно получить дополнительно оценку "5" в журнал. Решите на отдельном листке.
№8. На концах лёгкого стержня длиной 1м 60 см прикреплены два груза массами 300 г и 500 г. На каком расстоянии от меньшего груза нужно выбрать точку опоры, чтобы грузы оказались в равновесии.
№9*. К подвижному блоку массой 2 кг подвешен груз массой 20 кг. С какой наименьшей силой надо поднимать груз, если не учитывать трение? Найти работу этой силы для подъёма груза на высоту 5 м.
№10*. Решите задачу №4 из Упражнения 30 на стр.145. Отв. 7,2 кг.
Тема 48. "Золотое правило" механики. Наклонная плоскость.§60
1. Дают ли простые механизмы выигрыш в работе?
С помощью рычага можно как выиграть в силе, так и проиграть. Рычаг даёт выигрыш в силе, когда при поднимании тяжёлого груза мы действуем на длинное плечо. Но если действовать на короткое плечо рычага (см. весло лодки рис.161 на стр.145), то мы проигрываем в силе, зато выигрываем в пути: рука гребца совершает маленькое перемещение, а лодка совершает большое перемещение. Измерения на опыте показывают, что пути s1 и s2, пройденные концами рычага, обратно пропорциональны силам F1 и F2, на концах рычага.

Так как ворот является разновидностью рычага первого рода, то и ворот может дать как выигрыш в силе и при этом проигрыш в пути (ведро из колодца), так и наоборот, проигрыш в силе и выигрыш в пути (как швейная машинка). Но ворот никогда не даёт выигрыша в работе!
Неподвижный блок не даёт ни выигрыша, ни проигрыша в силе, и тем более не даёт выигрыша в работе: с его помощью мы лишь меняем направление силы.
А вот подвижный блок при отсутствии трения всегда даёт выигрыш в силе в 2 раза и соответственно проигрыш в пути в 2 раза, но выигрыша работеподвижный блок тоже не даёт. Ни один механизм не даёт выигрыша в работе!
"Золотое правило" механики:
Ни один простой механизм не даёт выигрыша в работе. Во сколько раз простой механизм даёт выигрыш в силе, во столько же раз даёт проигрыш в пути, и наоборот.
Задача 1. На подвижном блоке подняли груз 80 Н на высоту 2 м. Сколько метров верёвки надо перебрать и с какой силой? Найти механическую работу.
Решение. 1) Т.к. подвижный блок даёт проигрыш в пути в 2 раза, то верёвки надо перебрать h = 2·2 м = 4 м. Выигрыш в силе в 2 раза: F = 80 Н:2 = 40 Н.
2) Работа с помощью блока: А = F·h = 40 Н · 4 м = 160 Дж.
Без помощи блока работа такая же: А = Р·s = 80 Н · 2 м = 160 Дж.
Задача 2. Длинный конец рычага под действием силы 120 Н прошёл путь 60 см. На какой путь поднимет короткий конец рычага груз массой 30 кг?
Дано: СИ Решение.
F1 = 120 Н 1) Вес груза Р = m1·g = 30 кг · 10 Н/кг = 300 Н.
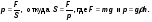 s1 = 60 см 0,6 м 2)
s1 = 60 см 0,6 м 2)
m1 = 30 кг
g = 10 Н/кг
s2 - ? Ответ. s2 = 0,24 м.
2. Наклонная плоскость, клин и винт. Простые механизмы. §55
Когда не хватает силы поднять тяжёлое бревно в кузов грузового автомобиля, применяют наклонную плоскость, которая даёт выигрыш в силе.
Пусть бревно весом Р = 800 Н надо поднять на высоту h = 1,5 м. Применим наклонную плоскость длиной s = 3 м, которая даст в 2 раза проигрыш в пути, а значит, в 2 раза выигрыш в силе. Мы можем закатить бревно с силой лишь F = 400 Н.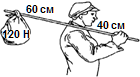
Но выигрыша в работе мы снова не получим:
1) работа по наклонной плоскости: А = F·s = 400 Н · 3 м = 1 200 Дж = 1,2 кДж;
2) без наклонной плоскости: А = Р·h = 800 Н · 1,5 м = 1 200 Дж = 1,2 кДж.
На наклонную плоскость похожи по принципу действия ещё два простых механизма - это клин и винт. Примером клина может служить топор или колун, которыми колют дрова. Примером винта может служить резьба, с помощью которой закручивается гайка на болт.
Классификация простых механизмов.
1. Рычаг.
Рычаг 1-ого рода
Рычаг 2-ого рода
а) Ворот
б) Неподвижный блок
Подвижный блок
2. Наклонная плоскость
Клин
Винт
Задание на уроке. Прочитайте §55 на стр.136-137 Простые механизмы и ответьте на вопросы в конце параграфов.
3. Задачи на "золотое правило" механики.
№1. Строитель поднимал на крышу здания ведро с цементом с помощью подвижного блока. Он перебрал руками 8 м верёвки с силой 90 Н. а) Найти вес ведра с цементом. б) Какой путь прошло ведро? в) Какую работу совершил строитель? (Повторите Тема 47 пункт 3. Подвижный блок)
№2. В задаче №1 измените подвижный блок на неподвижный и ответьте на те же вопросы (устно). Запишите только ответы а), б) и в).
№3. Человек массой 60 кг сел на длинный конец рычага и поднял другим концом груз весом 300 Н вверх на 20 см. На какое расстояние опустился вниз длинный конец рычага? Ответ. На 30 см.
№4. Рабочему надо закатить вверх на платформу высотой 1,5 м бочку весом 2 кН. Для этого он использовал наклонную плоскость длиной 5 м. С какой силой ему пришлось бы катить бочку, если бы не было трения? Отв. 600 Н.
Решите в классе из №1-№4 сколько успеете, остальное дома.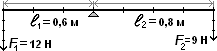
Дома. 1. На оценку "3" выучите "золотое правило" механики в рамочке и формулу из пункта 1: F1∙s1 = F2∙s2. Решите задачу №4 по формуле Р∙h = F∙s.
2. Выучите таблицу Классификация простых механизмов.
3. На оценку "4" и "5" надо уметь решать любые задачи из Темы 48.
Тема 49. Коэффициент полезного действия. §61.
1. Простые механизмы дают проигрыш в работе.
"Золотое правило" механики утверждает, что простой механизм не даёт выигрыша в работе. Об этом говорилось в прошлой теме в Задаче 1 про подвижный блок (см.стр. слева). Работа с помощью блока А = F∙h была 160 Дж и без блока А = Р·s тоже 160 Дж.
То же самое в задаче про наклонную плоскость: А = F·s = Р·h = 1,2 кДж. Но в этих задачах мы не учитывали вес самого блока и силу трения.
Работу, совершённую без применения механизмов, будем называть полезной работой Аполез, а с применением простых механизмов полной работой Аполн.
Ясно, что если учитывать вес самих простых механизмов и силу трения, то работа с помощью простых механизмов будет немного больше: Аполн > Аполез. Значит, простой механизм всегда приводит к проигрышу в работе!
Задание на уроке. Объясните на разных примерах, зачем пользуются простыми механизмами, несмотря на то что они дают проигрыш в работе.
2. Повторим задачи на проценты.
Процентом наз. сотая часть числа. Например, портной сшил вещь и продал её за цену ц = 100 руб. Своего труда он потратил часть ч = 20 руб.
Тогда ч = 20 руб. составляют от ц = 100 руб. двадцать сотых всей стоимости вещи: ч : ц = 20 руб.:100 руб. = 0,20, то есть 20%.
Чтобы найти, сколько процентов составляет часть ч от целого числа ц, надо часть делить на целое и умножить на 100%: 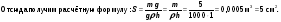
Приведём пример из физики. Чтобы поднять бревно с земли в кузов, надо совершить 160 Дж работы, а чтобы закатить её по наклонной плоскости надо затратить уже 200 Дж из-за трения. Какую часть в процентах составляет полезная работа 160 Дж от полной работы 200 Дж?
Для решения этой задачи надо полезную работу 160 Дж разделить на полную работу 200 Дж и умножить на 100%: 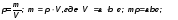
3. Коэффициент полезного действия простого механизма .
Коэффициентом полезного действия (КПД) простого механизма называется отношение полезной работы Аполез к полной работе Аполн.
КПД обозначается греческой буквой "эта" и измеряется десятичной дробью или в процентах: 0,6 = 60%.![]()
Так как полезная работа всегда меньше полной работы, то КПД простого механизма меньше 100%. Не существует в природе механизма с КПД = 100%, а тем более больше 100, например, 1,2 или 120%.
Подготовка к Лабораторной работе №10.
Измерим на опыте КПД наклонной плоскости. Действуем по алгоритму:
1) Установим наклонную плоскость на высоте h = 20 см = 0,2 м.
2) Измерим динамометром вес бруска с двумя гирьками Р = 2,4 Н.
3) Вычислим полезную работу по поднятию груза: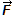
Аполез = Р∙h = 2,4 Н∙0,2 м = 0,48 Дж.
4) Измерим длину наклонной плоскости: s = 80 см = 0,8 м.
5) Будем тащить груз по наклонной плоскости и измерим силу F = 1 Н.
6) Вычислим полную работу на наклонной плоскости:
Аполн = F∙s = 1 Н∙0,8 м = 0,8 Дж.
7) Вычислим КПД наклонной плоскости:
![]()
Дома. 1. Выучите определение КПД в рамочке и формулу КПД.
2. Подготовьтесь к Лабораторной работе №10 по алгоритму из 7 шагов, а также прочитайте по учебнику стр.170-171.
Тема 50. Решение задач на КПД простых механизмов.
1. Задача на КПД наклонной плоскости.
Задача 1. По рисунку вычислите КПД наклонной плоскости.
Дано: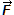
Решение.
Р = 2 000 Н
h = 1,5 м
s = 5 м
F = 800 Н
Аполез = Р·h = 2 000 Н · 1,5 м = 3 000 Дж.
Аполн = F·s = 800 Н · 5 м = 4 000 Дж.
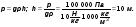
Ответ. = 50%.
- ?