- Учителю
- Методика организации научно-исследовательской деятельности школьников по небесной механике
Методика организации научно-исследовательской деятельности школьников по небесной механике
МОУ СОШ №4 г.Ростов Великий
</ Учитель физики Модулина Д.Г.
Методика организации научно - исследовательской деятельности школьников по небесной механике
Глава 1. Введение
Во многих развитых странах есть беспокойство, что ученики школы отворачиваются от науки. Для разрешения вопросов мотивации школьников к учению наиболее доступной выступает исследовательская деятельность. Под исследовательской деятельностью понимается процесс совместной деятельности учащегося и педагога по выявлению сущности изучаемых явлений и процессов, по открытию, систематизации новых знаний, поиску закономерностей, описанию, объяснению, проектированию.
Основной целью организации научно-исследовательской деятельности школьников по небесной механике является:
-
расширение представлений о практической применимости законов механики, углубление полученных знаний, их прикладного значения;
-
выявление и поддержка одарённых учащихся;
-
развитие их интеллектуальных и творческих способностей;
-
поддержка научно-исследовательских интересов учеников.
Задачи организации научно - исследовательской деятельности школьников по небесной механике:
-
Формирование представлений о познаваемости мира, единстве законов, объясняющих движение тел на Земле и в космосе;
-
Приобщение учащихся к интеллектуально - творческой деятельности;
-
Выдвижение и реализация в научных исследованиях творческих идей, создание научных работ и проектов;
-
Создание условий для расширения среды общения и получения информации;
-
Участие в проводимых в рамках района, края, страны научно - практических конференциях;
-
Формирование навыков исследовательской работы;
-
Развитие интеллектуальных, творческих и коммутативных способностей.
-
Овладение умениями применения дополнительных источников при изучении материала курса.
Глава 2. Основная часть
-
Исторический очерк.
Небесная механика принадлежит к числу древнейших наук. Уже в 6 в. до н. э. народы Древнего Востока обладали глубокими астрономическими знаниями, связанными с движением небесных тел. Но в течение многих веков это была только эмпирическая кинематика Солнечной системы. Основы современной небесной механики были заложены И. Ньютоном в «Математических началах натуральной философии» (1687). Закон тяготения Ньютона далеко не сразу получил всеобщее признание. Однако уже к середине 18 в. выяснилось, что он хорошо объясняет наиболее характерные особенности движения тел Солнечной системы. В работах Ж. Лагранжа и П. Лапласа были разработаны классические методы теории возмущений. Первая современная теория движения больших планет была построена У. Леверье в середине 19 в. Эта теория лежит до сих пор в основе французского национального астрономического ежегодника. В работах Леверье было впервые указано на необъяснимое законом Ньютона вековое смещение перигелия Меркурия, которое оказалось через 70 лет важнейшим наблюдательным подтверждением общей теории относительности.
Дальнейшее развитие теория больших планет получила в конце 19 в. в работах американских астрономов С. Ньюкома и Дж.Хилла (1895-1898). Работы Ньюкома открыли новый этап в развитии небесной механики. Он впервые обработал ряды наблюдений, охватывающие длительные интервалы времени и на этой основе получил систему астрономических постоянных, которая только незначительно отличается от системы, принятой в 70-х гг. 20 в. Чтобы согласовать теорию с наблюдаемым движением Меркурия, Ньюком решил прибегнуть к гипотезе А. Холла (1895), который для объяснения невязок в движении больших планет предложил изменить показатель степени в законе тяготения Ньютона. Ньюком принял показатель степени равным 2,000 000 161 20. Закон Холла сохранялся в астрономических ежегодниках до 1960, когда он был, наконец, заменен релятивистскими поправками, вытекающими из общей теории относительности. Продолжая традиции Ньюкома и Хилла, Бюро американских эфемерид (Вашингтонская морская обсерватория) под руководством Д. Брауэра и Дж. Клеменса в течение 40-х и 50-х гг. 20 в. осуществило обширные работы по переработке планетных теорий. В частности, в результате этой работы в 1951 были опубликованы «Координаты пяти внешних планет», что явилось важным шагом в исследовании орбит внешних планет. Эта работа была первым успешным применением электронных вычислительных машин в фундаментальной астрономической задаче. В СССР в 1964 была разработана аналитическая теория движения Плутона. Современная теория движения больших планет имеет настолько высокую точность, что путём сравнения теории с наблюдениями удалось подтвердить смещения планетных перигелиев, вытекающие из общей теории относительности, не только для Меркурия, но также для Венеры, Земли и Марса.
Первые теории движения Луны были разработаны А. Клеро, Ж. Д'Аламбером, Л.Эйлером и П. Лапласом. Наиболее совершенной с практической точки зрения была теория немецкого астронома П. Ганзена (1857), которая использовалась в астрономических ежегодниках с 1862 по 1922. В 1867 была опубликована аналитическая теория движения Луны, разработанная французским астрономом Ш. Делоне. Современная теория Луны основана на работах Дж. Хилла (1886). Построение таблиц Луны на основе метода Хилла было начато в 1888 американским астрономом Э. Брауном. В 1919 три тома таблиц вышли в свет и в астрономических ежегодниках на 1923 впервые была дана эфемерида Луны, основанная на таблицах Брауна. Для того чтобы согласовать теорию и наблюдения, Браун должен был (также как и Ганзен) ввести в разложения координат эмпирический член, который никак не объяснялся гравитационной теорией движения Луны. Только в 30-е гг. 20 в. окончательно выяснилось, что эмпирический член отражает эффект неравномерного вращения Земли в движении небесных тел. С 1970 эфемерида Луны в астрономических ежегодниках вычисляется непосредственно по тригонометрическим рядам Брауна без помощи таблиц.
Актуальное значение приобрела теория движения спутников больших планет, в первую очередь спутников Марса и Юпитера. Теория движения четырёх спутников Юпитера была разработана ещё Лапласом. В теории, предложенной В. де Ситтером (1919) и используемой в астрономических ежегодниках, учитываются сжатие Юпитера, солнечные возмущения и взаимные возмущения спутников. Внешние спутники Юпитера изучались в Институте теоретической астрономии АН СССР. Эфемериды этих спутников до 2000 года вычислены американским астрономом П. Хергетом (1968) с помощью численного интегрирования. Теория движения спутников Сатурна, основанная на классических методах, была построена немецким астрономом Г. Струве (1924-33). Устойчивость спутниковых систем рассмотрена в работах японского астронома Ю. Хагихара (1952). Советский математик М. Л. Лидов, анализируя эволюцию орбит искусственных спутников планет, получил интересные результаты и для естественных спутников. Им было впервые показано (1961), что, если бы орбита Луны имела наклон к плоскости эклиптики, равный 90°, то такая Луна уже после 55 оборотов, т. е. примерно через четыре года, упала на поверхность Земли. Наряду с разработкой теории высокой степени точности, но пригодной только: на сравнительно небольших интервалах: времени (сотни лет), в небесной механике ведутся также исследования движения тел Солнечной системы в космогонических масштабах времени, т. е. на протяжении сотен тысяч и миллионов лет. Попытки решить эту проблему долгое время не давали удовлетворительных результатов. Только появление быстродействующих вычислительных машин, произведших революцию в небесной механике, позволило снова вернуться к решению этой фундаментальной задачи. В СССР и за рубежом разработаны эффективные методы построения аналитической теории движения больших планет, открывающие возможность изучения движения планет на весьма длительных промежутках времени.
В связи с разработкой космогонической гипотезы О. Ю. Шмидта в 40-х гг. в СССР были выполнены многочисленные исследования финальных движений в задаче трёх тел; полученные в этих работах результаты имеют значение на неограниченном интервале времени. В США (1965) численным методом изучена эволюция орбит пяти внешних планет на интервале времени в 120 000 лет. Самым интересным результатом этой работы явилось открытие либрации Плутона относительно Нептуна, благодаря которой минимальное расстояние между этими планетами не может быть меньше 18 астрономических единиц, хотя в проекции на плоскость эклиптики орбиты Плутона и Нептуна пересекаются. В СССР выполнена обширная работа (1967) по применению теории вековых возмущений Лагранжа - Брауэра к изучению эволюции орбиты Земли на протяжении миллионов лет. Эта работа имеет важное значение для понимания изменения климата Земли в различные геологические эпохи.
Начало 20 в. было отмечено значительным прогрессом в разработке математических методов небесной механике. Этот прогресс был связан прежде всего с работами французского математика А.Пуанкаре, русского математика А. М. Ляпунова и финского астронома К. Сундмана. Последнему удалось решить общую задачу трёх тел с помощью бесконечных степенных сходящихся рядов. Однако ряды Сундмана оказались совершенно непригодными для практического использования из-за их крайне медленной сходимости. Сходимость рядов в небесной механике тесно связана с так называемой проблемой малых делителей. Математические трудности этой проблемы в значительной степени преодолены в работах математиков школы А. Н.Колмогорова.
Развитие небесной механики в СССР тесно связано с деятельностью двух научных центров, возникших непосредственно после Великой Октябрьской социалистической революции: теоретической астрономии института АН СССР в Ленинграде и кафедры небесной механики Московского университета. В этих двух центрах сложились ленинградская и московская школы, которые определили развитие небесной механики в СССР. В Ленинграде вопросы небесной механики разрабатывались главным образом в связи с такими практическими задачами, как составление астрономических ежегодников, вычисление эфемерид малых планет и др. В Москве доминирующее влияние на протяжении многих лет имели космогонические проблемы, а также астродинамика.
Среди иностранных научных учреждений, ведущих исследования в области небесной механики, видное место занимают: Вашингтонская морская обсерватория, Гринвичская астрономическая обсерватория, Бюро долгот в Париже, Астрономический институт в Гейдельберге и др.
-
Задачи, решаемые небесной механикой.
Небесная механика - раздел астрономии, изучающий движения тел Солнечной системы в гравитационном поле.
При решении некоторых задач небесной механики (например, в теории движения комет) учитываются также и негравитационные эффекты: реактивные силы, сопротивление среды, изменение массы. Важным разделом современной небесной механики является астродинамика, исследующая движения искусственных небесных тел. Методы, разрабатываемые небесной механикой, используются также при изучении и других небесных тел. Однако в современной астрономии такие вопросы, как изучение движении в системах двойных и кратных звёзд, статистические исследования закономерностей движения звёзд и галактик, относят к звёздной астрономии и внегалактической астрономии.
Задачи, решаемые небесной механикой, разделяются на четыре большие группы:
1. Разработка общих вопросов движения небесных тел в гравитационном поле (так называемая задача n тел, частными случаями которой являются задача трёх тел и задача двух тел).
2. Построение математических теорий движения конкретных небесных тел как естественных, так и искусственных (планет, спутников, комет, космических зондов).
3. Сравнение теоретических исследований с астрономическими наблюдениями и определение таким путём числовых значений фундаментальных астрономических постоянных (элементы орбит; массы планет; постоянные, связанные с вращением Земли, характеризующие фигуру Земли и её гравитационное поле, и др.).
4. Составление астрономических эфемерид, которые концентрируют в себе результаты теоретических исследований в области небесной механики и фиксируют на каждый момент времени фундаментальную пространственно-временную систему отсчёта, необходимую для всех разделов науки, имеющих дело с измерением пространства и времени.
-
Задача трёх тел.
В астрономии, задача о движении трёх тел, взаимно притягивающихся по закону тяготения и рассматриваемых как материальные точки. Классический пример задачи трёх тел - система Солнце, Земля, Луна. В 1912 финский астроном К. Ф. Сундман нашёл общее решение задачи трёх тел в виде рядов, сходящихся для любого момента времени t. Однако ряды Сундмана оказались совершенно бесполезными для практических вычислений вследствие их крайне медленной сходимости. При некоторых специальных начальных условиях можно получить очень простые решения задачи трёх тел (решения Лагранжа), представляющие большой интерес для астрономии. Частным случаем задачи трёх тел является так называемая ограниченная задача трёх тел, в которой два тела конечной массы движутся вокруг центра инерции по эллиптическим орбитам, а третье тело имеет бесконечно малую массу. Для ограниченной задачи удалось исследовать разнообразные классы периодических движений.
-
Задача двух тел.
Задача о движении двух тел, взаимно притягивающихся согласно закону тяготения. В задачи двух тел притягивающиеся тела принимаются за материальные точки, что справедливо, если они имеют сферическую структуру или если расстояния между ними весьма велики сравнительно с их размерами. Это условие в значительной мере выполняется для Солнца и каждой из планет. При решении задачи двух тел обычно рассматривают движение одного тела относительно другого. Движение в этой задаче происходит по коническим сечениям - окружности, эллипсу, параболе, гиперболе, прямой, - согласно законам Кеплера. Задача двух тел, описывающая так называемое невозмущённое движение, является первым приближением при изучении истинных движений небесных тел.
Глава 3. Методика организации научно - исследовательской работы школьников по небесной механике на примере моделей движения комет в гравитационном поле гауссовых колец
Методика организации научно - исследовательской работы школьников по небесной механике строится на основных педагогических принципах: системности, последовательности, целенаправленности и включает следующие этапы исследовательской деятельности:
1. Выбор темы исследования основывается на двух критериях: первый - субъективный: тема должна соответствовать интересам исследователя. Второй - объективный:
а) тема должна быть актуальной, то есть недостаточно изученной и важной в практических отношениях;
б) тема должна быть реально выполнимой, то есть надо иметь условия для успешного проведения работы (литература, материальное обеспечение, доступность объекта исследования, связь с учёными и т. д.).
Если школьник приступает впервые к работе, не знаком с достижениями в данной области, то выбор конкретной темы для него затруднителен и в этом случае ему необходима помощь со стороны учителя или консультация специалиста.
2. На втором этапе формулируется цель исследования. Она вытекает из формулировки темы исследования.
3. Формулировка задач исследования, то есть тех конкретных вопросов, на которые требуется получить ответ в процессе выполнения исследования. Правильно сформулированные задачи выполняют организационную и направляющую функции. Этот и последующие два этапа выполняются под руководством учителя, который корректирует, даёт рекомендации, выслушивает мнение ученика.
4. Написание программы исследования. Программа исследования включает следующие положения: обоснование актуальности и выбора темы, цель и задачи исследования, описание методики выполнения работы, календарный план и основное содержание работы.
5. Составление календарного плана. Делается общий план выполнения работы по срокам, чтобы школьник более ответственно относился к его выполнению. Для этого в плане ставятся сроки промежуточных отчётов, перед сверстниками, учителем, специалистом, а также родителями.
6. Знакомство с литературой по конкретной проблеме. Это необходимо для определения состояния изученности темы, выбора методов работы. Этот этап начинается с поиска литературы. Информацию об основных работах по теме педагог должен подготовить для ученика и рекомендовать самостоятельно изучить и выписать те научные источники, которые либо цитируются, либо прилагаются в конце научного издания. Помощь в поиске литературы может оказать и традиционный способ - просмотр каталогов библиотек. Важным источником библиографической информации являются справочные издания и словари. Наиболее эффективный путь - это консультации по данному вопросу со специалистами.
После нахождения необходимого литературного источника школьник приступает к работе с ним: делает библиографическую карточку (составляет свою картотеку по теме). Параллельно создаёт компьютерную базу данных.
Далее следует целенаправленное (исходя из задач исследования) конспектирование, выписывание цитат, методик. Это делается согласно ранее написанной, совместно с учителем, программы исследования.
После завершения работы с литературой школьник должен:
-
ориентироваться в выбранной области научного исследования, в том числе знать о степени изученности отдельных вопросов, о нерешённых проблемах, следовательно, может чётко оценить и сформулировать актуальность темы;
-
быть знаком теоретически с методиками исследования;
-
конкретизировать цель, скорректировать задачи исследования и план работы;
-
анализировать результаты своей работы, сравнивать полученные данные с таковыми других исследователей.
7. Выбор и освоение методики - «инструмента», посредством которого будут решаться основные вопросы проблемы путём постановки опыта, эксперимента или наблюдения в природе.
8. Выполнение основной части работы согласно выбранной методике.
9. Анализ результатов работы, сопоставление их с литературными и экспериментальными данными.
10. Оформление результатов исследования в виде таблиц, диаграмм и формулировка выводов. Выводы делаются на основе поставленных задач и полученных результатов. Это сложная часть научного исследования выполняется под руководством учителя, так как эта работа требует умения анализировать, сравнивать результаты, делать практические рекомендации на основе полученных результатов.
При написании работы требуется соблюдать ясность изложения, систематичность и последовательность подачи материала. Необходимо объяснить школьнику, что писать необходимо по возможности краткими и ясными предложениями, исключать тавтологию, частое повторение одних и тех же слов и выражений, научить, как нужно делать ссылки, приводить цитаты из источников, какой материал следует выносить в приложения. Учителю необходимо совместно со школьником работать над написанием текста, согласно плану и в соответствии с задачами исследования. При этом важно определиться с иллюстративным материалом. Выделить, какой из них пойдёт в приложение, какой необходим для иллюстрации основных положений работы.
Пример: модели движения комет в гравитационном поле гауссовых колец.
Небесномеханические модели эволюции траекторий комет
с возрастающей и убывающей массой
Введение
В настоящее время известно около 1500 потенциально опасных тел. Считается, что гибельным для Земли стало бы столкновение с ней тела размером в несколько километров, но и при падении полукилометрового тела - в зависимости от места падения - может оказаться, что некому будет вести спасательные операции, не будет дорог, коммуникаций, топлива и электроэнергии, иначе - наша цивилизация очень уязвима к космической угрозе, с точки зрения обширных внутренних связей.
Проблема астероидно-кометной опасности, по номенклатуре МЧС, является одной из 16 опасностей для России. (Полеты болидов над Ярославской областью уже зафиксированы).
Таким образом, углубленное изучение фундаментальных основ кометной космогонии и постановка соответствующих наблюдательных программ, при разработке систем раннего обнаружения опасных объектов и методов воздействия на них, подчеркивает актуальность исследования [1], [2].
В настоящее время возрастает интерес к интегрируемым задачам небесной механики [3].
В работе [4] рассматривается модель движения комет (с нулевой массой mk) типа Крейца в гравитационных полях Солнца массой mc и планет с массами mpi. Гравитационные поля тел, аппроксимировались полями гауссовых колец. Семейство Крейца - семейство околосолнечных, названное в честь астронома Генриха Крейца, который впервые показал их взаимосвязь. Этот группа комет с минимальными перигелийными расстояниями. Считается, что все они являются частями одной большой кометы, которая разрушилась несколько столетий назад. На примере Большой мартовской кометы 1843 года, в модели, найден интервал времени движения этой кометы от перигелия до афелия t=255.5288 лет. Эта величина соответствует (приближённо) половине периода движения рассматриваемой кометы (T=515.2126 лет). При этом принимались во внимание возмущения от Юпитера.
Целью данной работы является прогнозирование появления комет вблизи Земли, а также оценка степени их опасности.
Рассмотрим движение точки переменной массы при изотропном законе излучения в ньютоновском поле тяготения n - неподвижных концентрических колец - гауссовых колец [3] - вдоль оси аппликат.
Основные уравнения
Уравнение движения точки представим в виде
(1)
Допустим, масса кометы изменяется по закону
. (2)
Тогда,
(3)
В результате, с использованием метода Рунге-Кутта 4-ого порядка, получены следующие решения (3) -
z=z(t) - в графическом виде.
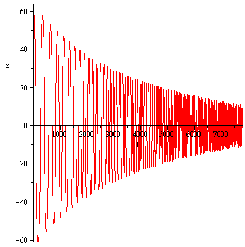
Рис.1 Движение кометы с возрастающей массой
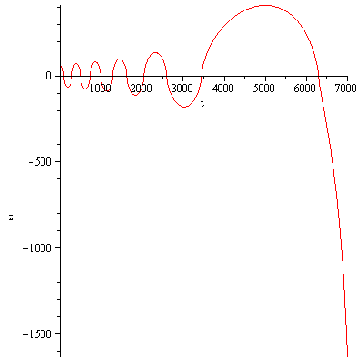
Рис.2 Движение кометы с убывающей массой
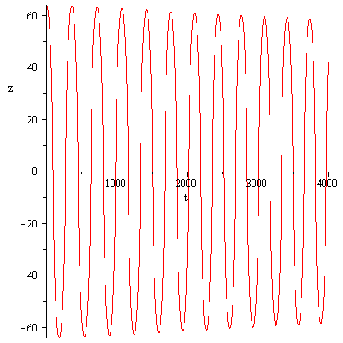
Рис.3 Движение кометы с постоянной массой
Заключение
1. Предложенные в работе модели орбитальной эволюции комет в гравитационном поле гауссовых колец позволяют оценивать периоды движения комет на основе новых квадратур дифференциальных уравнений движения, учитывающих возмущения [13], [14].
2. Из наблюдений и расчетов следует - при соединении Сатурна и Юпитера центр масс системы Солнце-Юпитер-Сатурн всегда находится за Солнцем, что способствует естественной защите Земли от ряда небесных тел.
3. При потере массы кометой, она выбрасывается из Солнечной системы.
4. При поглощении кометой окружающей материи, она приближается асимптотически к центру Солнечной системы.
5. При постоянной массе, в данной модели, комета совершает периодические колебания относительно центра масс системы.
По мнению автора, данная работа представляет интерес для разработки теоретических методов локализации в пространстве-времени неидентифицированных метеорных потоков, неоткрытых комет и разработки новых критериев отождествления опасных небесных тел [14].
Глава 4. Анализ школьной литературы.
В большинстве российских школ предмет «астрономия» фактически поставлен вне закона - под предлогом того, что ни один из учебников астрономии не был разрешён и допущен к использованию в школах. Прямого запрета изучать в школах астрономию нет, в некоторых же школах этот предмет преподают в качестве спецкурсов.
Мы решили произвести анализ школьной литературы, в которой встречаются темы по астрономии.
-
Пёрышкин А.В. Физика. 7 класс: Учебник для образовательных учреждений.
Материал для дополнительного чтения.
§2. Невесомость.
§3. Сила тяжести на других планетах.
-
Пёрышкин А.В. Физика. 8 класс: Учебник для образовательных учреждений.
Материал для дополнительного чтения.
§2. Использование энергии Солнца на Земле.
-
Физика и астрономия: Учеб. для 8 класса общеобразоват. учреждений / А. А. Пинский, В. Г. Разумовский, Н. К. Гладышева и др.; Под ред. А. А. Пинского, В. Г. Разумовского. - 5-е изд. - М.: Просвещениеы, 2001.
Глава VI. Природа тел солнечной системы.
§6.1. Солнце и его роль в Солнечной системе.
§6.2. Две группы планет. Происхождение Солнечной системы.
§6.3. Земля и её спутник Луна.
§6.4. Планеты земной группы.
§6.5. Планеты - гиганты, их спутники и кольца.
§6.6. Малые тела Солнечной системы: астероиды, метеориты, кометы.
-
Физика и астрономия: Учеб. для 7 класса общеобразоват. учреждений / А. А. Пинский, В. Г. Разумовский, Ю. И. Дик и др.; Под ред. А. А. Пинского, В. Г. Разумовского. - 5-е изд. - М.: Просвещение, 2001.
Глава 1. Физика и астрономия - науки о природе.
§1.1. Природа и человечество. Физика.
§1.2. Астрономия - наука о небесных телах.
-
Физика. 9 класс. Пинский А.А., Разумовский В.Г. - 4-е изд. - М.: 2003. - 303 с.
Глава 6. Движение небесных тел. Системы координат
§6.1. Положение материальной точки в простанстве и система координат.
§6.2. Небесные координаты.
§6.3. Кульминации звёзд. Определение местного времени и географических координат.
§6.4. Продолжительность суток и календарь.
§6.5. Определение расстояний до тел Солнечной системы и их размеров.
§6.6. Движение планет Солнечной системы. Законы Кеплера.
Глава 9. Строение и эволюция Вселенной.
§9.1. Мир звёзд.
§9.2. Наша Галактика.
§9.3. Галактики и квазары.
§9.4. Большой взрыв.
Глава 5. Заключение.
На протяжении многих тысячелетий основы астрономических знаний - основы представлений о Вселенной входили в систему подготовки подрастающих поколений. В монастырских школах средневековья астрономия наряду с геометрией, арифметикой входила в «квадривиум».
В настоящее же время возникает вопрос - почему же изучение астрономии в средней школе актуально? Прежде всего, это необходимо современному образованному человеку в силу тех важных социальных функций, которые выполняет астрономия на протяжении всей истории человечества и в которые современная эпоха вносит новые грани. Первая из этих функций - прикладная.
Вторая функция - общекультурная: определение места и роли человека в структуре Вселенной.
Астрономическая картина мира на протяжении тысячелетий была и есть неотъемлемой составной частью научной картины мира в целом; той ее частью, которая дает человеку представление о пространственно-временной структуре мира, в котором он живет и действует.
Да и вообще, что нужно доказывать, если мы первые создали космические корабли, первые преодолели земное притяжение! Мы первые покорили космос! Мы первые вышли в открытый космос! Именно наши ракеты "Протон" выводят спутники любых стран на орбиты! Россия готовит космонавтов любых стран! Космонавтика - одно из немногих направлений науки, где мы ещё сохраняем лидирующие позиции в мире.
И всё это потому, что астрономия, преподаваемая в школах, открывала детям прекрасный и загадочный мир Вселенной! Именно из бывших школьников, влюбившихся в звездное небо, вышли талантливые конструкторы и космонавты! Учёные международного уровня! И очень обидно, что именно теперь, когда весь остальной цивилизованный мир увлекся астрономией, мы - перестали преподавать её в школе.
Поэтому и возникает необходимость проведения элективных курсов, на которых школьники смогут заняться проектной деятельностью, организация научной работы, дополнительных занятий по астрономии в частности в разделе небесной механики, астрономические кружки.
Глава 6. Список литературы.
-
Пёрышкин А.В. Физика. 7 класс: Учебник для образовательных учреждений. 7-е изд., стереотип. - М.: Дрофа, 2003. - 192 с: ил.
-
Пёрышкин А.В. Физика. 8 класс: Учебник для образовательных учреждений. - 15-е изд., стереотип. - М.: Дрофа, 2012. - 191, [1] с. : ил.
-
Генденштейн Л.Э., Дик Ю.И. Физика. 10 класс: Учебник базового уровня для общеобразовательных учебных заведений. - 3-е изд. - М.: ИЛЕКСА, 2008. - 288 с.: ил.
-
Мякишев Г.Я., Буховцев Б.Б. Физика: Учебник для 10 кл. сред. Шк. - 9-е изд., перераб. - М.: Просвещение, 1987. - 319 с., 4 л. Ил.: ил.
-
Генденштейн Л.Э. Физика. 7 класс. В 2 ч. Ч.1: учебник для общеобразовательных учреждений/ Л.Э.Генденштейн, А.Б.Кайдалов; под ред. В.А. Орлова, И.И. Ройзена. - 3-е изд., испр. - М.: Мнемозина, 2012. - 255 с.: ил.
-
«Современная астрономия и методика её преподавания» Материалы IV Всероссийской научно - практической конференции 24-26 марта 2004 г. РГПУ им. А.И.Герцена
-
Физика и астрономия: Учеб. для 8 класса общеобразоват. учреждений / А. А. Пинский, В. Г. Разумовский, Н. К. Гладышева и др.; Под ред. А. А. Пинского, В. Г. Разумовского. - 5-е изд. - М.: Просвещениеы, 2001.
-
Физика и астрономия: Учеб. для 7 класса общеобразоват. учреждений / А. А. Пинский, В. Г. Разумовский, Ю. И. Дик и др.; Под ред. А. А. Пинского, В. Г. Разумовского. - 5-е изд. - М.: Просвещение, 2001.
-
Физика. 9 класс. Пинский А.А., Разумовский В.Г. - 4-е изд. - М.: 2003. - 303 с.
-
Перов, Н.И. Малые небесные тела: миграция и поиск [Текст]. - LAP LAMBERT Academic Publishing GmbH&Co.KG.Saarbrucken, 2010. - 300с.
-
Перов, Н.И. и др. Теоретические методы локализации в пространстве - времени неоткрытых небесных тел [Текст]. - Ярославль: Изд-во ЯГПУ, 2011. - 208 с.
-
Вашковьяк, М.А., Вашковьяк, С.А. Силовая функция слабоэллипти ческого гауссова кольца и её обобщение на почти компланарную систему колец [Текст] // Астрономический вестник РАН, 2012. Т. 46. №1. С.72-80.
-
Модулина Д.Г. Интегрируемый случай задачи о движении частицы с постоянной массой в гравитационном поле гауссовых колец [Текст] / «Космонавтика и общество: проблемы и решения». Сборник материалов Всероссийской научно-практической конференции, посвященной юбилею первой женщины - космонавта В.В.Терешковой. Сост. Перов Н.И., Тихомирова Е.Н. Ярославль: МАУ г. Ярославля «КПЦ им. В.В.Терешковой», 2012. С. 48-51.
-
Modulina,D.G., Tikhomirova,E.N. On the Models of Cometary's Orbits Evolution. // 44th Lunar and Planetary Science Conference, held March 18-22, 2013 in The Woodlands, Texas. LPI Contribution No. 1719. P.1103.
17