Учебный материал по теоретической механике. часть 1. Статика. Сборник заданий для самостоятельного выполнения расчетно-графических работ. Методические указания (для изучения теоретического курса, практических и лабораторных занятий) для студентов очной и

Депобразования и молодежи Югры

бюджетное учреждение профессионального образования

Ханты-Мансийского автономного округа - Югры

«Мегионский политехнический колледж»

(БУ «Мегионский политехнический колледж»)

Преподаватель физики и технической механики

Магомедов А.М.

Учебный материал по теоретической механике.

часть 1.

Статика.

Сборник заданий для самостоятельного выполнения расчетно-графических работ.

Методические указания (для изучения теоретического курса, практических и лабораторных занятий) для студентов очной и заочной форм обучения.

Направление: Специальность 131018 Разработка и эксплуатация нефтяных и газовых месторождений.

Мегион, 2016

Депобразования и молодежи Югры

бюджетное учреждение профессионального образования

Ханты-Мансийского автономного округа - Югры

«Мегионский политехнический колледж»

(БУ «Мегионский политехнический колледж»)

Преподаватель физики и технической механики

Магомедов А.М.

Учебный материал по теоретической механике

часть 1

Статика

Сборник заданий для самостоятельного выполнения расчетно-графических работ

методические указания (для изучения теоретического курса, практических и лабораторных занятий) для студентов очной и заочной форм обучения.

Направление: Специальность 131018 Разработка и эксплуатация нефтяных и газовых месторождений.

Мегион,2016

ОГЛАВЛЕНИЕ

ВВЕДЕНИЕ

Одной из ведущих дисциплин высшей технической школы является теоретическая механика - наука о механическом движении и взаимодействии материальных тел. Законы теоретической механики лежат в основе фундаментальных, прикладных и специальных наук.

Теоретическая механика включает в себя три основных раздела: статика, кинематика и динамика.

Статика - это раздел механики, в котором решается две основные задачи: приведение системы сил к эквивалентной и установление условий равновесия исследуемой системы сил.

В общем курсе теоретической механики изучают механику материальной точки, механику твердого тела и механику системы материальных точек. Роль и значение теоретической механики состоит в том, что ее законы и методы позволяют изучить ряд важных явлений в окружающем мире.

В пособии рассматриваются основные теоретические вопросы разделов механики, а так же дано подробное решение наиболее важных задач из контрольных работ по статике, при этом, следует уделить особое внимание тем задачам, которые будут предложены студентам на экзамене.

По каждому разделу теоретической механики представлены контрольные задания по ряду задач для расчетно-графических работ, которые могут выполняться на практических занятиях или выдаваться как домашние задания, а так же могут быть использованы в качестве контрольных заданий для заочного обучения.

Выбор задач осуществляется по вариантам, указанным преподавателем (для очного обучения), или по двум последним цифрам личного шифра (для заочного обучения).

Пособие содержит по 30 вариантов заданий по 4 темам статики. Цель работы - закрепить теоретический материал программы и приобрести твердые навыки решения задач по теоретической механике.

1. СТАТИКА

1.1. Основные понятия и определения

Материальная точка - это модель материального тела, формами и размерами которой при решении данной задачи можно пренебречь.

Механическая система - это совокупность материальных точек.

Абсолютно твердое тело - это механическая система, расстояние между точками которой не изменяется при любых взаимодействиях.

Сила - это мера воздействия одного материального тела на другое, является векторной величиной и характеризуется точкой приложения, направлением и числовым значением (модуль силы).

Система сил - это совокупность сил, действующих на некоторое тело.

Плоская произвольная система сил - система сил, как угодно расположенных, в одной плоскости. Для равновесия любой системы сил необходимо и достаточно, чтобы главный вектор этой системы сил и ее главный момент относительно любого центра О были равны нулю, то есть чтобы выполнялись условия

,

Первая (основная) форма условий равновесия: для равновесия плоской произвольной системы сил необходимо и достаточно, чтобы алгебраическая сумма проекций всех сил на каждую из координатных осей и и алгебраическая сумма моментов этих сил относительно любой точки О, лежащей в плоскости действия сил, были равны нулю, то есть

, ,

Вторая форма условий равновесия: для равновесия плоской произвольной системы сил необходимо и достаточно, чтобы алгебраическая сумма проекций всех сил на одну из координатных осей, а так же алгебраические суммы моментов этих сил относительно двух любых точек, лежащих в плоскости действия сил, были равны нулю, то есть

, ,

Прямая АВ не должна быть перпендикулярна оси .

Третья форма условий равновесия: для равновесия плоской произвольной системы сил необходимо и достаточно, чтобы алгебраические суммы моментов этих сил относительно трех любых точек, лежащих в плоскости действия сил, были равны нулю, то есть

, ,

Точки А, В, С не должны лежать на одной прямой.

Пространственная произвольная система сил - система сил, как угодно расположенных в пространстве. Для равновесия любой системы сил необходимо и достаточно, чтобы

,, , ,,

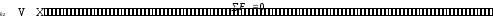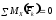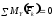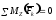
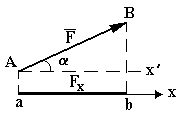
Проекцией силы на ось называют отрезок, заключенный между перпендикулярами, опущенными из начала и конца вектора силы на эту ось.

Моментом силы относительно любой точки О называется произведение модуля силы на плечо, взятое со знаком плюс или минус.

Плюс берется, если сила стремится повернуть тело вокруг точки О против хода часовой стрелки, минус, - если, - по ходу часовой стрелки.

Плечо - кратчайшее расстояние от точки поворота О до линии действия силы.

Если линия действия силы пересекает точку О, то ее момент относительно этой точки равен нулю, так как .

так как .

При определении момента силы может вызвать трудность вычисление плеча . Поэтому, чтобы упростить эту задачу, надо:

а) разложить силу на ее составляющие и параллельно выбранным осям и ;

б) применить теорему Вариньона: , момент равнодействующей силы относительно точки О равен алгебраической сумме моментов составляющих ее сил относительно той же точки О или

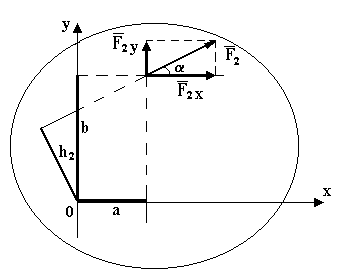
Парой сил называют две силы и равные по величине, противоположно направленные и параллельные между собой.

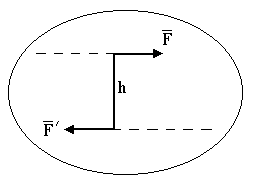
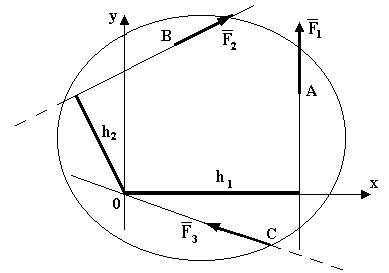
Моментом пары сил называют произведение модуля одной из сил пары на плечо, взятое со знаком плюс или минус, то есть

.

Момент пары считается положительным, если пара, в плоскости ее действия, стремится повернуть тело против хода часовой стрелки, и отрицательным, если, - по ходу.

Плечо пары _h - кратчайшее расстояние между линиями действия пары.

Распределенные силы - система сил распределенных вдоль поверхности по тому или иному закону. Плоская система распределенных сил характеризуется ее интенсивностью - значение силы, приходящейся на единицу длины нагруженного отрезка. Измеряется в ньютонах, деленных на метр (Н/м). При составлении расчетной схемы распределенную нагрузку заменяют сосредоточенной силой Q.

Силы равномерно распределенные вдоль отрезка прямой

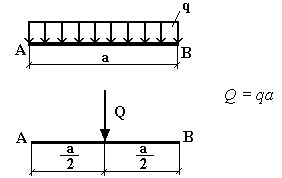
Силы распределенные вдоль отрезка прямой по линейному законуВ большинстве случаев твердое тело не может произвольно перемещаться в пространстве, так как его свобода ограничена. Тела, ограничивающие свободное перемещение рассматриваемого тела, называют связями. В результате взаимодействия тела и наложенной на него связи возникают силы, которые называют реакциями связей. В процессе решения задачи связи, наложенные на тело, заменяют их реакциями, что называют принципом освобождения от наложенных связей. На расчетных схемах связи изображают условно. В таблице представлены наиболее часто встречающиеся типы связей.

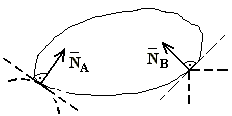
Типы связей. Реакции связейгладкая поверхность (точка А) и уступ (точка В)

Реакция гладкой поверхности направлена по общей нормали к поверхностям соприкасающихся тел. Реакция уступа направлена по нормали к поверхности опирающегося тела.

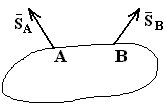
2. Нить

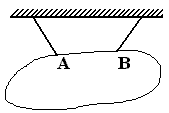
Реакция направлена вдоль нити от тела (нить работает только на растяжение)

3. Невесомый стержень с шарнирами на концах

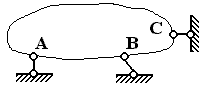
Реакция направлена вдоль стержня, стержень работает либо на растяжение, либо на сжатие.

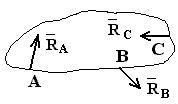
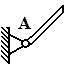
4. цилиндрический шарнир (подшипник)

А - ось подшипника перпендикулярна чертежу

Составляющие реакции лежат в плоскости, перпендикулярной оси шарнира.

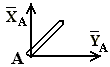
5. подвижная шарнирная опора (на катках)

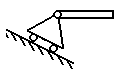
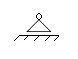
Реакция направлена перпендикулярно опорной плоскости

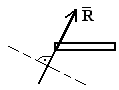
6. Заделкаа) жесткая

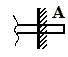
б) скользящая

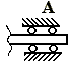
Реакции при действии на тело плоской системы сила) жесткая

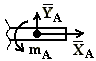
б) скользящая

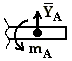
Очень часто приходится определять центр тяжести различных плоских фигур сложной формы, пространственной решетки, а так же центр тяжести объемных фигур.

При определении центра тяжести можно использовать некоторые особенности тела.

Для однородного тела, имеющего центр симметрии, ось симметрии или плоскость симметрии задача нахождения центра тяжести упрощается. Он находится соответственно в центре симметрии, на оси симметрии или на плоскости симметрии.

Возможно, также использовать метод разбиения или дополнения. При этом тело разбивается на тела или дополняется до тел, центр тяжести которых легко определяется.

Центр тяжести плоской геометрической фигуры определяется по формуле:

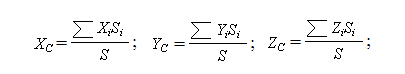
где (X_C ;Y_C ;Z_C ) - координаты центра тяжести тела,

(X_i ;Y_i ;Z_i ) - координаты центра тяжести части тела,

S_i - площадь части тела,

S - площадь тела.

Центр тяжести пространственной решетки определяется по формуле:

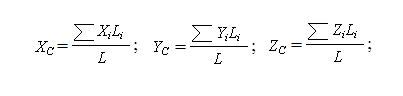
где L_i - длина стержня,

L - длина стержней тела

Центр тяжести объемной фигуры определяется по формуле:

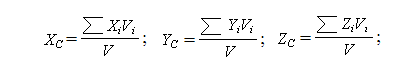
где V_i - объем части тела,

V - объем тела.

Умение рассчитывать фермы является важной инженерной задачей, а изучение методов их расчетов является многоплановой задачей. Известны три метода расчета ферм: метод вырезания узлов, метод сечений (метод Риттера) и графический метод. В данном пособии рассмотрены только первые два метода, носящих аналитический характер.

1.2. Определение реакций опор составной системы

1.2.1. Пример выполнения расчетно-графической работы

1.Исходные данные. Исходная схема системы двух тел показана на рисунке.

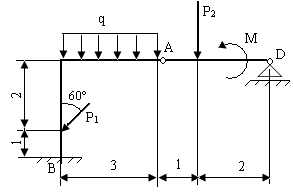
Дано: P₁ = 6кН, P₂ = 10 кН, М = 25кН∙м, q = 0,8кН/м. Линейные размеры указаны в метрах.

2.Классификация связей. A - гладкий цилиндрический шарнир, B - жесткая заделка, D - подвижная шарнирная опора.

3.Расчетная схема.

Для системы в целом:

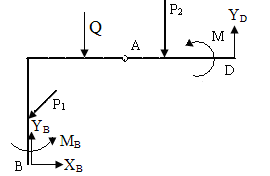
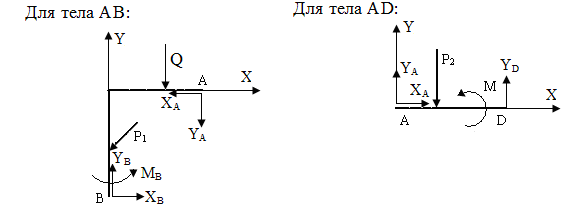
4.Условия равновесия.

Для тела AB: ∑X_i = X_B - P₁ sin60º - X_A = 0

∑Y_i = Y_B - P₁ cos60º - Y_A = 0

∑M_Bi = M_B + P₁ sin60º - 1,5 Q + 3X_A - 3Y_A = 0

Для тел AD: ∑X_i = X_A = 0

∑Y_i = Y_A - P₂ + Y_D = 0

∑M_Ai = -P₂ + M + 3Y_D = 0

5. Определение реакций связей.

X_B - 6∙0,86 - X_A = 0

Y_B - 6∙0,5- Y_A = 0

M_B + 6∙0,86 - 1,5∙0,8∙3 + 3X_A - 3Y_A = 0

X_A = 0

Y_A - 10 + Y_D = 0

-10 + 25 + 3Y_D = 0

6. Итоговые расчетные данные.

X_A = 0; Y_A = 25кН; X_B = 5,16кН; Y_B = 28кН; Y_D = -15кН; M_B = 73,44кН∙м

1.3. Произвольная пространственная система сил

1.3.1. Пример выполнения расчетно-графической работы

1. Исходные данные. Определить значение силы натяжения T и реакции опор A и B пространственной конструкции, изображенной на рисунке.

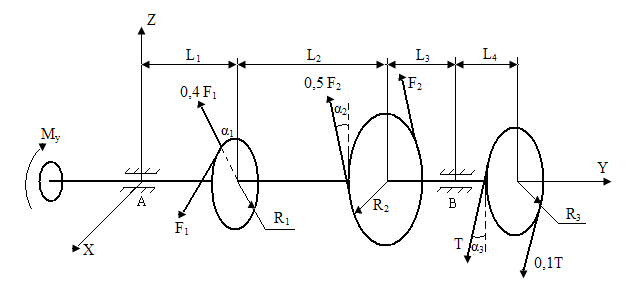
Дано: F₁ = 10кН, F₂ = 6кН, L₁ = 0,5м, L₂ = 1м, L₃ = 0,4м, L₄ = 0,3м,

α₁ = 30º, α₂ = 60º, α₃ = 30º, R₁ = 0,5м, R₂ = 0,8м, R₃ = 0,6м, M₄ = 14кН∙м.

2. Расчетная схема.

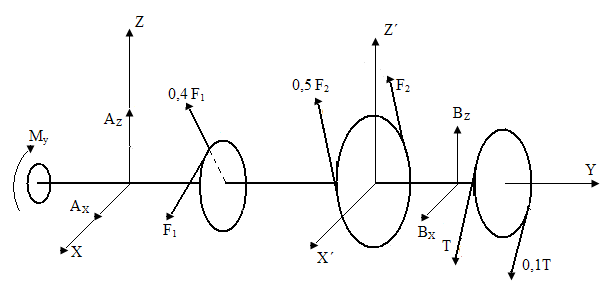
3. Условия равновесия.

∑M_X = F₁∙0,5(sin30º + 0,4cos30º)- F₂∙1,5cos60º∙1,5-B_Z∙1,9 + Tcos30º∙2,2∙1,1=0

∑M_Y = M_Y - 0,5F₁ + 0,5F₂∙0,8 - F₂∙0,8 - T∙0,6 + 0,1T∙0,6 = 0

∑M_Z = F₁∙0,5(cos30º- 0,4sin30º) +F₂∙1,5sin60º∙1,5 +T∙sin30º∙2,2∙1,1 +B_X∙1,9=0

∑F_iX = A_X + F₁(cos30º - 0,4sin30º) + 1,5F₂sin60º + B_X + Tsin30º∙1,1 = 0

∑F_iZ = A_Z - F₁(sin30º + 0,4cos30º) + 1,5F₂cos60º + B_Z - Tcos30º∙1,1 = 0

4. Определение реакций связей.

2,2T - 1,9B_Z = 2,4; T = 13кН; B_X = -14кН; A_X = -8кН; A_Z = 2кН

6. Итоговые расчетные данные.

T = 13кН; B_Z = 14кН; B_X = -14кН; A_X = -8кН; A_Z = 2кН

1.4. Расчет плоских ферм

1.4.1. Пример выполнения расчетно-графической работы

1. Исходные данные. Определить реакции связей фермы от заданной нагрузки, усилия во всех стержнях методом вырезания узлов, а так же в стержнях, отмеченных знаком V , определить усилия методом сечения.

P₁ = 5кН, P₂ = 5кН, P₃ = 5кН, α = 30º, a = 1м.

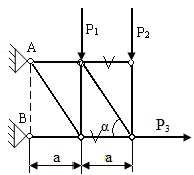
2. Расчетная схема для реакций связей.

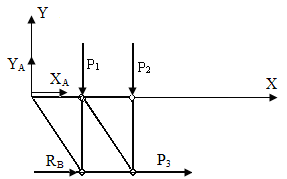
3. Условия равновесия.

∑M_A = R_B∙a∙tgα + P₃∙a∙tgα - P₁∙a - P₂∙2a = 0

∑F_X = R_B + P₃ + X_A = 0

∑F_Y = Y_A - P₁ - P₂ = 0

4. Определение реакций связей.

0,57R_B + 2,85 - 5 - 10 = 0; R_B + 5 + X_A = 0; Y_A - 5 - 5 = 0

Тогда R_B = 21,32кН; X_A = -26,32кН; Y_A = 10кН

5. Метод вырезания узлов_.

Пронумеруем все стержни фермы.

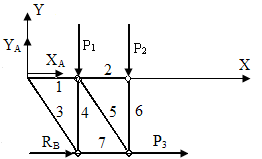
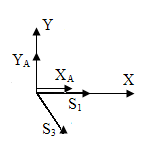
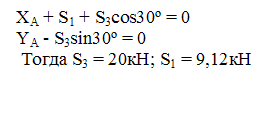
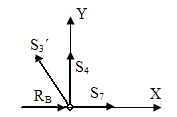
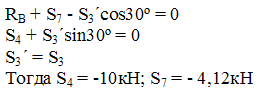
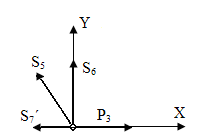
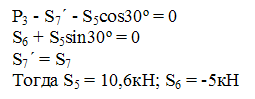
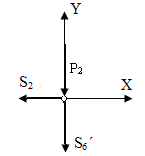
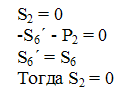
6. Метод сечений.

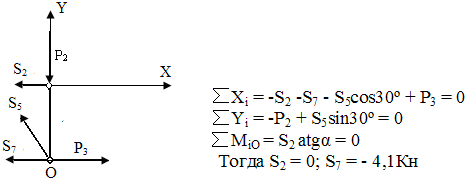
1.5. Центр тяжести сил

1.5.1. Пример выполнения расчетно-графической работы

1. Исходные данные. Определить центр тяжести пространственной решетки и плоской геометрической фигуры.

2. Пространственная решетка.

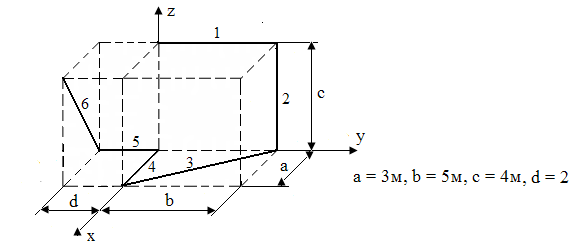
L₁ = 5; X₁ = 0; Y₁ = 2,5; Z₁ = 4;

L₂ = 4; X₂ = 0; Y₂ = 5; Z₂ = 2;

L₃ = √3² + 5² = 5,8; X₃ = 1,5; Y₃ = 2,5; Z₃ = 0;

L₄ = 3; X₄ = 3; Y₄ = 0; Z₄ = 0;

L₅ = 2; X₅ = 0; Y₅ = -1; Z₅ = 0

L₆ = √3² + 4² = 5; X₆ = 1,5; Y₆ = -1; Z₆ = 2

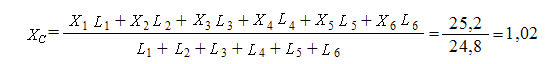
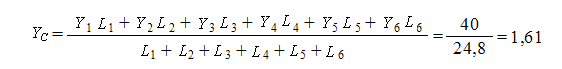
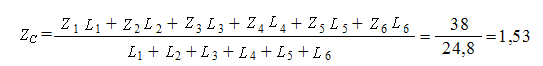
Тогда C(1,02; 1,61; 1,53)

3. Плоская геометрическая фигура

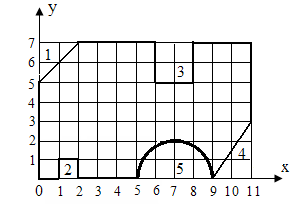
S₁ = 2; X₁ = (0+0+2)/3=0,67; Y₁ = (0+7+7)/ 3= 4,67

S₂ = 1; X₂ = 1,5; Y₂ = 0,5

S₃ = 4; X₃ = 7; Y₃ = 6

S₄ = 3; X₄ = (0+11+11)/3= 7,33; Y₄ = (0+0+3)/3=1

S₅ = π2²/2 = 6,28; X₆ = 7; Y₆ = ⅔ 2sin90º/(π/2) = 0,85

S = 77; X = 5,5; Y = 3,5

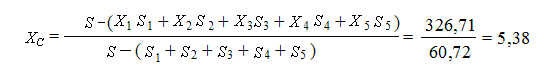
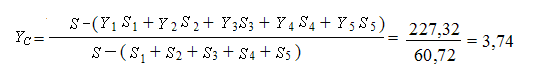
Тогда C(5,38; 3,74)

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Теоретическая механика. Терминология [Текст]. Вып. 90. М.: Наука, 2016.-40с.

2. Тарг, С.М. Краткий курс теоретической механики [Текст]: учеб. для втузов/ С. М. Тарг. 14-е изд, стер.-М.: Высш. шк., 2014.-416с.

3. Попов, М.В. Теоретическая механика. Краткий курс [Текст]: учеб. для втузов/ М. В. Попов. - М.: Наука, 2016.-336с.

4. Мещерский, И.В. Сборник задач по теоретической механике [Текст]: учеб. Для втузов/ И.В.Мещерский. - М.: Наука, 2016.-447с.

5. Яблонский, А.А. Курс теоретической механики [Текст]: учеб. для втузов/ А.А.Яблонский, В.М.Никифорова. - М.: Высш. шк., 2014. -Ч.1.-343с.

</