План открытого урока по физике/математике на тему Баллистическое движение

Интегрированный урок (математика, физика) по теме «Баллистическое движение».

Авторы урока: учитель математики кадетского корпуса (инженерной школы) ВУНЦ ВВС «ВВА» Богданова И.В., учитель физики кадетского корпуса (инженерной школы) ВУНЦ ВВС «ВВА» Ветохина Т.Н.

Техника давно познала высокую цену науки

и ее влиянию обязана своим современным блестящим развитием

Н. Жуковский.

ТИП УРОКА: Урок «открытия» нового знания.

ЦЕЛЬ УРОКА: Деятельностная цель: формирование у учащихся умений реализации новых способов действия.

Содержательная цель: расширение понятийной базы за счет включения в нее новых элементов.

ЗАДАЧИ УРОКА:

Образовательные:

- Раскрыть основные свойства баллистического движения, опираясь на метапредметные связи курсов физики - математики и продолжив формировать представление об окружающем нас мире, природе, как о едином целом.

-Совершенствовать ЗУН учащихся.

- Развивать у учащихся интереса к предмету.

Развивающие:

- Развивать коммуникабельность.

- Развивать исследовательские навыки учащихся.

Воспитательные:

- Воспитывать уверенность в своих силах.

- Воспитывать потребность трудиться.

- Воспитывать способности исполнять законы через ответственность за окружающих.

ОБОРУДОВАНИЕ К УРОКУ: учебник, диски «Открытая физика» и «Открытая математика», презентация, компьютер, проектор.

Ход урока:

1. Этап мотивации (самоопределения) к учебной деятельности.

Звучит музыка. Учителя приветствуют учащихся. Объявляют цели и задачи урока.

2. Этап актуализации и пробного учебного действия;

Учитель физики.

В многочисленных войнах на протяжении всей истории человечества, враждующие стороны, доказывая своё превосходство, использовали сначала камни, копья, и стрелы, а затем ядра, пули, снаряды, и бомбы. Успех сражения во многом определялся точностью попадания в цель. При этом точный бросок камня, поражение противника летящим копьём или стрелой фиксировались воином визуально. Это позволяло при соответствующей тренировке повторять свой успех в следующем сражении. Желание побеждать стимулировало появление баллистики (от греческого слова ballo-бросаю). Артиллерийское (затем ракетно-артиллерийское) вооружение являлось важнейшей составляющей военной мощи России на всех этапах ее существования. На решение теоретических проблем, возникающих в процессе развития ракетно-артиллерийского вооружения (РАВ), была нацелена баллистика - одна из основных военно-технических дисциплин. Ее развитие всегда находилось в зоне особого внимания военных ученых.

3) Изучение новых знаний и способов деятельности.

Учитель физики. Давайте проанализируем, как же развивалась баллистика.

Доклад учащихся. История баллистики тесно связана с историей развития артиллерии. Ряд выдающихся ученых, особенно математиков, занимался вопросами баллистики еще до средних веков. К ним относятся Галилей, Торричелли, Мерсен, Ломоносов, Эйлер, Бернулли. Именно Мерсен в 1644 г. предложил назвать науку о движении снаряда баллистикой.

5-6 слайд. Как самостоятельная, определённая область науки, баллистика получила широкое развитие с середины XIX века. Баллистика многим обязана трудам великих русских математиков Н.И. Лобачевского, П.Л. Чебышева, М.В. Остроградского, замечательным работам воспитанников Михайловской артиллерийской академии А.А. Фадеева, Н.В. Майевского, Н.А. Забудского, В.М. Трофимова, Н.Ф. Дроздова и др.

7 слайд. В 1721 г. член Петербургской Академии Наук Даниил Бернулли решил задачу о движении снаряда с учётом силы сопротивления воздуха. Он принимал эту силу пропорционально квадрату скорости снаряда.

8 слайд. Первое настоящее решение основных задач баллистики дал знаменитый математик Эйлер. В 1753 г. Эйлер дал более простое решение задачи о движении снаряда в воздухе и предложил метод расчёта траекторий, который применяется до настоящего времени.

9 слайд. В нашей стране после Великой Октябрьской социалистической революции была создана Комиссия особых артиллерийских опытов. В Комиссию были привлечены выдающиеся ученые: А.Н. Крылов, С.А. Чаплыгин, Н.Е. Жуковский В Комиссии были подробно разработаны вопросы сверхдальнобойной стрельбы (до 140 км).

</ 10 слайд. Никола́й Его́рович Жуко́вский - русский механик, создатель аэродинамики как науки. Заслуженный профессор Московского университета, профессор теоретической механики Императорского Московского технического училища. Работы Жуковского в области аэродинамики явились источником основных идей, на которых строится авиационная наука. Он всесторонне исследовал динамику полёта птиц, 3 ноября 1891 года сделал доклад «О парении птиц». В 1892 году составил основные уравнения динамики для центра тяжести планирующего тела, Жуковский нашёл траектории при различных условиях движения воздуха, в том числе теоретически предсказал возможность мёртвой петли.

11 слайд. В Советском Союзе центром артиллерийской науки являлась Артиллерийская академия им. Дзержинского. За это время в СССР проведены выдающиеся работы по внешней баллистике. Профессором Пугачёвым решена общая задача о движении вращающегося снаряда в воздухе. В нашей стране создана и осуществлена на практике теория реактивного движения, основы которой были заложены в работах К. Э. Циолковского и И. В. Мещерского.

Учитель физики. Для описания баллистического движения удобнее всего рассмотреть модель «Движение тела, брошенного под углом к горизонту». В условиях данной модели тело будем рассматривать как материальную точку, движущуюся с постоянным ускорением свободного падения, при этом пренебрегая сопротивлением воздуха, кривизной поверхности Земли и ее вращением вокруг собственной оси.

Это приближение существенно облегчает расчет траектории тел. Однако такое рассмотрение имеет определенные границы применимости. Например, при полете межконтинентальной баллистической ракеты нельзя пренебрегать кривизной поверхности Земли и не учитывать сопротивление воздуха. Но для достижения поставленной цели в условиях данной модели мы можем пренебречь вышеуказанными величинами. Итак, давайте вспомним основные уравнения, позволяющие описывать движение тела, брошенного под углом к горизонту.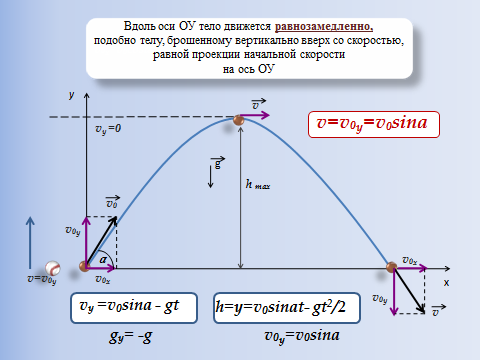

Учитель математики. Давайте вспомним схему исследования функции. Для этого предлагаю сформулировать свойства, которые объединяют функции в пары.

19 слайд

Область определения;

Множество значений;

Нули функции;

Монотонность;

Промежутки монотонности;

Функция принимает каждое свое значение дважды, за исключением единственной точки.

20 слайд

Учитель математики. Перед нами три параболы. Назовите отличительные особенности каждой функции.

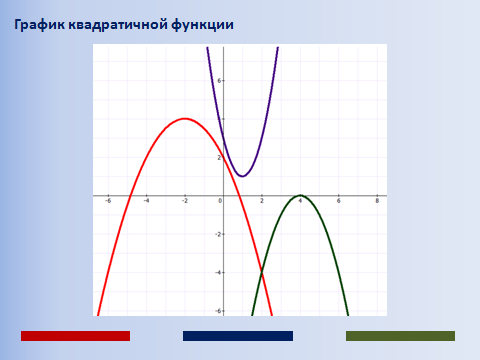
Дискриминант положительный;

Дискриминант отрицательный;

Дискриминант равен нулю.

21 слайд

4) Первичное закрепление.

Учащиеся получают задания для исследования в группах. Выделяются три группы

1.Практики решают предложенную учителем задачу с точки зрения физики.

Найти высоту подъёма и дальность полёта сигнальной ракеты, выпущенной со скоростью 40 м/с под углом 60⁰ к горизонту. Написать уравнение траектории.

2. Математики по предложенным уравнениям, зависимости координат от времени получают уравнение траектории и строят график.

3. Теоретики исследуют полученный математиками график траектории.

После этого каждая группа представляет полученный результат на интерактивной доске.

5) Выступление представителей групп:

1. Практики предлагают решение задачи и как результат своей работы записывают уравнение траектории.

2. Математики предлагают исследование функции:

Область определения функции;

Множество значений функции;

Наибольшее значение функции. Функция принимает каждое свое значение дважды, исключение составляет только единственная точка, в которой функция принимает свое наибольшее значение;

Нули функции.

Представляют график функции.

22 слайд

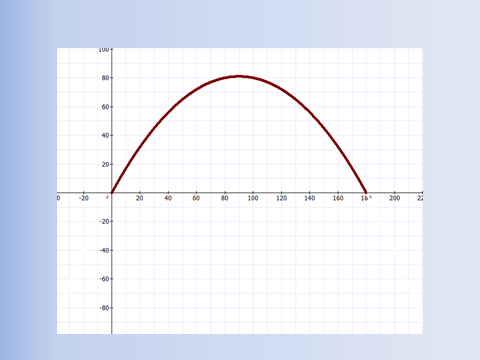
Представление результатов работы группы исследователей. Начинаем с вопросов: Зависит ли дальность полета от выбранного угла?

При каких значениях α дальность полета одинаковая?

При каком значении α дальность полета наибольшая?

23 слайд

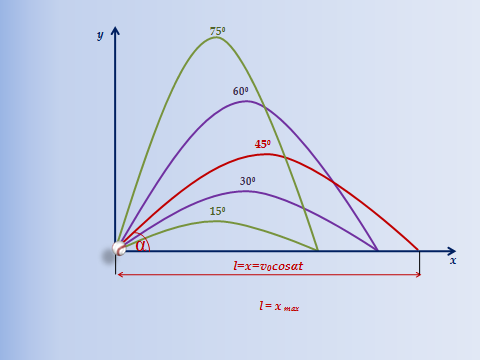
24 слайд

Рассмотрим для значения α=15⁰. Значение синусов углов 30⁰ и 150⁰ одинаковые. Этот факт объясняется формулами приведения.

25 слайд

Имеем функцию . Как уже упоминалось, нули этой функции: и . Применяя формулы тригонометрии можно преобразовать . Будем иметь . Учитывая ограниченность синуса, несложно заметить, что наибольшего своего значения 1 он будет достигать при значении α = 45⁰.

Вывод: дальность полета одинаковая для углов, дополняющих друг друга до 90⁰. Дальность полёта максимальна для α = 45⁰.

5) Рефлексия. На интерактивную доску выводится таблица.

Учащиеся подходят к доске и с помощью магнитов выбирают любые два утверждения, которые соответствуют их впечатлениям, полученным на уроке. По количеству магнитов в каждой колонке учителя могут судить о полноте достижения целей, поставленных в начале урока.