Нахождение наибольших и наименьших значений физических величин

Урок по теме:

«Нахождение наибольших и наименьших значений физических величин».

(11 класс спецкурс).

Первый урок занятия.

Тип урока: комбинированный урок получения новых знаний.

Форма проведения урока - поисковая беседа.

Цель урока - продолжить совершенствование навыков решения задач.

Задачи урока.

Образовательные:

- научиться использовать алгоритм исследования функций с помощью производной для решения физических задач;

- находить различные способы решения задач;

- выбирать наиболее рациональный способ решения.

Развивающие:

-развить умение обобщать, строить причинно-следственные связи, логически мыслить.

Воспитательные:

-воспитывать трудолюбие, самостоятельность в суждениях, интерес к учению.

Оборудование: мультимедийный проектор, компьютер.

Этапы урока 1.

1. Организационный момент (1минута).

2. Повторение основных вопросов предыдущего урока (10 минут).

3. Постановка цели и задач урока (1минута).

4. Изучение нового материала (30минут)

5. Постановка задачи перед выполнением следующего этапа (3 минуты).

Общие методические замечания.

Главная цель урока - продемонстрировать возможности метода исследования функции на экстремум для нахождения наибольших и наименьших значений функции. В ходе обсуждения, анализируя физическое явление, подвести учащихся к «видению» использования данного метода. Обратить внимание учащихся на возможность использования других методов решения. На этапе «Повторение материала» важно решить задачу №1, используя малые приращения, с тем, чтобы напомнить учащимся физический смысл производной.

В течение урока учащиеся: моделируют физическую ситуацию, устанавливают функциональные зависимости, исследуют полученные выражения, анализируют полученный ответ, осуществляют поиск других способов решения задачи.

Домашнее задание задается по ходу объяснения материала, поскольку подобрано так, что потребует от учащихся обращения к материалу и его повторному осмыслению. Учащиеся I и II варианта получают различные задания. Это сделано не случайно, поскольку ученики «математических» классов любят дискутировать, «сверять» ответ, отстаивать свою точку зрения, а это приучает их самостоятельно анализировать задачи, развивая сознательность и рассуждения.

Конспект урока по теме: Нахождение наибольших и наименьших значений физических величин».

Ход урока.

После сообщения цели урока учитель обосновывает необходимость повторения основного материала предыдущего урока.

Предполагаемый результат: учащиеся мобилизуют резервы памяти, включают внимание.

На этапе повторения, учащиеся вспоминают физический смысл производной, решая задачи №1 и №2. У доски работают двое учащихся.

Задача № 1.

Точка перемещается вдоль оси так, что ее координата изменяется по закону: x(t)=6+0,125t². Найти скорость точки в момент t=2 c. Решить задачу, пользуясь определением скорости в терминах малых приращений и с помощью правил дифференцирования функции.[ 1]

Задача № 2.

Вдоль прямой движется тело, его скорость возрастает по мере удаления от начала координат - она пропорциональна квадрату этого расстояния. В точке с координатой x=5 м скорость V=2м/с. Найти ускорение тела в этой точке. Оформление доски после этапа повторения.[ 2]

Примерное оформление доски после этапа «Повторение материала».

Задача №1

x(t)=6+0,125t²

, устремляя ∆t к нулю, получим

v(2)=0,5 м/с.

Найдем v(t=2) c помощью правил дифференцирования: v′(t=2)=0,25t=0,5 м/с.

Задача № 2.

По условию: v=kx² .

Скорость v(x,t) и x(t), тогда ускорение найдем как производную сложной функции:

Учитывая, что , получим

Окончательно: a=2vkx=2k²x³ (*).

Из начальных условий найдем k: k=2/25=0,08(м.с)^-1, подставим в(*).

Ответ: а=1,6м/с².

Ожидаемый результат: выявлено качество знаний, глубина понимания физического смысла производной, умение логически мыслить, кратко и грамотно строить речь.

Изучение нового материала.

Учитель сообщает учащимся, что на уроках математики они изучили методы, которые позволяют находить наибольшие и наименьшие значения функций. Учитель демонстрирует применение этих знаний на примере следующей задачи.

Задача №1. Необходимо с поверхности земли попасть камнем в цель, которая расположена на высоте h на расстоянии s по горизонтали. При какой наименьшей скорости камня это возможно? Сопротивлением воздуха пренебречь.[ 3]

Учащиеся записывают уравнение движения камня по горизонтали и по вертикали: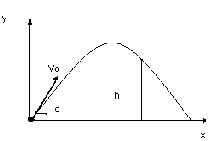

l=Vo (cosα)t;

h= Vo(sinα)t - gt²/2. Исключив время из этих уравнений, получают уравнение траектории камня.

h=ltgα - (gl ² )/2vo²cos²α. (1)

Далее, ставится проблема: уравнение (1) содержит неизвестные Vo и α, и имеет, поэтому, бесчисленное множество решений. Задача - из бесконечного количества траекторий выбрать ту, которая соответствует наименьшему значению Vo.Учитель: «Предположим, что вершина траектории проходит через цель, тогда α=45^о, а скорость наименьшая (демонстрируется траектория камня на экране). Сдвинем мишень влево. Камень, пролетая по выбранной траектории, не попадает в цель, значит надо увеличить скорость. Однако, двигаясь по навесной траектории, камень может попасть в цель, имея прежнюю скорость. Делаем вывод что цель должна находится на нисходящей ветви параболы».

Учащимся хорошо известен алгоритм исследования функции на экстремум. В ходе обсуждения записывается исследуемая функция.

Оформление доски в ходе решения задачи.

(делаем замену в (1):1+ tg²α=1/cos² α)

(2)

Исследуем на экстремум функцию:

,где z=tgα.

f′(z)=gl²/2[(1+z²)′ (lz-h)^-1+(1+z²)((lz-h)^-1)′]

Приравняем производную нулю, получим:

(3)

Найдем значение функции в этой точке:

.

Учитель: «Проанализируем (3), рассмотрев предельные случаи».

1.h=0, tgα=1, α=π/4. Учащимся хорошо известен этот случай максимальной дальности полета по горизонтали, а в случае заданной дальности - это соответствует минимальной скорости Vo_min=(gl)^1/2.

2. 0, ^π/2. Камень надо бросать вверх, только так можно попасть в цель.

Учитель обращает внимание учащихся на то, что чем выше расположена цель, тем больше должна быть начальная скорость камня. Поэтому, вместо того чтобы искать минимум Vo при заданном значении h, можно искать максимум для h при заданном Vo. Найти решение этой задачи, исследуя функцию h(α), предлагается учащимся первого варианта в качестве домашнего задания. Подводя итог обсуждению задачи, учитель обращает внимание учащихся на то, что задачу можно решить и без использования производной, средствами элементарной математики. Это домашнее задание получают учащиеся второго варианта.

Предваряя разбор следующей задачи, учитель обращает внимание на то, что в ней существенную роль играет выбор СО.

Задача №2. Под каким углом α надо тянуть за веревку тяжелый ящик массы m для того, чтобы передвигать его волоком по горизонтальной шероховатой поверхности с наименьшим усилием, если коэффициент трения равен μ? Каково значение этой минимальной силы? [4]

После выполнения анализа и чертежа, учащиеся подводятся к выводу, что сила F будет минимальной, при условии, что ящик движется равномерно. Учащиеся самостоятельно записывают уравнение II закона Ньютона в векторном виде при условии, что равнодействующая всех сил равна нулю: F+N+Fтр+mg=0. Для исследования этого уравнения записывают его в проекциях на горизонтальную и вертикальную оси.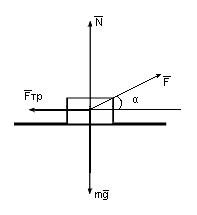

Fcos α -Fтр=0

Fsin α +N-mg=0.

Учитель обращает внимание на то, что сила реакции опоры N и сила трения Fтр тоже зависят от угла α.

Предполагаемый результат: учащиеся объясняют этот факт тем, что если увеличить угол α, то уменьшится величина N, значит уменьшится сила трения, но при этом уменьшится и горизонтальная проекция силы F . Получается, что величина всех сил кроме силы тяжести зависит от угла α. Учащиеся приходят к выводу: чтобы исследовать зависимость силы F от угла α надо исключить N и Fтр из системы уравнений. Учащиеся, учитывая известное соотношение Fтр= μN, получают зависимость F(α).

F(α)=( μmg)/ cos α+ μsin α

Анализируя полученное выражение, учащиеся приходят к выводу, что сила F будет наименьшей, когда знаменатель максимален. По известному алгоритму исследуется на максимум выражение

z(α)= cos α+ μsin α.

z′ (α)=( cos α+ μsin α)′= -sin α+ μcosα

z′ (α)=0

tg α=μ.

Наименьшее значение силы F при этом будет:

Поскольку μcosα=sin α, то

Fнаим.= mgsin α.

Учитель: «Как было замечено вначале, эту задачу можно решить графически».

Учитель сообщает учащимся, что, записывая уравнение II закона Ньютона, имеет смысл оставить в нем полную силу реакции Q, тогда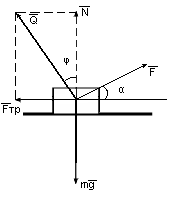

уравнение будет содержать меньшее число слагаемых векторов. Полная сила реакции направлена под некоторым углом φ к поверхности.

F+Q+mg=0, или

Q+mg = - F.

</ Для графического исследования этого уравнения учащимся предлагается найти сумму векторов Q и mg. При выполнении этого задания учащиеся убеждаются, что положение конца вектора не определено. Поскольку вектор F замыкает треугольник сил, то, перебрав различные направления силы F, учащиеся приходят к выводу, что самым коротким вектором будет вектор F, направленный перпендикулярно направлению Q. Приведя геометрические доказательства, учащиеся убеждаются, что вектор F направлен под углом φ к горизонтальной поверхности, а модуль наименьшей силы F =mg sin φ. Подробно этим способом учащиеся будут решать задачу дома.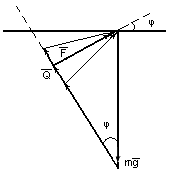

Ожидаемый результат и практическая значимость усвоенных знаний: учащиеся в процессе поисковой беседы анализировали физическое явление, выделяли главное, формулировали задачу на языке математики, использовали алгоритм исследования функции на экстремум, осуществляли выбор наиболее рационального решения; проверяли достоверность ответа предельными переходами; защищали свою точку зрения. Поскольку урок не является контрольным, оценки в ходе урока выставляются по желанию учащихся.

Литература:

1. Турчина Н.В. 3800 задач по физике. М.: Дрофа, 2000.

2. III Соросовская олимпиада 1996-1997. МЦМНО, 1997.

3. Бутиков Е.И., Быков В.,А. Физика в примерах и задачах. М.: Наука, 1983.

4. Бутиков Е.И., Кондратьев А.С. «Механика». М.: Наука, 1994.

7