Методическая разработка урока физики в 7 классе с использованием ключевых учебных ситуаций.

Методическая разработка урока физики в 7 классе с использованием ключевых учебных ситуаций.

1. Выделите две ключевые ситуации в курсе физики 7-го класса.

2. Составьте на основе каждой из этих ключевых ситуаций задачу в трёх уровнях сложности.

3. Опишите методологию решения этих задач с учениками: приведите фрагмент урока.

1. Ключевая ситуация: плотность вещества.

Решение задач на нахождение плотности вещества, массы и объёма тела.

Провожу беседу по вопросам для проверки усвоения материала.

1. Что называют плотностью? (обращаем внимание на то, что плотность характеризует не тело, а вещество, из которого состоит тело).

2. Напишите формулу для определения плотности вещества. ρ = . (проговариваем эту формулу)

3. Какова единица плотности в СИ?

4. Выразить плотность 2,5 в .

5. Как вы думаете, можно ли определить массу вещества, зная его плотность и объём? Напишите формулу для расчёта массы тела по известным плотности и объёму тела. (Да. Определить массу тела по его плотности и объёму можно по формуле m = ρ·V).

6. Как определить объём тела, зная его массу и плотность вещества? Напишите формулу для расчёта объёма тела по известным массе тела и плотности вещества этого тела. (Определить объём тела по его массе и плотности можно по формуле V = )

При решении задач уделяю правильному оформлению условия задачи и её решения.

Решаем задачи на расчёт плотности вещества , массы и объёма тела.

Задача 1. Мальчик нашел кусок металла массой 461,5 г, объём которого 65 см³. Какой это металл?

(После рассмотрения условия задачи приходим к выводу, что вопрос задачи состоит в расчёте плотности вещества и нахождении в таблице плотностей металла с таким (или близким) значением плотности )

Дано: Решение.

m =461,5 г ρ = .

V = 65 см³ ρ = =7,1 = 7100.

ρ - ? В таблице плотности находим, что такое значение плотности

у цинка. Значит, этот металл - цинк.

Ответ: найденный металл - цинк.

Задача 2. Определите массу 0,2 м³ керосина.

Дано: Решение:

V = 0,2 м³ m = ρ·V

ρ_кер =800 . m = 800 · 0,2 м³ = 160 кг.

m - ?

Ответ: m =160 кг.

Задача 3. Какой ёмкости надо взять сосуд, чтобы он вмещал 35 кг бензина?

( Обращаем внимание на то, что вопрос задачи заключается в нахождении объёма жидкости.)

Дано: Решение:

m = 35 кг V =

ρ_бенз =710 . V = ≈ 0, 049 м³.

V - ? 0, 049 м³ = 49 л

Ответ: V = 49 л

Не всегда в задачах даётся значение объёма в явном виде. Поэтому нам необходимо знать и уметь применять формулы объёмов геометрических фигур.

Задача 4. Радиолюбитель поставил антенну из медной проволоки длиной 40 м, площадью поперечного сечения 3,4 мм². Рассчитайте массу медного провода.

Дано: СИ Решение:

ρ_меди =8900 . m = ρ·V

l = 40 м Объём провода рассчитаем по формуле V = S · l

S = 3,4 мм² 0,000 003 4 м² V = 0,000 003 4 м²·40 м =0, 000136 м³

ρ =800 . m = 8900 · 0,000136 м³ = 1,2104 кг.

m - ? Ответ: m =1,2104 кг.

На протяжении многих лет работы обратила внимание на то, что нередко у учащихся возникают проблемы, если в задаче спрашивается: "есть ли в теле полость?". Поэтому не оставляю без внимания решение задач с подобным вопросом. После разбора группы таких задач делаем обобщение результатов.

Задача 5. Чугунная деталь массой 17,6 кг имеет объём 0,004 м³. Найдите плотность чугуна по этим данным. Сделайте вывод, является ли деталь сплошной.

Дано: Решение.

m =17,6 к г ρ = .

V = 0,004 м³ ρ = = 4400 .

ρ - ? В таблице плотности находим, что плотность чугуна 7000 .

при решении задачи получили меньшее значение плотности. Значит, эта деталь содержит пустоты, т. е. полость.

Ответ: деталь не является сплошной.

Вывод. Если в теле есть полость (пустота), то плотность вещества, рассчитанная по массе и объёму тела, будет ............................, чем плотность вещества, указанная в таблице.

Задача 6. Для изготовления алюминиевой детали наружным объёмом 0,005 м³ затрачено 10 кг алюминия. Сколько металла (в кг) должно было быть истрачено, если деталь сплошная? Есть ли в детали полость?

Дано: Решение.

ρ_ал = 2700 m = ρ·V

V = 0,005 м³ m_ал = 2700 · 0,005 м³ = 13,5 кг

m =10 кг Алюминия затрачено меньше, чем для сплошной детали .

m_ал - ? Ответ: m_ал =13,5 кг, в детали есть полость.

Вывод. Если в теле есть полость, то его масса будет ........................., чем масса рассчитанная по табличному значению плотности и измеренному объёму.

Задача 6. Стеклянное тело массой 100 г. имеет объём 50 см³. Каким должен быть объём этого тела, если оно сплошное? Есть ли в теле полость?

Дано: СИ Решение.

ρ_ст =2500 0,1 кг V =

m = 100 г

V = 50 см³ 0,00005 м³ V_ст = = 0, 00004 м³.

V _ст - ? 0, 00004 м³ = 40 см³ - объём сплошного стеклянного тела.

По условию задачи объём стеклянного тела больше, значит, внутри этого тела есть полость. Объём полости можно вычислить.

Ответ: V_спл = 40 см³.

Вывод. Если в теле есть полость, то его объём будет .................. , чем объём, рассчитанный по табличному значению плотности и измеренной массе.

На примере решения этой задачи обсуждаем, как можно вычислить объём полости

V_{полости}= V - V_спл; V_{полости}= 50 см³ - 40 см³= 10см³.

V_{полости}= 10см³.

Подводим итог (можно дать в качестве самостоятельной работы учащимся)

Чтобы определить, есть ли в теле полость, надо :

измерить величины : с помощью приборов:

1. ......................................... 1. .....................................

2. .......................................... 2. .....................................

определить по таблице величину ...........................................

рассчитать величины: 1. ........................... 2. .............................. 3. .............................

по формулам: 1. ............................ 2. .............................. 3. .............................

Определить полость (пустоту) внутри тела ...........................................................................

2. Ключевая ситуация: давление внутри жидкости.

Повторяем вопросы

1) От чего и как зависит давление жидкости на дно сосуда? на стенки сосуда?

2) Одинаковое ли давление оказывает вода на правую и левую стенки сосуда на одной и той же глубине? (рисунок)

3) Почему глубоководные рыбы "взрываются" при быстром поднятии их на поверхность воды?

Разбираем решение экспериментальной задачи. На демонстрационном столе находится аквариум с водой.

Рассчитать: 1) давление воды в аквариуме на его дно; 2) силу давления воды на дно аквариума.

После обсуждения ситуации приходим к выводу: 1)для расчёта давления воды нужно воспользоваться формулой р = ρgh . Для получения ответа необходимо измерить линейкой высоту воды в аквариуме и знать величину плотности воды ρ и ускорение свободного падения g . Затем произвести расчёты.

2) Для расчёта силы давления на дно сосуда необходимо измерить длину a и ширину b основания и рассчитать площадь дна аквариума по формуле S = a ·b . После этого воспользоваться формулой давления р = и из неё выразить силу давления F= p · S. Чтобы получить ответ в ньютонах, не забыть найти площадь в квадратных метрах.

Приучаемся решать тестовые задачи. При этом решения задач оформляем и кратко поясняем.

1. Определите давление в керосине на глубине 25 см.

1. 2000 Па

2. 200 Па

3. 100 Па

2. Определите высоту самой высокой в мире водонапорной башни, если давление воды на стенки труб у её основания равно 411,6 кПа.

1. 41,16 м

2. 45 м

3. 4,116 м

4. 4,5 м

3. Определите силу, с которой керосин действует на квадратную пробку, площадью сечения 16 см², если расстояние пробки до уровня керосина в сосуде равно 40 см.

1. 5,12 Н

2. 512 Н

3. 6,4 Н

4. 64 Н

Рассмотрим решение этих задач подробно (для решения тестовых зада ч предлагается считать ускорение свободного падения g = 9,8 ≈10 )

Задача 1. (решение задачи особых проблем не вызывает, не забываем записать значение плотности керосина из таблицы и высоту столба жидкости выразить в метрах, т.е. в СИ)

Дано: СИ Решение:

ρ_кер =800 . р = ρgh

g = 9,8 . р =800 · 10 · 0,25 м = 2000 Па

h = 25 см 0,25 м

р - ? Ответ: р = 2000 Па

Задача 2. (Задача требует из формулы давления жидкости на дно и стенки сосуда выразить величину высоты столба жидкости. Кроме того, необходимо величину давления выразить в единицах СИ)

Дано: СИ Решение:

ρ_в =1000 . Из формулы р = ρgh выразим высоту h =

g = 9,8 . h =800 = 41,16 м

р = 411,6 кПа 411600 Па

h - ? Ответ: h = 41,16 м.

Задача 3. (В этой задаче необходимо также высоту столба жидкости выразить в метрах. Кроме того, сделать перевод величины площади в СИ, для ответа на вопрос задачи применить формулы расчёта силы давления и давления внутри жидкости.)

Дано: СИ Решение:

ρ_кер =800 . Сила давления на пробку F = p · S

g = 9,8 . Давление керосина на пробку р = ρgh

h = 40 см 0,4 м 1) р =800 · 10 · 0,4 м = 3200 Па

S =16 см² 0,0016 м²

2) F = 3200 Па · 0,0016 м² = 5,12 Н

р - ? Ответ: F =5,12 Н

Если классы достаточно хорошо подготовлены, то можно рассмотреть с ними такую задачу (или даже предложить в качестве домашнего задания!).

В опыте по демонстрации гидростатического давления воды Паскаль использовал трубку длиной 5 метров с площадью поперечного сечения 1 см² и бочку с площадью поверхности 2 м². Какое давление создаст эта вода при вертикальном расположении трубки? С какой силой вода действует на поверхность бочки?

Рассмотреть иллюстрации этого опыта и выдвинуть свои версии объяснения наблюдаемого явления.

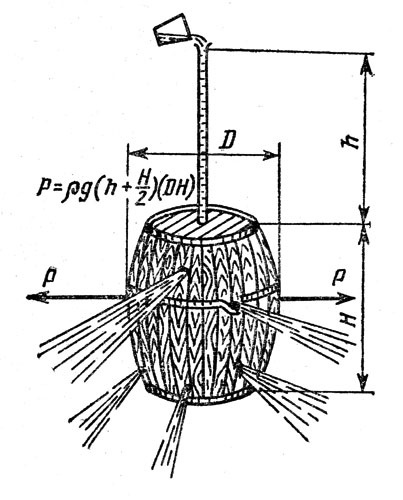
Опыт Паскаля

Предисловие

</ Опыт Торричелли, доказавший существование атмосферного давление и способствовавший созданию ртутного барометра подтолкнул Блеза Паскаля на один интереснейший опыт, названный позже "Бочка Паскаля".



Опыт

По указанию Паскаля, крепкую дубовую бочку до краев наполнили водой и наглухо закрыли крышкой. В небольшое отверстие в крышке вставили конец вертикальной стеклянной трубки такой длины, что конец ее оказался на уровне второго этажа.



Выйдя на балкон, Паскаль принялся наполнять трубку водой. Не успел он вылить и десятка стаканов, как вдруг, к изумлению обступивших бочку зевак, бочка с треском лопнула. Ее разорвала непонятная сила. Паскаль убеждается: да, сила, разорвавшая бочку, вовсе не зависит от количества воды в трубке. Все дело в высоте, до которой трубка была заполнена.



Далее проявляется удивительное свойство воды - передавать давление, создаваемое на ее поверхности (в бочке) по всему объему, каждой точке стенки или дна бочки. Так он приходит к открытию закона, получившего его имя.