- Учителю
- Конспекты уроков по физике 9 класс
Конспекты уроков по физике 9 класс
Физика 9 Амирова Н.Г.
Урок 1.
Материальная точка. Система отсчета. Вводный инструктаж по Т.Б.
Цели урока:
Объяснить необходимость изучения механики. Показать возможности ее практического применения. Сформировать у учащихся представление о материальной точке.
Ход урока
I. Вступление
Во вступительной части учитель рассказывает, что будут изучать учащиеся в этом учебном году, какие задания их ждут. Так же необходимо напомнить технику безопасности на уроках физики и во время проведения лабораторных работ.
Далее необходимо вспомнить, что такое физика.
Физика - это наука, занимающаяся изучением самых общих свойств окружающего нас материального мира.
Физика - наука экспериментальная, ее цели, во-первых, отыскать наиболее общие законы природы, во-вторых, объяснить конкретные процессы действием этих общих (фундаментальных) законов. В то же время физика и количественная наука. Все основные законы физики формируются на математическом языке. И этот язык надо знать, а он не прост.
Основные разделы физики:
♦ Механика
♦ Термодинамика
♦ Электродинамика
II. Новый материал
Механика, к изучению основ которой мы приступаем, - это наука о движении и взаимодействии макроскопических (от греческого слова makros - большой, длинный) тел. Название «механика» происходит от греческого слова mechanike, что означает наука о машинах, искусство постройки машин. Первые простейшие машины (рычаг, клин, колесо, наклонная плоскость и т. д.), которые теперь называют простыми механизмами, появились в древности. Первое орудие человека - палка - это рычаг. Каменный топор - сочетание рычага и клина. Колесо появилось в бронзовом веке, позже стали применять наклонную плоскость.
Уже в V в. до н. э. в афинской армии применялись стенобитные машины - тараны, метательные приспособления - баллисты и катапульты. Строительство плотин, мостов, пирамид, а также ремесленное производство, с одной стороны, способствовали накоплению знанию о механических явлениях, а с другой стороны, - требовали от них новых знаний. В ответ на запросы практики в новых знаниях и возникла наука механика.
Первые дошедшие до нас сочинения по механике, в которых описаны простейшие машины, принадлежат ученым Древней Греции. К ним относится сочинение «Физика» Аристотеля (IV в. до н. э.), в котором впервые введен в науку термин «механика». В III в. до н.э. древнегреческий ученый Архимед впервые применил математику для анализа и описания механических явлений. Архимед сформулировал закон равновесия рычага и закон плавания тел. С этого времени начинается развитие механики как науки.
Новый этап связан с работой Г. Галилея, сформулирован закон инерции, установил законы падения тел и колебаний маятника. Английский физик И. Ньютон, опираясь на работы Галилея и его современников, а так же на результаты своих собственных исследований, создал цельное учение о механическом движении и взаимодействии тел, которое получило название классической механики. Классическая механика состоит из трех частей: кинематика, динамика, статика.
Слово кинематика происходит от греческого слова kinematos - движение. Кинематика изучает, как движется тело, но не изучает, почему тело движется так, а не иначе. Основными задачами кинематики являются:
а) Описание с помощью математических формул, графиков или таблиц совершаемых телом движений.
б) Определение кинематических величин, характеризующих это движение.
Для описания движения в кинематике вводятся специальные понятия (материальная точка, система отсчета, траектория) и величины (путь, перемещение, скорость, ускорение), которые важны не только в кинематике, но и в других разделах физики.
Первое, что бросается в глаза при наблюдении окружающего мира, - это его изменчивость.
- Какие изменения вы замечаете? (Ночь меняет день, вода при охлаждении замерзает, падают капли, лает собака, едет автомобиль, двигаются литься деревьев в ветреную погоду.)
- Поведем итог: наиболее частые ответы связаны с изменением положения тел относительно друг друга.
Изменение положения тела в пространстве относительно других тел с течением времени называются механическим движением.
Однако одно и то же тело одновременно может и двигаться и не двигаться, если наблюдать его с различных точек зрения.
Пример 1. В купе вагона на столике лежит яблоко. Пассажир видит, что расстояние до яблока с течением времени сохраняется. Яблоко не совершает механического движения. Но с точки зрения провожающего, яблоко движется, т.к. расстояние от яблока до перрона с течением времени растет.
Пример 2. Вы находитесь в классе в покое (сидя за партой) относительно Земли, но движетесь вместе с Землей вокруг Солнца.
Из этих примеров следует: нет, и не может быть абсолютно неподвижных тел.
Даже самое простое движение тела оказывается сложным для изучения. Для того чтобы облегчить исследования, вводят ряд упрощений. Если мы рассматриваем движение автомобиля, длина которого 5 м, прошедшего 100 км, то пройденное им расстояние в 200000 раз больше его собственной длины. Очевидно, что автомобиль можно рассмотреть как точку. В этом случае пользуются термином материальная точка. Но если мы будем исследовать силу сопротивления воздуха, действующего на движущийся автомобиль, считать его материальной точкой нельзя, т. к. сила сопротивления зависит от размеров автомобиля. Материальная точка - это абстрактное понятие, введенное для упрощения изучения многих физических явлений.
Материальной точкой называют тело, размерами и формой которого в рассматриваемом случае можно пренебречь.
- Как же определить положение тела (материальной точки)?
В одном древнем документе, относящемуся к началу нашей эры, сказано: «Стань у восточной стены крайнего дома лицом на север, и, пройдя 120 шагов, повернись лицом на восток. Затем, пройдя 200 шагов, вырой яму в 10 локтей и найдешь 100 золотых монет».
- Если бы этот документ попал в Ваши руки, смогли бы найти клад? (У каждого человека разные шаги и локти. Не указан населенный пункт. Местность сильно изменилась. Нет дома, от которого нужно считать.)
Итак, необходимо тело отсчета. Если через него провести оси координат, то положение тела в пространстве можно задать его координатами. Но при движении тела его положение меняется с течением времени. Значит, нужен прибор для измерения времени (часы), связанные с телом отсчета.
Все вместе: а) тело отсчета, б) система координат, в) прибор для определения времени, - образуют систему отсчета.
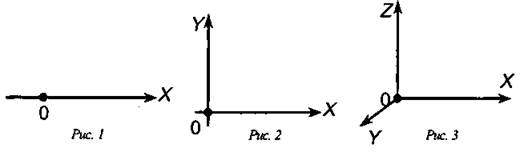
Система отсчета может быть: а) одномерной, когда положение тела определяется одной координатой (рис. 1); б) двухмерной, если положение тела определяется двумя координатами (рис. 2); в) трехмерной, т.е. положение тела определяется тремя координатами (рис. 3).
III. Упражнения и вопросы для повторения
- В каких из перечисленных случаев можно считать тела материальными точками, а в каких - нельзя?
1. На станке изготавливают спортивный диск. (Не материальная точка.)
2. Тот же диск после броска спортсмена летит на расстояние 55 м. (Материальная точка.)
3. Конькобежец проходит дистанцию соревнования. (Материальная точка, но не всегда: не надо забывать про фотофиниш.)
4. Фигурист выполняет упражнения произвольной программы. (Не материальная точка.)
5. За движением космического корабля следят из Центра управления полетов на Земле. (Материальная точка.)
6. За тем же кораблем наблюдает космонавт, осуществляющий с ним стыковку. (Нематериальная точка.)
7. Земля вращается вокруг своей оси. (Нематериальная точка.)
8. Земля движется по круговой орбите вокруг Солнца. (Материальная точка.)
Домашнее задание
1. Выучить материал § 1, записи в тетради;
2. Упражнение 1 (учебник, стр. 9);
3. Материал для повторения математики:
а) Из формулы v = at выразите а через v и t; t через а и v.
б) Из формулы v=v0 + at выразите v0, a, t.
Урок 2.
Перемещение. Определение координаты движущегося тела.
Цели урока:
Ввести понятия «перемещение», «путь», «траектория». Научить определять координаты движущегося тела.
Ход урока
I. Повторение. Проверка домашнего задания
Перед уроком учащиеся выписывают на доске домашнее задание:
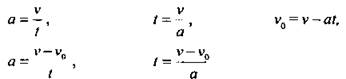
Упражнение 1 проверяется устно.
Один ученик вызывается к доске и пересказывает параграф.
Нескольким ученикам раздаются карточки с индивидуальными заданиями, которые выполняются во время устного ответа.
Карточка 1
а) Какую систему координат (одномерную, двухмерную или трехмерную) следует выбрать для определения положения тел:
♦ трактор в поле (двухмерная);
♦ вертолет (трехмерная)',
♦ поезд (одномерная)',
♦ шахматная фигура (двухмерная).
б) Дано выражение: ![]() Выразите: a, v0.
Выразите: a, v0.
(Ответ: ![]() )
)
Карточка 2
а) Какую систему координат (одномерную, двухмерную или трехмерную) следует выбрать для определения положения таких тел:
♦ Люстра в комнате (двухмерная);
♦ Лифт (одномерная);
♦ Подводная лодка (трехмерная);
♦ Самолет на взлетной полосе (одномерная).
б) Дано выражение: ![]() Выразите: v2,
v02, а.
Выразите: v2,
v02, а.
(Ответ: ![]() )
)
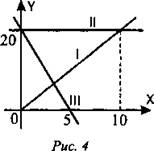
в) Даны графики (рис. 4). Записать для каждого из них формулы соответствующих им функций.
(Ответ: I. у = 2х; II. y = 20; III. y = 20 - 4x.)
II. Перемещение тела. Траектория
С изменениями координат связана первая из величин, вводимых для описания движения, - перемещение.
Перемещением тела (материальной точки) - называется вектор, соединяющий начальное положение тела с его последующим положением.
Перемещение принято обозначать буквой ![]() . В СИ перемещение
измеряется в метрах (м).
. В СИ перемещение
измеряется в метрах (м).
Перемещение - величина векторная, т. е. кроме числового значения
имеет еще и направление. Векторную величину изображают в виде
отрезка, который начинается в некоторой точке и заканчивается
острием, указывающим направление. Такой отрезок - стрелка -
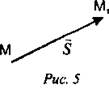
называется вектором. Например, перемещение ![]() - вектор, проведенный
из точки М в точку M1(рис. 5).
- вектор, проведенный
из точки М в точку M1(рис. 5).
Знать вектор перемещения - значит, знать его направление и модуль. Модуль вектора это скаляр, т. е. численное значение. Зная начальное положение и вектор перемещения тела, можно однозначно определить, где находится тело.
Следует всегда различать понятия пути и перемещения. Путь - величина скалярная. Перемещение - векторная.
Для того чтобы ввести определения пути, необходимо еще одно понятие - траектория.
Непрерывную линию, которую описывает движущееся тело (рассматриваемое как материальная точка) по отношению к выбранной системе отсчета, называют траекторией (рис. 6).
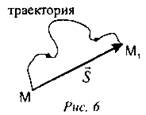
Траектория может быть известна еще до начала движения. Так, полотно железной дороги определяет траекторию поездов. Заранее рассчитывается траектория движения искусственных спутников Земли.
В зависимости от траектории движения могут быть прямолинейными (падение тел в опыте Галилея) и криволинейными (движение брошенного под углом к горизонту мяча).
Траектория одного и того же движения различна в разных системах отсчета.
Например, для пассажира равномерно двигающегося поезда падающий в вагоне мячик двигается вертикально вниз, а для человека, стоящего на перроне, тот же мячик двигается по параболической траектории.
Длина траектории - путь. Модуль перемещения и путь могут совпадать по значению, только в том случае, если тело движется вдоль прямой в одном направлении.
III. Проекция вектора на ось
Важным понятием является понятие проекции вектора (рис. 7).
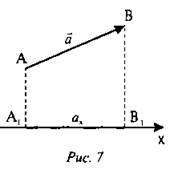
Опустим из точек А и В (начало вектора и его конец) перпендикуляры на ось ОХ. Длину отрезка A1B1, взятую со знаком «+» или «-» называют проекцией вектора на ось ОХ. Проекция вектора - величина скалярная.
Проекцию считают положительной (ах > 0), если от проекции начала вектора к проекции его конца нужно идти по направлению оси.
Другими словами, проекция вектора положительна, если угол между направлением вектора и осью ОХ острый.
В противном случае проекция вектора отрицательна (аx < 0).
Если вектор перпендикулярен оси, то при любом направлении вектора его проекция на ось равна нулю (ах = 0).
IV. Упражнения и вопросы для повторения
- Путь или перемещение мы оплачиваем при поездке в такси? (Путь.)
- Мяч упал с высоты 3 м, отскочил от пола и был пойман на высоте 1 м. Найти путь и перемещение мяча. (Путь 4 м, перемещение 2 м.)
- Велосипедист движется по окружности с радиусом 30 м. Чему равны путь и перемещение велосипедиста за половину оборота? За полный оборот? {Пройденный за пол оборота путь равен l = пR = 94,2 м, перемещение S = 2R= 60 м. За один оборот путь l = 2πR = 188,4 м, перемещение S2 = 0.)
Домашнее задание
1. § 2, 3. Ответить на вопросы в конце параграфа;
2. Выполнить упражнение 3 (учебник);
Урок 3.
Перемещение при прямолинейном равномерном движении.
Цели урока:
Ввести понятие скорости как векторной величины. Научить описывать движение различными способами: графическим и координатным (как функцию от времени).
Ход урока
I. Повторение. Проверка домашнего задания
Повторение изученного можно провести в виде фронтального опроса либо проверочной самостоятельной работы по изученному материалу. Фронтальная беседа
- В чем состоит основная задача механики?
- Зачем введено понятие материальной точки? Когда тело можно считать материальной точкой? Приведите примеры.
- Что такое система отсчета? Для чего она вводится?
- Какие виды систем координат вы знаете?
- Какую систему координат вы выберите для определения положения таких тел: стрекоза в полете, шахматная фигура на доске, теплоход движется на реке, лифт в доме, пуговица на одежде?
- Что такое траектория, путь, перемещение?
- В чем отличие пути от перемещения?
- В каком случае путь равен траектории? Приведите примеры.
- Подбросьте тело вверх и поймайте его при спуске. Что больше: путь тела или перемещение?
- Как определить проекцию вектора? (правило)
- Как определить проекцию вектора перемещения на ось?
Во время беседы на доске проверяется решение домашних задач.
Задания для самостоятельной работы:
Вариант I
1. Мяч падает с высоты 2 м, и, отскочив от земли, поднимается на высоту 1,5 м. Чему равны путь l и модуль перемещения S мяча? (Ответ: l = 3,5 м, S = 0,5 м.)
2. Материальная точка движется по окружности радиуса R. Чему равны путь l и модуль перемещения S через пол-оборота? (Ответ: l = πR, S = 2R.)
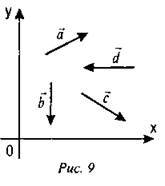
3. Укажите знаки проекций векторов на оси ОХ, ОY (рис. 9).
Вариант II
1. Мяч упал с высоты 4 м от пола и был пойман на высоте 2 м. Найти путь lи модуль перемещения S мяча. (Ответ: l = 6 м, S = 2 м.)
2. Автомобиль двигался по кольцевой дороге вокруг Москвы и дважды по ней проехал. Чему равны путь l и перемещение S, если длина кольцевой дороги L? (Ответ: путь l = 2L, перемещение S = 0.)
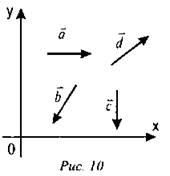
3. Укажите знаки проекций векторов на оси ОХ, OY (рис. 10).
II. Новый материал
Эксперимент I
На демонстрационном столе стоит стеклянная трубка, наполненная водой. При быстром се перевертывании пузырек воздуха начинает всплывать (можно открыть трубку и погрузить в жидкость какое-либо сферическое тело). Отмечая положения пузырька через равные промежутки времени (через 2 с), получаем таблицу:Из опыта видно, что за одинаковые промежутки времени тело перемещается на одно и то же расстояние. Это пример равномерного движения. Движение пассажира на эскалаторе в метро, движение конвейерной ленты, спуск парашютиста в безветренную погоду - это все примеры равномерного движения.
Движение тела называется равномерным, если за любые равные промежутки времени тело перемещается на одинаковое расстояние (т. е. проходит одинаковые пути).
Как найти (вычислить) перемещение тела за какой-то промежуток
времени t? Для этого надо знать перемещение тела за единицу
времени. Это отношение называют скоростью и обозначают буквой
![]() :
:
![]()
где ![]() -
скорость [м/с],
-
скорость [м/с], ![]() - перемещение [м], t - время
[с].
- перемещение [м], t - время
[с].
Направлен вектор скорости так же, как и вектор перемещения. Направление вектора скорости - это и есть направление движения тела.
При вычислении перемещения и скорости обычно пользуются формулами, в которые входят не векторы, а проекции векторов:
![]()
Следовательно:
![]()
Таким образом:
![]()
где х - конечная координата [м],
х0- начальная координата [м],
vx - проекция скорости на ось ОХ,
t - время [с].
Мы нашли зависимость координаты x от времени t, т. е. х(t).
Данная зависимость линейная. Из математики известно, что графиком линейной функции у = kx + b является прямая.
Далее можно рассмотреть различные варианты графиков зависимости координаты х от времени (при vx = 0, vx > 0, vx < 0).
Теперь построим график vx(t) - график зависимости скорости от времени (см. рис. 11).
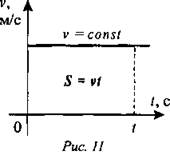
По графику скорости можно найти путь. Численно он будет равен площади заштрихованной фигуры (в данном случае прямоугольник) за время t, т. е. S= vt.
III. Упражнения и вопросы для повторения
1. Определите по рис. 12 начальные координаты бензоколонки (А), грузового (В) и легкового (С) автомобилей и мотоцикла (D). Запишите уравнение зависимости координаты от времени для каждого тела. Определите координаты тел через 1,5 ч.
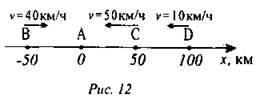
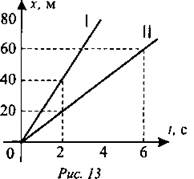
2. По графикам изменения координат двух тел (рис. 13) сравнить их скорости. Записать уравнение x(t). Построить vx(t) и найти путь за 2 с. Сделать рисунок, на котором указать положение тел (ось ОХ направить вправо).
Домашнее задание
1. Выучить материал § 4;
2. Ответить на вопросы в конце параграфа;
3. Выполнить упражнение 4 (стр. 20)
Урок 4.
Прямолинейное равноускоренное движение. Ускорение
Образовательные:
-
сформировать понятие прямолинейного равноускоренного движения, ускорения; рассмотреть основные характеристики равноускоренного движения;
-
построить графики скорости равномерного и равнопеременного движения;
-
продолжить формирование знаний по физическим основам получения переменного тока.
Развивающие:
-
развивать практические умения учащихся: умение анализировать, обобщать, выделять главную мысль из рассказа учителя и делать выводы;
-
развивать умение применять полученные знания в новых условиях.
Воспитывающие:
-
расширить кругозор учащихся о видах механического движения (в частности, о прямолинейном равнопеременном (равноускоренном) движении);
-
отрабатывать навыки учебного труда по составлению опорного конспекта (схемы) материала.
Тип урока
изучение и первичное закрепление новых знаний
Формы работы на уроке
Эвристическая беседа, составление опорного конспекта (схемы), наблюдение, фронтальная работа, работа в группах, индивидуальный опрос (работа в тетрадях, рефлексия)
Методы обучения
Проблемно-поисковый, репродуктивный
Средства обучения
- учебник "Физика-9" (Пёрышкин, Гутник), рабочие тетради, цветные мелки, бланки для рефлексии;
- компьютер, проектор, экран;
- флеш-анимации
- OMS-модули «Траектория, путь и перемещение», «Ускорение» (интерактивные и демонстрационная модели)
Демонстрации
«График скорости равномерного движения» и «Определение пути равнопеременного движения по графику скорости»
«Ускорение автомобилей», «Равнопеременное движение», «Равноускоренное движение тела»
«Равнопеременное (равноускоренное) движение»
Этапы урока
Оргмомент
Установление готовности класса к уроку.
Мотивация
Ребята (3-4 человека), подойдите по очереди к доске и нарисуйте цветными мелками на этой импровизированной карте села свой путь от дома до школы (остальные в тетрадях рисуют свои маршруты)…
Посмотрите, сколько разных линий получилось. И по форме, и по длине. Что мы можем определить по данным рисункам?.. OMS-модуль «Траектория, путь и перемещение»
А теперь подпишите над своими дорогами приближённое количество затраченного времени и примерное расстояние. Рассчитайте свою скорость. И вспомните, вы по пути не останавливались? ни за кем не заходили? никого не догоняли?.. Да, у многих из вас скорость имела по несколько разных значений. А можете вы сказать, как быстро вы увеличивали или уменьшали свою скорость?.. Обратимся к науке. Какой раздел механики нам может помочь в вопросах, связанных с описанием движения?
Актуализация знаний
Кинематика
Кинематика - (от греч. kinematos - движение), раздел механики, в
котором изучаются геометрические свойства движения тел без учета их
массы и действующих на них сил. Напомните, пожалуйста, основные
характеристики движения…
Итак, что изучает кинематика?
Виды движения:
Прямолинейное:
-
Равномерное
-
Неравномерное (равноускоренное и с переменным ускорением)
Криволинейное:
-
Равномерное движение по окружности
-
Ускоренное движение по окружности
Вращательное:
-
Равномерное вращение
-
Вращение с ускорением
Колебательное:
-
Гармонические колебания
-
Негармонические колебания
Изучение нового материала
При неравномерном движении мгновенная скорость тела непрерывно
изменяется: от точки к точке, от одного момента времени к другому.
Как же вычислить скорость в любой момент времени?
Для этого нужно знать, как быстро изменяется скорость, или, другими
словами, каково ее изменение в единицу времени.
Для простоты мы будем рассматривать такое неравномерное движение
тела, при котором его скорость за любые равные промежутки времени
изменяется одинаково. Такое движение называется
равноускоренным.
Движение, при котором скорость за любые равные промежутки времени
изменяется одинаково, называют равноускоренным движением.
Если в некоторый начальный момент времени скорость тела равна
![]() , а через
промежуток времени t она оказывается равной
, а через
промежуток времени t она оказывается равной ![]() , то за каждую единицу
времени скорость изменяется на
, то за каждую единицу
времени скорость изменяется на ![]()
Величина ![]() характеризует быстроту
изменения скорости. Ее называют ускорением и обозначают буквой
характеризует быстроту
изменения скорости. Ее называют ускорением и обозначают буквой
![]() :
:
![]() (1)
(1)
Ускорением движущегося тела называют величину, равную отношению
изменения скорости тела к промежутку времени, в течение которого
это изменение произошло.
Если ускорение тела по абсолютному значению велико, то это значит,
что оно быстро набирает скорость (когда тело разгоняется), или
быстро теряет ее (при торможении).
Если ускорение ![]() известно, то можно вычислить
значение скорости
известно, то можно вычислить
значение скорости ![]() тела в любой момент времени,
если известно еще и значение начальной скорости
тела в любой момент времени,
если известно еще и значение начальной скорости ![]() .
.
Действительно, из формулы (1) следует, что ![]()
Ускорение и нужно знать для вычисления скорости ![]() .
.
Так как ускорение равно произведению векторной величины ![]() на скаляр
на скаляр ![]() , оно само является
векторной величиной.
, оно само является
векторной величиной.
В каких единицах измеряют ускорение?
Так как ![]() ,
то абсолютное значение ускорения равно единице, если равно единице
абсолютное значение изменения скорости и равен единице промежуток
времени.
,
то абсолютное значение ускорения равно единице, если равно единице
абсолютное значение изменения скорости и равен единице промежуток
времени.
За единицу ускорения принимают ускорение такого движения, при
котором за единицу времени скорость изменяется на единицу
скорости.
В системе единиц СИ скорость измеряется в метрах в секунду, а время
- в секундах, так что ускорение измеряется в метрах в секунду за
секунду или в метрах на секунду в квадрате м/с2.
Усвоение нового материала
OMS-модуль «Ускорение»:
Интерактивные модели «Ускорение автомобилей», «Равнопеременное движение», «Равноускоренное движение тела»
Демонстрационная модель «Равнопеременное (равноускоренное) движение»
Вопросы к уроку
Конспект
Домашнее задание
конкурс опорных конспектов урока, § 5, упр.5;
+ сообщение-доклад по теме;
+ исследовательский мини-эксперимент «Семейное движение» (определить вид механического движения каждого члена семьи во время перемещения по домашним делам, например, за стол обедать, вынести мусор, идти спать и т.д., можно и с домашними питомцами);
+ рассчитать своё ускорение на каком-либо участке пути.
Рефлексия
- Заполните, пожалуйста, бланк «выходного» билета, полное заполнение которого даст вам возможность покинуть кабинет сразу после звонка с урока:
Пожелания и предл
жения
- Спасибо за работу на уроке, ребята!
Пример 1
Автомобиль, движущийся со скоростью 10 м/с, начал тормозить с ускорением 1 м/с2. Сколько времени пройдет до остановки автомобиля?
Дано:
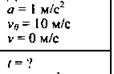
Решение:
Запишем уравнение для скорости при равноускоренном движении в проекциях на ось ОХ:
![]()
Т. к. векторы скорости и ускорения направлены в противоположные стороны, то их проекции имеют разные знаки. Получаем уравнение: v = v0 -at.
Отсюда: ![]()
Ответ: t = 10 с.
Пример 2
Тело движется прямолинейно с уменьшающейся скоростью. Ускорение равно 4 м/с2. В некоторый момент времени модуль скорости тела v0 = 20 м/с. Найдите скорость тела через t1 = 4 c и t2, = 8 c после этого момента. Определите также момент времени, когда тело останавливается.
Дано:
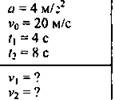
Решение:
![]()
Т. к. векторы скорости и ускорения направлены в противоположные стороны, то в проекциях на ось ОХ получаем уравнения: v1x = v0 - at1, v2x =v0 - at2.
![]()
Знак минус у проекции скорости означает, что к исходу 8-ой секунды тело двигалось в направлении, противоположном направлению начальной скорости. Модуль скорости v2 = ? v2X? = 12 м/с.
Можно вычислить момент, когда тело остановилось, т. е. когда v3 = 0:
![]()
Ответ: v1 = 4 м/с; v2 = -12 м/с, t = 5 с (время остановки тела).
Урок 5.
Скорость прямолинейного равноускоренного движения.
Цели урока:
Научиться строить график скорости от времени. Сформировать понятия перемещения при прямолинейном равноускоренном движении. Научиться его находить.
Ход урока
I. Повторение. Проверка домашнего задания
- Дайте определение мгновенной скорости.
- Каков физический смысл мгновенной скорости?
- Что такое ускорение?
- Назовите единицы ускорения.
- Как рассчитывается мгновенная скорость при равноускоренном движении?
- Чем отличаются векторные величины от скалярных?
- Что показывает модуль вектора ускорения?
- Каковы правила сложения векторных величин?
С целью повторения материала можно предложить учащимся ряд простых устных задач по изученной теме:
1. Какой путь пройдет велосипедист за 2 ч, если его средняя скорость 15 км/ч?
2. Чему равна мгновенная скорость камня, брошенного вертикально вверх, в верхней точке траектории?
3. О какой скорости - средней или мгновенной - идет речь в следующих случаях:
а) пуля вылетает из винтовки со скоростью 800 м/с;
б) самолет летит из Киева в Москву со скоростью 800 км/ч;
в) скоростемер на тепловозе показывает 75 км/ч?
II. Скорость при равноускоренном движении
Задание 1
На рис. 17 показаны тела, их скорости и ускорения. Запишите уравнения скорости для каждого тела и определите скорость через 5 с после начала движения.
1) v1 = 2t; через 5 с: v = 10 м/с;
2) v2 = 8 + 2t; через 5 с: v = 8 м/с + 5 с · 2 = 18 м/с;
3) v3 = 8t; через 5 с: v = 8 м/с - 5 с · 2 = 2 м/с;
4) v4X = - 8 - 2t; через 5 с: v4X = - 8 м/с - 2 · 5 с = - 18 м/с; Модуль скорости v4 = |v4X| = 18 м/с;
5) v5 = 1; через 2 с: v = 1 м/с.
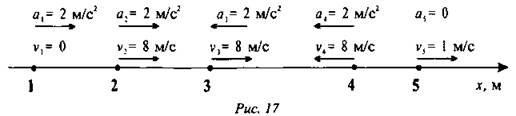
- Постройте график зависимости vx от t для пятого тела. Что будет графиком функции? (Прямая, параллельная оси t.)
- А что будет графиком зависимости для остальных четырех тел? (Прямая.) В данном случае имеем линейную зависимость.
Учитель строит возможные варианты графиков и комментирует их (рис. 18).
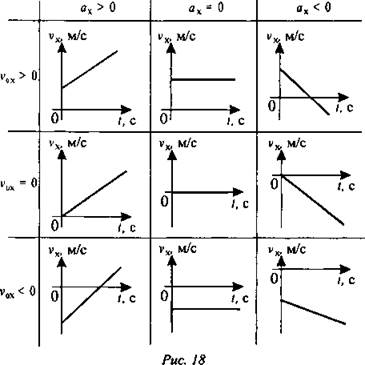
По графику зависимости скорости от времени можно найти ускорение:
![]()
Задание 2
Записать уравнение скорости от времени vx(t) для каждого участка графика (рис. 19).
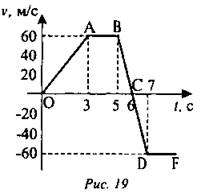
а) Участок ОА: ![]() Уравнение: v = 20t.
Уравнение: v = 20t.
б) Участок АВ: а = 0, v = v0 = 60. Уравнение: v = 60.
в) Далее можно рассматривать участок ВС, а можно сразу BD, т. к. ускорение одинаково на всем участке.
Участок BD: v![]()
Уравнение: v = 60 - 60t
г) Участок DF: a = 0, v = v0 = -60. Уравнение: v = -60.
III. Перемещение при равноускоренном движении
Пусть некоторое тело движется по направлению оси х, имея начальную скорость v0, увеличивая ее до v. Построим график зависимости скорости от времени (рис. 20).
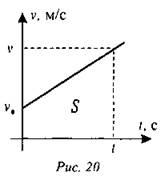
- Как найти перемещение тела?
Вспомним, что площадь, ограниченная графиком скорости, при равномерном движении и осью t, равна пути, пройденному телом.
Путь и перемещение совпадают, если тело движется поступательно вдоль прямой. У нас на графике как раз такой случай, значит, чтобы найти перемещение нужно найти площадь заштрихованной фигуры (трапеции). Площадь трапеции равна:
![]()
где а, b - основания трапеции,
h - высота трапеции.
В нашем случае: a = v0, b = v, h = t.
![]()
Проекция перемещения находится по формуле:
![]()
Тогда для координаты имеем:
![]()
Домашнее задание
1. Выучить § 6 .
2. Выполнить упражнение 7.
3. Ответить на вопрос микротеста:
Уравнение зависимости проекции скорости тела от времени имеет вид: vx= 2 + 3t (м/с). Каково соответствующее уравнение проекции перемещения тела?
![]()
Урок 6
Перемещение при прямолинейном равноускоренном движении.
Цели урока:
-
В целях формирования научного мировоззрения, познакомить учащихся с таким понятием как прямолинейное равноускоренное движение.
-
развить умение мобилизоваться и применять все имеющиеся знания при самостоятельном решении задач; развивать логическое мышление; развивать умения формулировать четкие, лаконичные ответы на вопросы; развивать способности к анализу и синтезу, развивать умения выделять главное, делать выводы, выделять существенные признаки объектов.
-
повторить, обобщить и закрепить знания основных понятий, терминов, формул по теме прямолинейное равноускоренное движение. ознакомить учащихся с выводом формулы проекции вектора перемещения для прямолинейного равноускоренного движения
Формы работы учащихся: фронтальная и индивидуальная
Средства: компьютер, мультимедийный проектор, доска, учебник, журнал
Методы: словесный, практический, объяснительно- иллюстративныйФормы, методы обучения
Средства обучения
(источники информации, ТСО, ЭВТ.)
Время
Организационный (приветствие, выявление отсутствующих, проверка готовности учащихся к уроку, готовность средств обучения…)
фронтальная
Слово учителя, журнал
2-3 мин
Актуализация знаний
Индивидуальная, фронтальная,
метод практический, словесный.
Слово учителя, карточки, фронтальный опрос
12 мин
Изучение нового материала
Фронтальная. Индивидуальная
Метод словесный. Иллюстративный
презентация, ПК, видео- фрагмент.
12 мин
Закрепление нового учебного материала (решение задач)
+ контроль.
Метод практический, словесный
Задачник, учебник.
12 мин
Подведение итогов занятия
Фронтальная
Словесный метод
Слово учителя
2 мин
Ход урока.
Орг. Момент
Приветствие учащихся. Знакомство с ними. Запись в классный журнал отсутствующих учеников. Сообщение темы урока. Запись ее на доске и в тетрадях учащихся.
Актуализация знаний.
Перед тем как мы продолжим изучение данного материала, давайте вспомним и повторим ранее изученное.
-
Какое движение называют равномерным, прямолинейным?
-
Что называют скоростью равномерного движения?
-
В каких единицах измеряют скорость?
-
Как перевести скорость из км/ч в м/с.
-
В каких случаях проекция скорости равномерного движения на ось положительна, в каких отрицательна?
Слушаю ответы учащихся. Затем предлагаю учащимся выполнение небольшой самостоятельной работы на карточках.
Карточка № 1
-
Используя график зависимости скорости движения тела от времени, определите скорость тела в конце 5-ой секунды, считая, что характер движения тела не изменяется
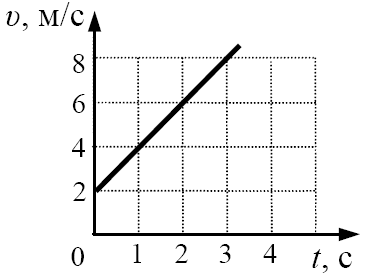
-
9 м/с
-
10 м/с
-
12 м/с
-
14 м/с
-
В течение 30 секунд поезд двигался равномерно со скоростью 54 км/ч. Какой путь он прошел за это время?
Карточка №2.
-
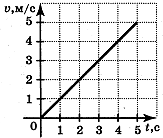 По графику скорости,
изображенному на рисунке, определите путь, пройденный телом за
5 с.
По графику скорости,
изображенному на рисунке, определите путь, пройденный телом за
5 с.
1) 25м
2) 5 м
3)7,5 м
4) 12,5 м
-
При равномерном движении пешеход за 6 секунд проходит путь 12 метров, какой путь он пройдет при движении с той же скоростью за 3 секунды?
Изучение нового материала
Нам необходимо вывести формулу, с помощью которой мы могли бы рассчитывать проекцию вектора перемещения тела, движущегося прямолинейно и равноускоренно, за любой промежуток времени. Для этого обратимся к рисунку 14 на стр 29 вашего учебника. Как на рисунке 14а, так и на рисунке 14б, отрезок АС представляет собой график проекции вектора скорости тела, движущегося с постоянным ускорением а.
Вопрос к классу: по какой формуле при прямолинейном равномерном движении тела определяется вектор перемещения, совершенного над этим телом? (по той же формуле, что и площадь прямоугольника, заключенного под графиком проекции вектора скорости.
Какой вывод мы можем сделать? ( проекция вектора перемещения численно равна площади этого прямоугольника).
Докажем, что и в случае прямолинейного равноускоренного движения проекцию вектора перемещения можно определить по той же формуле, что и площадь фигуры, заключенной между графиком АС, осью Оt и отрезками ОА и ВС. Т.е. что и в этом случае проекция вектора перемещения численно равна площади фигуры под графиком скорости. Для этого на оси Ot (рис 14а) выделим маленький промежуток времени db. Из точек d и b проведем перпендикуляры к оси Ot до их пересечения с графиком проекции вектора скорости в точках a и c.
Таким образом, за промежуток времени,
соответствующий отрезку db, скорость тела меняется от ![]()
![]() .
.
За достаточно малый промежуток времени проекция вектора скорости меняется очень незначительно, поэтому движение тела в течение этого промежутка времени мало отличается от равномерного, т.е. от движения с постоянной скоростью.
В этом случае участок ас графика можно считать горизонтальной, а полоску acbd прямоугольником. Значит площадь этой полоски численно равна проекции вектора перемещения за промежуток времени, соответствующий отрезку db.
На такие полоски можно разбить всю площадь фигуры OACB, которая какой является фигурой?
Следовательно, чему будет равна проекция вектора перемещения за промежуток времени, соответствующий отрезку ОВ? (площади трапеции, и определяется по той же формуле что и эта площадь).
Чему равна площадь трапеции?
Из рисунка 14б найдем основания и высоты трапеции. Назовите их.
АО=![]() ,
ВС=
,
ВС=![]() , ОВ=t ,
, ОВ=t ,
Следовательно, с учетом вышесказанного выведите формулу для нахождения площади трапеции. Следовательно:
![]() (1)
(1)
Вспомним, чему равна скорость при равномерном
равноускоренном движении? ![]()
С учетом того, что S=Sx, формулу (1) можно переписать в ином виде. Каждый из учеников записывает получившуюся формулу в свою тетрадь. И проверяет ее с той, которую учитель выводит на доске.
Т.о. мы получили формулу для расчета проекции вектора перемещения при равноускоренном движении.
![]()
![]()
По этой же формуле рассчитывают проекцию вектора перемещения и при движении тела с уменьшающейся по модулю скоростью, только в этом случае векторы скорости будут направлены в противоположные стороны и их проекции будут иметь разные знаки.
Показ видеофрагмента «Демонстрация равноускоренного прямолинейного движения». Вопросы к учащимся по демонстрации.
Закрепление учебного материала.
Решение задач.
Рымкевич №53
За какое время автомобиль, двигаясь с ускорением 0,4 м/с2, увеличит свою скорость с 12 м/с до 20 м/с?
Задача №2.
Велосипедист съехал с горки за 5 с, двигаясь с
постоянным ускорением 0,5 ![]() .
Определить длину горки, если известно, что в начале скорость
велосипедиста была равна 18 км/ч.
.
Определить длину горки, если известно, что в начале скорость
велосипедиста была равна 18 км/ч.
-
Дано:
t=5c
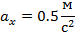
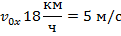
Найти
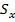
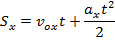
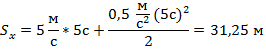
Подведение итогов урока.
Рефлексия, запись домашнего задания. Домашнее задание параграф 7,8 читать упражнение 7, вопросы после параграфа.
Урок 7.
Решение задач по теме: «Графики зависимости кинематический величин от времени при движении»
Цели урока:
Научить учащихся решать задачи на совместное движение нескольких тел. Проверить их навыки и умения решать задачи. Сформировать понятие ускорения.
Ход урока
I. Повторение. Проверка домашнего задания
-
Какое движение называют равномерным?
-
Что называется скоростью равномерного движения? В каких единицах она выражается?
-
В каких случаях проекция скорости равномерного движения на ось положительна, в каких отрицательна?
-
Как находится проекция перемещения, если известна проекция скорости?
-
Как найти координату тела в любой момент времени, если известна начальная координата, проекция скорости и время?
-
Как скорость, выраженную в метрах в секунду, выразить в километрах в час и наоборот?
-
Выразите в м/с скорость 72 км/ч.
-
Какая скорость больше: 5 м/с или 36 км/ч?
II. Решение задач
Задача 1
В течение 30 с поезд двигался равномерно со скоростью 54 км/ч. Какой путь прошел поезд за это время? (Ответ: 450 м.)
Задача 2
Движения двух велосипедистов заданы уравнениями х, = 5t и х2 = 150 - 10t.
а) Постройте графики зависимости x (t);
б) Найдите время и место встречи;
в) Постройте графики зависимости vx (t).
(Ответ: тела встретятся через t = 10 с, х = 50 м.)
Задание 3
Точка А совершает движение на плоскости XY. Координаты точки, в зависимости от времени изменяются по закону: х = -2t, у = 2 + 3t. а) Запишите уравнение траектории у (x) точки А.
2) Чему равны начальные координаты движущейся
точки и координаты
через 2 с после начала движения?
3) Постройте график функции у (х).
(Ответ: в начальный момент t - 0; х = 0. Через 2 с,x = - 4 м; у = 8 м.)
III. Самостоятельная работа
1вариант
На оси координат показаны тела их у1=40км/ч
v;=70 км
скорости (рис. 14). -• • • ►
а) Определить начальные координаты 0 60 120 х,км
первого и второго тела.
Рис 14
б) Записать для каждого тела уравнение зависимости координаты от времени х (t).
в) Найти место и время встречи аналитически и графически.
г) Построить график vx (t).
д) Найти координату каждого тела через 4 ч.
е) Найти путь, пройденный каждым телом за 6 ч.
2 вариант
На оси координат показаны тела, их
скорости.
а) Определите начальные координаты 1 и 2 тела.
б) Записать для каждого тела уравнение зависимости координаты от времени.
в) Найти место и время встречи аналитически и графически.
г) Построить график vx (t).
д) Найти координату каждого тела через 4 с.
е) Найти путь, пройденный каждым телом за 6 секунд.
IV. Новый материал
Прямолинейное равномерное движение, т.е. движение с постоянной (по модулю и направлению) скоростью, не очень часто встречается на практике.
Гораздо чаще приходится иметь дело с таким движением, при котором скорость со временем изменяется. Такое движение называется неравномерным.
Эксперимент
Рассмотрим движение шарика по наклонному желобу, а затем по горизонтальному участку (рис. 16).
Координаты шарика через 2 с представлены в таблице:
t. c О 2 4 6 8 Рис. 16
х, см I О I 8 I 32 I 72 | 128
Видно, что перемещения шарика за 2 с различны на разных этапах движения. При таком движении скорость тела (мгновенная скорость) непрерывно изменяется от точки к точке.
Для простоты будем считать, что за каждую единицу времени и вообще за любые равные промежутки времени скорость изменяется одинаково.
V. Решение задач
Для самостоятельного решения в классе учащимся можно дать следующие задачи:
Задача 1
Троллейбус, трогаясь с места, движется с постоянным ускорением 1,5 м/с2. Через какое время он приобретет скорость 54 км/ч? (Ответ: через 10 с.)
Задача 2
Автомобиль, движущийся со скоростью 36 км/ч, останавливается при торможении в течение 4 с. С каким постоянным ускорением движется автомобиль при торможении? (Ответ: 2,5 м/с2.)
Задача 3
Автомобиль, двигаясь с постоянным ускорением, на некотором участке увеличил свою скорость с 15 м/с до 25 м/с. За какое время произошло это увеличение, если ускорение автомобиля равно 1,6 м/с2? (Ответ: 6,25 с.)
Задача 4
Какая скорость могла быть достигнута, если бы тело в течение 0,5 ч двигалось с ускорением 10 м/с2 из состояния покоя? (Ответ: 18000 м/с.)
Домашнее задание
-
Выучить §5-6;
-
Упр. 5 (учебник, стр.24);
-
Задача 7 (учебник, стр. 241).
Урок 8.
Лабораторная работа №1 «Исследование равноускоренного движения без начальной скорости»
Цели урока:
-
Образовательная: определить ускорение движения шарика и его мгновенную скорость перед ударом о цилиндр. Показать применение информационных технологий в практической деятельности.
-
Развивающая: развитие логического мышления, совершенствование знаний, умений и навыков на практике.
-
Воспитательная: воспитание самостоятельности, информационной культуры.
II. Актуализация опорных знаний
I. фронтальный опрос:
- Что называется равноускоренным движением?
- Запишите формулы и назовите единицы измерения в системе СИ:
перемещения, скорости, ускорения.
Отвечают на вопросы и пишут формулы на доске.
II. Решение задачи: лыжник спускается с горы и за 20 с проходит путь 50 м. Определите ускорение лыжника и его скорость в конце спуска.Решение:
S = Vо t + аt2/2
т.к. Vо = 0
S = аt2/2
a = 2S/ t2
t = 20 c
S = 50 м
Vо = 0 м/с
Решают задачу: выводят в тетради формулу для вычисления ускорения и выполняют расчеты в электронной таблице
III. Применение знаний, умений и навыков
Сейчас вам предстоит выполнить лабораторную работу
«Исследование равноускоренного движения без начальной скорости».
Цель: определить ускорение движения шарика и его мгновенную
скорость перед ударом о цилиндр.
Для выполнения лабораторной работы вам понадобится оборудование:
штатив с муфтой и лапкой, желоб, металлический шарик, метроном,
цилиндр металлический, измерительная лента.
Собирают установку по рисунку 178 учебника Физика 9 класс, А.В. Перышкин, Е.М. Гутник.
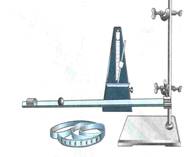
Строят таблицу.
Учитель физики: Таблица готова и вы приступаете к выполнению лабораторной работы.
Выполняют лабораторную работу по описанию в учебнике (вариант
I) и заносят измеренные и вычисленные данные в электронную
таблицу
Следит за правильностью выполнения эксперимента.
Анализируют результаты работы. Делают вывод.
Строят график по результатам эксперимента. Делают вывод о том,
что зависимость скорости тела от времени при равноускоренном
прямолинейном движении является линейной.
Учитель физики акцентирует внимание учащихся на том, что: площадь под графиком зависимости скорости движения от времени численно равна перемещению тела за время t при равноускоренном движении.
Определяют перемещение тела по графику за время, равное 1,5 с и сравнивают его с перемещением, измеренным в лабораторной работе.
IV. Итог урока
Учитель физики: Какова была цель нашего урока?
- Какие задачи были выполнены для достижения цели?
Исследовать равноускоренное движение без начальной скорости.
Повторили основные формулы равноускоренного движения и решили
задачу на определение ускорения тела при прямолинейном
равноускоренном движении без начальной скорости.
Выполнили лабораторную работу: «Исследование равноускоренного
движения без начальной скорости»
Урок 9.
Решение задач по теме: « Прямолинейное равноускоренное движение, мгновенная скорость, ускорение, перемещение»
Цели урока:
Развитие навыков самостоятельной работы. Отработка методов решения задач.
Ход урока
I. Повторение. Проверка домашнего задания
Вопросы и задачи на повторение:
- Начальная и конечная скорости движения тела (тело движется в одном направлении) соответственно равны 2 м/с и 4 м/с. Как движется это тело?
- Проекция ускорения тела равна -2 м/с2. Как это понимать?
- Поезд отходит от станции. Как направлено его ускорение?
- Поезд начинает тормозить. Как направлены его ускорение и скорость?
- Ускорение тела равно 1 м/с2. На сколько изменится скорость тела за 1 с? Далее на доске выписываются основные формулы кинематики в векторной форме и в проекциях:
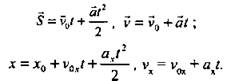
Следует анализ формул.
- Запишите, что получится, если а = 0. (х = x0 + v0xt, vx = v0x.)
Делается вывод: равномерное движение является частным случаем равноускоренного движения.
II. Самостоятельная работа
Вариант I
1. Какую скорость будет иметь тело через 20 с от начала движения, если оно движется с ускорением 0,2 м/с2? (Ответ: 4 м/с.)
2. За 5 с скорость шарика возросла с 2 м/с до 5 м/с. Определить ускорение шарика. (Ответ: 0,6 м/с2.)
3. Как движется автомобиль, график проекции скорости движения которого изображен на рис. 21?
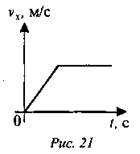
4. Автомобиль, остановившийся перед светофором, набирает затем скорость 54 км/ч на пути 50 м. С каким ускорением он должен двигаться? Сколько времени будет длиться разгон? (Ответ: 2,25 м/с2; 6,7 с.)
5. По данному на рис. 22 графику проекции ускорения построить график проекции скорости, если начальная скорость v0 = 0.
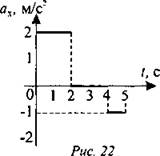
6. По наклонной доске пустили катиться снизу вверх шарик. На расстоянии 30 см от начала пути шарик побывал дважды: через 1 с и через 2 с после начала движения. Определите начальную скорость и ускорение движения шарика. Ускорение считать постоянным. (Ответ: 0,45 м/с; 0,3 м/с2.)
Вариант II
1. Через 25 с после начала движения спидометр автомобиля показал скорость движения 36 км/ч. С каким средним ускорением двигался автомобиль? (Ответ: 0,4 м/с2.)
2. Велосипедист движется под уклон с ускорением 0,2 м/с2. Какую скорость приобретет велосипедист через 10 с, если его начальная скорость равна 5 м/с? (Ответ: 7 м/с.)
3. Как движется велосипедист, график проекции скорости движения которого изображен на рис. 23?
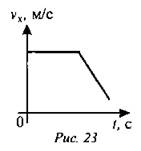
4. При равноускоренном движении из состояния покоя тело проходит за пятую секунду 90 см. Определите путь тела за седьмую секунду. (Ответ: 1,3 м.)
5. По данному на рис. 24 графику проекции ускорения построить график проекции скорости, если начальная скорость v0 = 0.
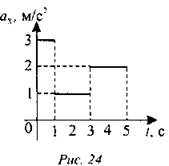
6. Первый вагон поезда прошел мимо наблюдателя, стоящего на платформе, за 1 с, а второй - за 1,5 с. Длина вагона 12 м. Найти ускорение поезда и его скорость в начале наблюдения. Движение поезда считать равноускоренным. (Ответ: 3,2 м/с2; 13,6 м/с.)
Примечание:
Из данных задач можно составить варианты работ любого уровня сложности. Например, плохо успевающим учащимся можно давать задачи 1, 2, 3. Средним - задачи 3, 4, 5. Хорошо успевающим можно предложить задачи 4, 5, 6. Возможны и другие варианты.
Домашнее задание
1. Велосипедист движется в течение некоторого времени с постоянной скоростью 2 м/с. Затем его движение становится равноускоренным, и он проходит за 20 с путь в 250 м. Какой будет конечная скорость велосипедиста? (Ответ: 23 м/с.)
2. Тело, двигаясь с ускорением 10 м/с2 из состояния покоя, в конце первой половины пути достигло скорости 20 м/с. Какой скорости достигнет тело в конце пути? Сколько времени двигалось тело? Какой путь оно прошло? (Ответ: S = 40 м, t = 2,8 с, v2 = 28 м/с.)
3. На рис. 25 представлен график зависимости проекции скорости от времени. В какой из четырех интервалов времени тело прошло максимальный путь?
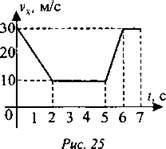
а) 0-2 с;
б) 2-5 с;
в) 5-6 с;
г) 6-7 с.
Урок 10.
Контрольная работа№1 по теме « Кинематика материальной точки»
Цели урока:
Проверить качество усвоения изученного материала. Развивать навыки устного счета.
Ход урока
Указания к работе
Содержание контрольной работы по возможности должно быть таким, чтобы в нее входили задачи, охватывающие весь изученный по теме материал. При этом расчетная часть задач должна быть несложной. Это позволит ученикам не только тратить на расчеты минимум времени, но и большую часть расчетов проводить устно. Умение логично строить ответ на поставленный вопрос - важный элемент в обучении.
Контрольная работа может быть составлена как из тестовых заданий с выбором верного ответа из нескольких предлагаемых вариантов, так и из классических качественных и расчетных задач.
Вариант №1
1.Движение тела задано уравнением x = 3 - 2t. Постройте график скорости и определите перемещение тела за 5 с.
2.Автомобиль, двигаясь с ускорением 2 м/с2 за 5 секунд прошел 125 м. Определите скорость в конце участка движения.
3.Автомобиль, скорость которого 10 м/с, начал двигаться с постоянным по модулю ускорением 0,5 м/с2, направленным в ту же сторону, что и вектор скорости. Определите скорость автомобиля через 20 с.
4.Изобразите траекторию движения иглы относительно грампластинки и относительно стола при её проигрывании.
5.В чем отличие понятий «путь» и «перемещение»? Могут ли они быть равными друг другу по величине? В каком случае?
----------------------------------------------------------------------------------------------------------------------------------
Вариант №21.На рисунке представлен график зависимости проекции скорости прямолинейно движущегося тела от времени. Найдите перемещение тела за 4 с.
2.Автомобиль двигался по прямолинейному участку шоссе с постоянной скоростью 10 м/с. Когда машина находилась на расстоянии 100 м от светофора, водитель нажал на тормоз. После этого скорость автомобиля стала уменьшаться при постоянном ускорении 3 м/с2. Найдите положение автомобиля относительно светофора через 2 с после начала торможения.
3.При торможении скорость автомобиля уменьшается от 20 до 10 м/с в течение 5 с. Найдите ускорение автомобиля при условии, что оно во время движения оставалось постоянным.
4.Что мы оплачиваем: путь или перемещение - при поездке в такси? самолете?
5.Плот равномерно плывет по реке. Сплавщик движется поперек плота с постоянной скоростью. Выберите направления движения воды и сплавщика. Изобразите траекторию движения сплавщика относительно берега и относительно плота.
-------------------------------------------------------------------------------------------------------------------------------
Вариант №3
1.По заданному уравнению скорости V = 5 + 3t запишите уравнение перемещения. Вычислите перемещение за первые 7 с движения.
2.Автомобиль, движущийся со скоростью 10 м/с, при торможении остановился через 5 с. Какой путь он прошел при торможении, если двигался равноускоренно?
3.Поезд движется со скоростью 20 м/с. При включении тормозов он стал двигаться с постоянным ускорением 0,1 м/с2. Определите скорость поезда через 30 с после начала торможения.
4.Известно, что траектории двух тел пересекаются. Столкнутся ли эти тела?
5. Начертите траекторию движения точки обода велосипедного колеса при равномерном и прямолинейном движении велосипедиста: а) относительно спиц в колесе; б) относительно рамы велосипеда; в) относительно земли.
-------------------------------------------------------------------------------------------------------------------------------
Вариант №41.Автомобиль двигался равноускоренно, и в течение 10 с его скорость увеличилась с 5 до 15 м/с. Найдите ускорение автомобиля.
2.На рисунке представлен график зависимости проекции скорости прямолинейно движущегося тела от времени. Найдите перемещение тела за 5 с.
3.Кран равномерно поднимает груз и одновременно равномерно и прямолинейно движется по рельсам. Выберите направление движения крана и изобразите траекторию движения груза относительно Земли и относительно крана.
4.Байдарка прошла 1000 м от старта до финиша со скоростью 5 м/с и после прохождения линии финиша начала тормозить с постоянным ускорением 0,5 м/с2. На каком расстоянии от линии старта окажется байдарка через 10 с после прохождения финишной черты?
5.В каком случае мгновенная и средняя скорости равны между собой? Почему?
-------------------------------------------------------------------------------------------------------------------------------
Вариант №5
1.Даны уравнения движения двух тел: x1 =2 + 0,25t и x2 = - 3 + 1,5t. Определите начальные координаты тел, скорости тел, а также место и время их встречи.
2.Тележка из состояния покоя прошла 6,25 м с ускорением 0,32 м/с2. Определите конечную скорость тележки и время её движения.
3.Автомобиль начал двигаться с постоянным ускорением 0,2 м/с2. За какое время она достигнет скорости 72 км/ч?
4.Какова траектория движения конца лопасти пропеллера самолета, движущегося равномерно и прямолинейно относительно: а) конца другой лопасти пропеллера; б) корпуса самолета; в) земли.
5.Два поезда идут навстречу друг другу: один - ускоренно на север, другой - замедленно на юг. Как направлены ускорения поездов?
-------------------------------------------------------------------------------------------------------------------------------
Вариант №61.Автомобиль через 10 с приобретает скорость 20 м/с. С каким ускорением двигался автомобиль? Через какое время его скорость станет равной 108 км/ч, если он будет двигаться с тем же ускорением?
2.По графику скорости который изображен на рисунке, определить перемещение тела за 7 с.
3.На проспекте на расстоянии 100 м от моста расположена школа. Мотоциклист, двигаясь от моста, проехал мимо школы со скоростью 5 м/с, а затем начал разгоняться с постоянным ускорением 2 м/с2. Найдите положение мотоциклиста относительно моста через 20 с после начала разгона. Траекторию движения мотоциклиста считать прямолинейной.
4.В чем разница понятий: «мгновенная скорость» и «средняя скорость»?
5.С верхней полки вагона равномерно движущегося поезда упал чемодан. Какова траектория движения чемодана относительно: а) вагона; б) земли?
-------------------------------------------------------------------------------------------------------------------------------
Вариант №7
1.Скорость движения тела задана уравнением v = 5 + 2t (единицы скорости и ускорения выражены в СИ). Чему равны начальная скорость и ускорение тела? Постройте график скорости движения тела и определите его скорость в конце пятой секунды.
2.Чему была равна начальная скорость поезда, если при торможении с ускорением 0,5 м/с2 он прошел до полной остановки путь 225 м?
3.Скорость скатывающегося с горы лыжника за 3 с увеличилась от 0,2 м/с до 2 м/с. С каким ускорением двигалось тело?
4.Можно ли считать воздушный шар материальной точкой при определении архимедовой силы Fa, действующей на шар в воздухе (Fa = rgVт)?
5.Дорожка имеет форму прямоугольника, меньшая сторона которого равна 15 м, а большая - 20 м. Человек обходит всю дорожку за 40 с. Определите перемещение и путь человека за 40 с и за 20 с.
-------------------------------------------------------------------------------------------------------------------------------
Вариант №8
1.Поезд движется со скоростью 20 м/с. Чему будет равна скорость поезда после торможения, происходящего с ускорением 0,25 м/с2, в течение 20 с?
2.Поезд движется прямолинейно со скоростью 15 м/с. Какой путь пройдет поезд за 10 с торможения, происходящего с ускорением 0,5 м/с2?
3.За какую секунду от начала равноускоренного движения тело пройдет путь, втрое больший, чем в предыдущую секунду?
4.Мяч, упав с высоты 2 м и отскочив от земли, был пойман на высоте 1 м. В обоих направлениях мяч двигался вдоль вертикальной прямой. Определите путь L и перемещение S мяча за все время движения.
5.Можно ли применять паруса и руль для управления полетом воздушного шара?
-------------------------------------------------------------------------------------------------------------------------------
Вариант №9
1.Тело, двигаясь прямолинейно со скоростью 20 м/с, начинает тормозить с ускорением 4 м/с2. Определить скорость этого тела через 4 с, 5 с, 8 с после начала торможения.2.Хоккейная шайба пересекла ледяное поле длиной 60 м за 4 с и остановилась. Какую скорость сообщил шайбе хоккеист, ударив по ней клюшкой?
3.Можно ли считать земной шар материальной точкой при определении времени восхода солнца на восточной и западной границах России?
4.Два автомобиля движутся по прямолинейному участку шоссе. На рисунке изображены графики проекций скоростей этих автомобилей на ось параллельную шоссе. Как движутся автомобили: равномерно или равноускоренно? Как направлены их скорости по отношению друг к другу?
5.На стеклах окон движущегося автобуса прямой дождь оставляет косые следы. Почему? Отчего эти следы имеют разный наклон?
-------------------------------------------------------------------------------------------------------------------------------
Вариант №10
1.За какое время автомобиль, двигаясь с ускорением 0,5 м/с2, уменьшит свою скорость с 20 м/с до 15 м/с?
2.За 5 с от начала движения автомобиль приобрел скорость 10 м/с. Какой путь он при этом прошел?3.Вы сидите в вагоне движущегося поезда и смотрите в окно на проходящий мимо встречный поезд. Когда он мимо вас промчится, вам покажется, что скорость вашего поезда уменьшилась. Почему?
4.Может ли зависимость пути от времени изображаться следующими графиками, которые представлены на рисунке?
5.Велосипедист движется равномерно по окружности радиусом 100 м и делает один оборот за 2 мин. Определите путь и перемещение велосипедиста за 1 мин и за 2 мин.
Подведение итогов.
Домашнее задание. Повторить параграф 7,8
Урок 11.
Относительность механического движения. Анализ контрольной работы.
Цели урока:
Дать учащимся представление об относительности движения.
Ход урока
I. Повторение. Проверка домашнего задания
Двое учеников выписывают на доске решения домашних задач.
II. Новый материал
Допустим, что человек, неподвижно сидящий на движущейся платформе, наблюдает за арбузом, лежащим на той же платформе. Естественно, что он мысленно свяжет систему отсчета с платформой. Для него (или в системе отсчета, связанной с платформой) арбуз находится в покое.
В это же время человек, находящийся у полотна железной дороги, мысленно связав систему отсчета с землей, увидит, что арбуз движется.
Рассмотренный пример показывает, что одно и тоже тело движется в разных системах отсчета по-разному: в системе отсчета, связанной с платформой, арбуз находится в покое, а относительно системы отсчета, связанной с землей, движется. Поэтому движение относительно.
Ребенок, впервые попавший на берег реки во время ледохода, спросил: «На чем это мы едем?» (Ребенок «выбрал» в качестве тела отсчета плывущую по реке льдину.) Находясь в покое относительно берега, ребенок двигался вместе с берегом относительно «выбранной» им системы отсчета - льдина.
В стихотворении И. А. Бунина «В поезде» есть такие строки:
Вот мост железный над рекой
Промчался с грохотом под нами ...
- Что писатель-пассажир выбрал за систему отсчета? (Писатель «выбрал» систему отсчета, связанную с поездом. Поэтому поезд условно считается неподвижным. Относительно этой системы отсчета мост в самом деле движется.)
Обратите внимание, в двустишии отмечается также, что не только движение тела, но и его положение относительно: мост расположен под поездом, но над рекой.
Еще один пример относительности движения и покоя. Всем, наверное, известно, как трудно, находясь в вагоне поезда и глядя в окно на проходящий мимо по соседнему пути поезд, выяснить, какой из поездов движется, а какой покоится. Строго говоря, если видеть только соседний вагон и не видеть землю, строения и т. д., то узнать, какой из поездов движется прямолинейно равномерно, а какой - покоится, невозможно. Утверждение пассажиров, что его поезд движется, а другой стоит, будет справедливо для обоих поездов, т. к. движение и покой относительны.
Пример 1
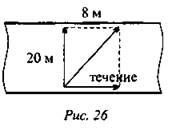
Пловец пересек реку шириной 20 м, выдерживая курс поперек реки
(рис. 26). В то же время течение реки его снесло на расстояние 8 м.
Каков модуль суммарного перемещения пловца? (Ответ: модуль
суммарного перемещения ![]() .)
.)
Пример 2
Пассажир, находящийся в вагоне поезда, проходит по направлению его движения 20 м. Каков модуль перемещения пассажира относительно Земли, если за то же время поезд прошел 200 м? Все движения прямолинейные. А если пассажир идет против поезда? (Ответы: 220 м и 180 м.)
Пример 3
В условиях примера 2 определите, каков модуль перемещения пассажира, поезда и земли в системе отсчета, связанной с пассажиром? (S = 0, S11 = 20 м, S3 = 220 м или S3 = 180 м).
Понятия того, что движение одного и того же тела можно рассматривать в разных системах отсчета, сыграло огромную роль в развитии взглядов на строение Вселенной.
Идея о вращении планет вокруг Солнца (гелиоцентризм) возникла еще в Древней Греции (Гераклий Понтийский, Аристарх Самосский...), но в дальнейшем почти на двадцать веков была забыта отчасти из-за противоречивости ощущений и утверждения о движении Земли, отчасти из-за преследований со стороны церкви. Николай Коперник, живший в XVI в., получил отличное образование в университетах Польши и Италии (математика, астрономия, право, языки, медицина). Почти всю свою жизнь он провел в должности каноника Всермийской епархии, занимался устройством самых разнообразных дел, свободное время отдавал астрономии. Титаническая работа, которая сопровождалась наблюдениями и вычислениями продолжалась в течение почти двадцати лет. Книга Коперника «О вращении небесных сфер» вышла в 1543 г. В этом труде земной шар низводился в ранг рядовой планеты, движущейся, как и остальные, по орбите вокруг Солнца и вращающейся вокруг оси. Книгу внесли в «Индекс запрещенных».
III. Решение задач
Задача 1
Эскалатор метро движется со скоростью 0,75 м/с. Найти время, за которое пассажир переместился на 20 м относительно земли, если он сам идет в направлении движения эскалатора со скоростью 0,25 м/с в системе отсчета, связанной с эскалатором. (Ответ: 20 с.)
Задача 2
Два поезда движутся навстречу друг другу со скоростями 72 км/ч и 54 км/ч. Пассажир, находящийся в первом поезде, замечает, что второй поезд проходит мимо него в течение 14 с. Какова длина второго поезда?
Дано:
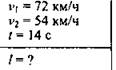
Решение:
72 км/ч = 20 м/с; 54 км/ч = 15 м/с.
Суммарная скорость движения поездов относительно друг друга:
![]()
Ответ: l = 490 м.
Задача 3
Эскалатор метро поднимает неподвижно стоящего на нем пассажира в течение 1 минуты. По неподвижному эскалатору пассажир поднимается за 3 минуты. Сколько времени будет подниматься идущий вверх пассажир по движущемуся эскалатору. (Ответ: 45 с.)
Задача 4
Самолет движется относительно воздуха со скоростью 50 м/с. Скорость ветра относительно земли 15 м/с. Какова скорость самолета относительно земли, если он движется по ветру? Против ветра? Перпендикулярно направлению ветра? (Ответ: v1 = 65 м/с, v2 = 35 м/с, v3 = 52 м/с.)
Домашнее задание
1. Выучить § 9, ответить на вопросы к параграфу;
2. Упражнение 9;
3. Решить задачу (для желающих):
Скорость катера перпендикулярна скорости реки vp и относительно берега равна vк1 = 4 м/с. Чему равна скорость реки, если скорость катера относительно воды равна vк2 = 5 м/с? (Ответ: vp = 3 м/с.)
Урок 12.
Инерциальные системы отсчета. I закон Ньютона
Цели урока:
Сформировать понятие об инерциальной системе отсчета. Изучить I закон Ньютона. Показать важность такого раздела физики как «Динамика».
Ход урока
I. Повторение
- В чем состоит основная задача механики?
- Зачем введено понятие материальной точки?
- Когда тело можно считать материальной точкой? Приведите примеры.
- Что такое система отсчета? Для чего она вводится?
- Какие виды систем координат вы знаете
II. Новый материал
В главном разделе механики - динамике - рассматривается взаимное действие тел друг на друга, которое является причиной изменения движения тел, т.е. их скоростей.
Если кинематика отвечает на вопрос: как движется тело?, то динамика выясняет, почему именно так.
В основе динамики лежат три закона Ньютона.
Если неподвижно лежащее на земле тело начинает двигаться, то всегда можно обнаружить предмет, который толкает это тело, тянет или действует на него на расстоянии (например, если к железному шарику поднесем магнит).
Эксперимент 1
Возьмем кусок мела в руки и разожмем пальцы: мел упадет на пол.
- Какое тело подействовало на мел? (Земля.)
Эти примеры говорят о том, что изменение скорости тела всегда вызывается воздействием на данное тело каких-либо других тел. Если на тело не действуют другие тела, то скорость тела никогда не меняется, т.е. тело будет покоиться или двигаться с постоянной скоростью.
Этот факт совсем не является само собой разумеющимся. Понадобился гений Галилея и Ньютона, чтобы его осознать.
Начиная с великого древнегреческого философа Аристотеля, на протяжении почти двадцати веков, все были убеждены: для поддержания постоянной скорости тела необходимо, чтобы что-то (или кто-то) действовало на него. Аристотель считал покой относительно Земли естественным состоянием тела, не требующим особой причины.
В действительности же свободное тело, т.е. тело, которое не взаимодействует с другими телами, может сохранять свою скорость постоянной сколь угодно долго или находиться в покое. Только действие со стороны других тел способно изменить его скорость. Если бы не было трения, то автомобиль при выключенном двигателе сохранял бы свою скорость постоянной.
Первый закон механики, или закон инерции, как его часто называют, был установлен еще Галилеем. Но строгую формулировку этого закона дал и включил его в число основных законов физики Ньютон. Закон инерции относится к самому простому случаю движения - движению тела, на которое не оказывают другие тела. Такие тела называют свободными телами.
Первый закон Ньютона формулируется так:
Существуют такие системы отсчета, относительно которых тела сохраняют свою скорость неизменной, если на них не действуют другие тела.
Такие системы отсчета называют инерциальными.
Систему отсчета, связанную с Землей можно приближенно считать инерциальной, но гораздо точнее брать за инерциальную систему отсчета, связанную с Солнцем. Строго говоря, Солнце и Земля не являются инерциальными системами отсчета. Но эффекты, вызванные этой неинерциальностью, незначительны. В ряде случаев ими пренебрегают (но далеко не всегда).
Кроме того, нельзя поставить ни одного опыта, который бы в чистом виде показал, как движется тело, если на него не действуют другие тела. Но имеется один выход: надо поставить тело в условия, при которых влияние внешних воздействий можно делать все меньше и меньше, и наблюдать, к чему это ведет.
Явление сохранения скорости тела при отсутствии действия на него других тел называется инерцией.
Эксперимент 2
Подвесим шарик на шнуре. Пока шнур не перерезан, шарик находится в покое. Если бы можно было убрать Землю, но при этом сохранить действие натянутого шнура, то он бы стал двигаться с ускорением в противоположную сторону.
- О чем говорит этот пример?
III. Закрепление изученного
Вопросы для закрепления:
- В чем состоит явление инерции?
- В чем состоит 1 закон Ньютона?
- При каких условиях тело может двигаться прямолинейно и равномерно?
- Какие системы отсчета используются в механике?
- Гребцы, пытающиеся заставить лодку двигаться против течения, не могут с этим справиться, и лодка остается в покое относительно берега. Действие каких тел при этом компенсируется?
- Яблоко, лежащее на столике равномерно движущегося поезда, скатывается при резком торможении поезда. Укажите системы отсчета, в которых первый закон Ньютона: а) выполняется; б) нарушается. (В системе отсчета, связанной с Землей, первый закон Ньютона выполняется. В системе отсчета, связанной с вагоном, первый закон Ньютона не выполняется.)
- Каким опытом внутри закрытой каюты корабля можно установить, движется ли корабль равномерно и прямолинейно или стоит неподвижно? (Никаким.)
Задачи и упражнения на закрепление:
С целью закрепления материала можно предложить ряд качественных задач по изученной теме, например:
1. Может ли шайба, брошенная хоккеистом, двигаться равномерно по льду?
2. Назовите тела, действие которых компенсируется в следующих случаях: а) айсберг плывет в океане; б) камень лежит на дне ручья; в) подводная лодка равномерно и прямолинейно дрейфует в толще воды; г) аэростат удерживается у земли канатами.
3. При каком условии пароход, плывущий против течения, будет иметь постоянную скорость?
Можно предложить и ряд чуть более сложных задач на понятие инерциальной системы отсчета:
1. Система отсчета жестко связана с лифтом. В каких из приведенных ниже случаях систему отсчета можно считать инерциальной? Лифт: а) свободно падает; б) движется равномерно вверх; в) движется ускоренно вверх; г) движется замедленно вверх; д) движется равномерно вниз.
2. Может ли тело в одно и то же время в одной системе отсчета сохранять свою скорость, а в другой - изменять? Приведите примеры, подтверждающие ваш ответ.
3. Строго говоря, связанная с Землей система отсчета не является инерциальной. Обусловлено ли это: а) тяготением Земли; б) вращением Земли вокруг своей оси; в) движением Земли вокруг Солнца?
Домашнее задание
1. § 10 читать
Урок 13.
II закон Ньютона.
Цели урока:
Ввести понятия силы как количественной меры. Изучить второй закон Ньютона.
Ход урока
I. Повторение. Проверка домашнего задания
- Как движется тело, если на него не действуют другие тела?
- Тело движется прямолинейно и равномерно. Меняется ли при этом его скорость? Чему равно ускорение тела?
- Какие взгляды относительно состояния покоя и движения тел существовали до начала XVII в.?
- Чем точка зрения Галилея, касающаяся движения тел, отличается от точки зрения Аристотеля?
- Как формулируется первый закон Ньютона?
- Какие системы отсчета называются инерциальными, а какие - неинерциальными?
- Можно ли в ряде случаев считать инерциальными системы отсчета, связанные с телами, которые покоятся или движутся прямолинейно и равномерно относительно Земли?
- Инерциальна ли система отсчета, движущаяся с ускорением относительно какой-либо инерциальной системы?
II. Сила. Второй закон Ньютона
Эксперимент
Тележка с прикрепленной к ней упругой пластинкой. Пластинка согнута и связана нитью. Тележка находится в покое относительно стола.
- Начнет ли тележка двигаться, если пластинка выпрямится? Тележка остается на месте.
Теперь поставим на другую сторону от согнутой пластинки еще одну такую же тележку (см. рис. 31). После пережигания нити обе тележки пришли в движение. Оба тела действуют друг на друга - они взаимодействуют.
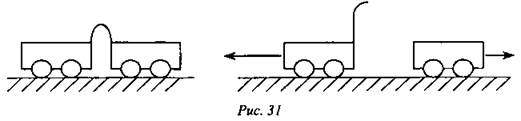
Количественную меру действия тел друг на друга, в результате которого тела получают ускорения (т.е. изменяют свою скорость), называют силой.
Общепринятое обозначение силы - ![]() (от force - сила).
(от force - сила).
Сила, как векторная величина, определяется:
♦ модулем;
♦ направлением;
♦ точкой приложения.
В реальных условиях редко встречаются случаи, когда на тело действует только одна сила. Обычно их несколько. Сила, равная геометрической сумме всех приложенных к телу (материальной точке) сил, называется равнодействующей или результирующей:
![]()
где n - число сил.
Когда на тело действует сразу несколько сил, то оно движется с
ускорением в том направлении, куда направлена равнодействующая всех
сил![]() .
.
В инерциальной системе отсчета ускорение тела прямо пропорционально равнодействующей сил, приложенных к телу и обратно пропорционально его массе (II закон Ньютона).
![]()
где ![]() -
равнодействующая всех сил, приложенных к телу [Н];
-
равнодействующая всех сил, приложенных к телу [Н];
m - масса [кг];
![]() -
ускорение [м/с2].
-
ускорение [м/с2].
Особенности II закона Ньютона:
♦ закон справедлив для любых сил;
♦ сила F является причиной и определяет ускорение ![]() ;
;
♦ вектор ускорения сонаправлен с вектором силы;
♦ если на тело действуют несколько сил, то берется результирующая;
♦ Если результирующая сила равна нулю, то ![]() = 0, т. е. получаем
первый закон Ньютона.
= 0, т. е. получаем
первый закон Ньютона.
IV. Упражнения и вопросы для повторения
Даны графики зависимости проекции скорости и ускорения от времени для прямолинейного движения тела (рис. 33). Укажите, на каких участках действия окружающих тел скомпенсированы. Как направлена равнодействующая сила по отношению к направлению движения?
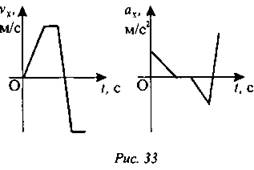
Домашнее задание
1. Выучить § 11 правила учить наизусть.
2. Выполнить упражнения 11 (1,2), 12 (3).
Урок 14.
III закон Ньютона
Цели урока:
Ввести понятия силы как количественной меры. Изучить третий закон Ньютона.
Ход урока
I. Повторение. Проверка домашнего задания
-
Как движется тело, если на него не действуют другие тела?
-
Тело движется прямолинейно и равномерно. Меняется ли при этом его скорость? Чему равно ускорение тела?
-
Какие взгляды относительно состояния покоя и движения тел существовали до начала XVII в.?
-
Чем точка зрения Галилея, касающаяся движения тел, отличается от точки зрения Аристотеля?
-
Как формулируется первый закон Ньютона
-
Инерциальна ли система отсчета, движущаяся с ускорением относительно какой-либо инерциальной системы?
II. Третий закон Ньютона
Если вы ударите ногой по футбольному мячу, то немедленно ощутите обратное действие на ногу. Нельзя толкнуть плечом кого-либо, не испытав обратного действия на наше плечо. Приложите на гладкий стол два сильных магнита разноименными полюсами, и вы увидите, что они начнут двигаться навстречу друг другу.
Если магниты поставить на тележки, закрепив их одинаковыми мягкими пружинами, то пружины растянутся совершенно одинаково. Это означает, что на оба тела со стороны пружины действуют одинаковые по модулю и противоположные по направлению силы:
![]()
На основе этого и подобных опытов можно сформировать третий закон Ньютона.
Силы, с которыми тела действуют друг на друга, равны по модулю и направлены вдоль одной прямой в противоположные стороны.
Особенности III закона Ньютона:
♦ силы появляются только парами;
♦ всегда применяется при взаимодействии тел;
♦ обе силы - одной природы;
♦ силы не уравновешиваются, т. к. приложены к разным телам;
♦ закон верен для любых сил.
IV. Упражнения и вопросы для повторения
Даны графики зависимости проекции скорости и ускорения от времени для прямолинейного движения тела (рис. 33). Укажите, на каких участках действия окружающих тел скомпенсированы. Как направлена равнодействующая сила по отношению к направлению движения?

Домашнее задание
1. Выучить §12;
Урок 15.
Решение задач по теме: «Законы Ньютона»
Цели урока:
В интересной игровой форме обобщить, закрепить знания, полученные по теме, научить видеть проявления изученных закономерностей в окружающей жизни, совершенствовать навыки решения качественных и расчетных задач, расширить кругозор учащихся, развить коммуникативные способности.
Эпиграфы к уроку:
Сделал, что мог, пусть другие сделают лучше.
Не знаю, чем я могу казаться миру, но самому себе я кажусь мальчиком, играющим у моря, которому удалось найти более красивый камешек, чем другим: но океан неизвестного лежит передо мной.
Исаак Ньютон (1643-1727 гг.)
Оформление:
Плакат с эпиграфом, портрет Ньютона, выставка литературы для дополнительного чтения.
Подготовка к уроку:
Ребята делятся на две команды, равные по силам, выбираются капитаны команд. Перед уроком каждая команда изучает литературу по истории жизни и деятельности Ньютона, приносит книги на урок.
Ход урока
Вступительное слово учителя
Учитель зачитывает и поясняет слова эпиграфа, отмечает, что, по мнению Ньютона, законы были открыты «играючи». Просто необходимо было более внимательно отнестись к окружающему миру, полному неизведанного. Поэтому и урок, посвященный законам Ньютона, проводится в виде игры, которая позволит проявиться всем способностям учащихся, расширит их кругозор, научит видеть изученные на уроках закономерности в природе, поможет объяснить многие механические явления.
I. Конкурс «Доверяй, но проверяй»
Капитаны выбирают по два лучших экспериментатора в каждой команде, которые получают экспериментальные задания и приступают к их выполнению. Через несколько минут они представят классу сам опыт и анализ его результатов. Лучший доклад приносит победу команде, а докладчику - балл в личную «копилку».
Задание для первой команды
Положите на стакан открытку. Поставьте на открытку прищепку, чтобы она находилась над серединой стакана. Резко и с силой щелкнете по открытке пальцем, чтобы она отлетела в сторону. Повторите это несколько раз.
Иногда прищепка падает в стакан в своем прежнем положении, а иногда, падая, переворачивается. Почему?
(Щелкая пальцем по открытке, вы прилагаете к ней силу. Открытка сдвигается с места так быстро, что не успевает увлечь прищепку за собой. Прищепка падает вниз благодаря силе тяжести, потому что открытка больше не поддерживает ее. Если Вы толкнете открытку с недостаточной силой, она потащит прищепку за собой, а ста тяготения потянет верхушку прищепки вниз, в результате чего она перевернется.)
Задание для второй команды «Шарик, танцующий в воздухе»
Примерно за 100 лет до нашей эры александрийский ученый Герон проделал такой опыт: на конец изогнутой трубки он поместил легкий шарик и затем начал нагнетать в трубку воздух. Шарик, поднявшись над концом трубки, как бы плясал в воздушной струе, не отлетая в сторону.
Такой опыт можно повторить, если Вы поместите мячик от пинг-понга в струю воздуха, выходящего из работающего пылесоса.
Этот же опыт можно показать и с водой. Соедините один конец резиновой трубки с водопроводным краном, другой наденьте на стеклянную трубку концом вверх. Над трубкой укрепите небольшое кольцо, в которое поместите деревянный шарик. Постепенно открывайте кран водопровода. Струя поднимает шарик.
(Если вода обтекает шарик равномерно, он будет держаться на определенной высоте. Если же шарик выйдет из равновесия, то произойдет следующее: одна часть шарика потеряет точку опоры, на другую же вода продолжает давить с прежней силой. Таким образом, шарику сообщается вращательное движение.)
II. Конкурс «Колесо истории»
В этом конкурсе участвует весь класс. Учитель задает вопросы, касающиеся истории жизни и деятельности Ньютона. Верный ответ приносит балл в «копилку» команды и в личную «копилку» отвечавшего.
Вопросы конкурса «Колесо истории»
1. Назовите дату рождения Исаака Ньютона. (25 декабря 1642 г. по старому стилю, 4 января 1643 г. по новому стилю.)
2. В каком университете (и колледже) учился Ньютон с 1661 г.? (Кембриджский университет, колледж святой Троицы (Тринити-колледж).)
3. Студенты колледжа по происхождению и имущественному положению делились на группы. Высшую группу составляли «коммонеры», платившие наиболее высокую плату и получавшие право обедать вместе с членами колледжа. Основную массу студентов составляли «пенсионеры», платившие полную плату, но не имевшие особых привилегий; за ними следовали «сайзеры», платившие меньше «пенсионеров» и, обязанные за это прислуживать членам колледжа, и, наконец, «субсайзеры», освобожденные от платы, но зато, обязанные обслуживать бакалавров, магистров и более обеспеченных студентов.
К какой группе принадлежал Ньютон? (Ньютон был принят в Тринити-колледж субсайзером, и его самолюбие очень страдало от унизительного положения слуги, в которое он был поставлен вследствие скромного имущественного положения своей семьи.)
4. Сколько лет было Ньютону, когда он стал профессором Кембриджского университета? (27 лет. С тех пор Кембридж стал славиться не богословием, а физикой и математикой, получение же кафедры, на которой работал Ньютон, стало делом чести для английских ученых.)
5. В какой области физики работал Ньютон в первые годы профессорской деятельности? (Оптика. Он усовершенствовал модель нового типа темсиона-рефлектора, открыл явление дисперсии.)
6. В 1696 г. министр финансов Англии Монтегю вспомнил о своем великом друге Ньютоне и решил привлечь его к делу оздоровления финансов стран. Какое предложение получил от него Ньютон? (15 марта 1696 г. он получил официальное извещение от Монтегю о назначении его, Ньютона, хранителем Монетного двора. Кембриджский период жизни Ньютона закончился, начался последний, лондонский период - период общественного признания заслуг Ньютона и его прижизненной славы.)
7. В какой работе Ньютона изложены его знаменитые законы? (1687 г. «Математические начала натуральной философии». Эта книга оказала огромное влияние па развитие науки и научного мышления. В ней Ньютон дает образец научного подхода к явлениям природы и техники, вооружает науку точным методом, определяет развитие физики на целых два столетия вперед.)
8. От единичного факта - падения яблока - Ньютон приходит к грандиозному обобщению. Какому? (В 1667 г. Ньютон формулирует закон всемирного тяготения, лежащий в основе небесной механики.)
9. Достиг ли Ньютон вершин славы и признания при жизни? (В 1705 г. королева Анна возвела его в рыцарское достоинство. В Королевском обществе он пользовался непререкаемым авторитетом, был богат и окружен вниманием своей племянницы.)
10. Где похоронен Ньютон? (Ньютон скончался в ночь с 20 на 21 марта 1727 г. Его похоронили с большими почестями в Вестминстерском аббатстве, английском национальном пантеоне. Надпись на памятнике над его могилой заканчивается словами: «Пусть смертные радуются, что существовало такое украшение человеческого рода». На статуе Ньютона в Кембридже высечен стих из Лукреция: «Разумом он превосходит род человеческий.)
III. Конкурс «Головоломки»
В этом конкурсе участвуют по два лучших игрока от каждой команды, которые получают задание и приступают к их выполнению. Через несколько минут они должны будут предоставить решение головоломок. Лучший приносит победу команде, а докладчик получает балл в личную «копилку».
Головоломка для первой команды
См. рисунок 34.
Подсказка: Прочитайте изречение И. Ньютона, двигаясь по часовой стрелке, пропуская определенное количество кружков.
(Ответ: «Гипотез не сочиняю».)
Головоломка для второй команды
См. рисунок 35.
Подсказка: Вырежьте затемненные клеточки в первом квадрате, наложите его на второй. Поворачивая его четыре раза, прочитаете слова Рене Декарта.
(Ответ: «Дайте мне материю и движение, и я построю мир».)
IV. Игра «Интересные вопросы»
Команды задают друг другу интересные вопросы, подготовленные заранее. Дается время на обсуждение (1-2 минуты). За правильный ответ команде дается 1 балл, баллы в личном зачете присуждает капитан команды.
Возможные вопросы
1. Если действие, как гласит закон, всегда равно и противоположно противодействию, то сила, с которой лошадь тянет телегу вперед, равна по модулю и противоположна по направлению силе, с которой телега «тянет» лошадь назад. Но телега движется вперед, а лошадь назад не движется. Почему и телега, и лошадь движутся вперед?
(Сила, действующая на телегу, и сила, действующая на лошадь, в каждый момент времени равны; но так как телега свободно перемещается на колесах, а лошадь упирается в землю, то понятно, почему телега катится в сторону лошади.)
2. Яблоко падает на землю оттого, что его притягивает земной шар; но точно с такой же силой и яблоко притягивает к себе всю нашу планету. Отчего мы говорим, что яблоко падает на землю, вместо того чтобы сказать: «Яблоко и земля падают друг на друга»?
(Яблоко и земля действительно падают друг на друга, но скорость этого падения различна для яблока и для земли. Равные силы взаимного притяжения сообщают яблоку ускорение 10 м/с2, а земному шару - во столько же раз меньше, во сколько раз масса земли превышает массу яблока. Конечно, масса земного шара в неимоверное число раз больше массы яблока, и поэтому Земля получает перемещение настолько ничтожное, что практически его можно считать равным нулю.)
3. История о том, как «Лебедь, Рак да Щука везти с поклажей воз взялись», известна всем. Но если рассматривать эту басню с точки зрения механики, результат получается вовсе не похожий на вывод баснописца Крылова. Каким он будет?
... Лебедь рвется в облака,
Рак пятится назад,
А щука тянет в воду.
(Басня утверждает, что «воз и ныне там», другими словами, что равнодействующая всех приложенных к возу сил равна нулю. Лебедь, рвущийся в облака, не мешает работе рака и щуки, даже помогает им: тяга лебедя, направленная против силы тяжести, уменьшает трение колес о землю и об оси, облегчая тем вес воза. Они направлены под углом друг к другу, следовательно, их равнодействующая не может равняться нулю.)
V. Блицтурнир
Каждой команде задается по пять вопросов, на обсуждение каждого вопроса дается 10 с. Кто быстрее и правильнее отвечает на вопрос, тот и победил. За победу присуждается балл. Участник правильно и быстро ответивший на вопрос получает балл в свою личную «копилку».
Вопросы для первой команды
- Как движется тело, если на него не действуют другие тела?
- Тело движется прямолинейно и равномерно. Меняется ли при этом его скорость?
- Как читается первый закон Ньютона (в современной формулировке)?
- Инерциальна ли система отсчета, движущаяся с ускорением относительно какой-либо инерциальной системы?
- Что является причиной ускоренного движения тел?
Вопросы для второй команды
- Как читается второй закон Ньютона?
- Как читается третий закон Ньютона?
- Какие системы отсчета называются инерциальными?
- Какие системы отсчета называются неинерциальными?
- Выразите единицу силы через единицы массы и ускорения.
VI. Подведение итогов. Награждение победителей
VII. Заключительное слово учителя
Биографы Ньютона рассказывают, что первое время в школе он учился очень посредственно. И вот однажды его обидел лучший ученик в классе. Ньютон решил, что самая страшная месть для обидчика - отнять у него место первого ученика. Дремавшие в Ньютоне способности проснулись, и он с легкостью затмил своего соперника.
Разбуженного джина познания нельзя снова спрятать в темную заплесневелую бутылку. С того счастливого для мировой науки эпизода начался процесс превращения скромного английского школьника в великого ученого.
Урок 16.
Движение тела брошенного вертикально вверх.
Цели урока:
Дать понять, что движение падающего тела является равноускоренным движением. Получить основные формулы для такого движения.
Ход урока
I. Новый материал
Одним из наиболее распространенных видов движения с постоянным ускорением - свободное падение тел.
При падении тела на Землю из состояния покоя его скорость увеличивается. Земля сообщает телам ускорение, которое направлено вниз вертикально.
Долгое время считалось, что Земля сообщает разным телам различное ускорение. И опыт вроде бы говорит о том же. (Сравните падение листа бумаги, скомканного листа бумаги, птичьего пера и камня.) Камень падает быстрее. Так считал Аристотель: чем тяжелее тело, тем быстрее оно падает.
И только Галилею впервые удалось опытным путем доказать, что это
не так. Важно учитывать сопротивление воздуха, именно оно искажает
картину. Галилей установил, что свободное падение является
равноускоренным движением. Он догадался, что можно как бы
«замедлить» свободное падение, изучая движение шаров по наклонному
желобу. При этом он получил формулу ![]()
Галилей обнаружил, что шары одинакового диаметра, но
изготовленные из разного материала движутся по желобу с одинаковым
ускорением ![]()
Данный факт учитель может продемонстрировать на опыте.
Итак, ускорение свободно падающих тел не зависит от их массы. Для проверки этой гипотезы Галилей по преданию наблюдал падение со знаменитой Пизанской башни различных тел: пушечного ядра и мушкетной пули. Все тела достигали поверхности практически одновременно.
Впоследствии были созданы вакуумные насосы, которые позволили осуществить в откачанных трубках действительно свободное падение тел.
Эксперимент 1
Трубка Ньютона: В стеклянной трубке помещается дробинка, кусочек пробки, пушинка и т. д. Если перевернуть трубку, то быстрее всего упадет дробинка, медленнее - пушинка. Если же выкачать из трубки воздух, то пушинка будет падать, не отставая от дробинки.
- Почему во втором случае все тела падают одновременно? (Движение пушинки задерживалось сопротивлением воздуха, которое в меньшей степени сказывалось на движении дробинки.)
На поверхности Земли ускорение свободного падения (g) меняется в пределах от 9,78 м/с2 на экваторе до 9,83 м/с2 на полюсе. При решении многих задач можно принимать g вблизи поверхности Земли равным 9,8 м/с2или даже более грубо 10 м/с2.
При падении тел в воздухе на их движение влияет сопротивление воздуха. Поэтому ускорение тел в этом случае уже не равно g. При больших скоростях сопротивление воздуха существенно и его влиянием нельзя пренебречь.
Движение тела по вертикали вниз
Запишем уравнения для скорости и перемещения при равноускоренном
движении с учетом, что ![]()
![]()
При v0 = 0 скорость тела в свободном падении в произвольный момент времени t равна v = gt.
Путь при v0 = 0 равен ![]()
В этом случае скорость тела в свободном падении после
прохождения путиh равна ![]() а продолжительность падения
а продолжительность падения
![]()
Движение тела, брошенного вертикально вверх
Т. к. в верхней точке скорость v = 0, то начальная скорость
брошенного тела v0 = gt. Следовательно, время подъема:
![]() A
скорость тела в момент времени t: v = v0 - gt.
A
скорость тела в момент времени t: v = v0 - gt.
Максимальная высота подъема тела ![]()
II. Упражнения и вопросы для повторения
- Что называется свободным падением тел? При каких условиях падение тел можно считать свободным?
- Каким видом движения является свободное падение тел?
- Зависит ли ускорение свободного падения тел от массы?
- Как изменится ускорение падающего тела, если толкнем тело вниз, сообщив ему начальную скорость?
- Напишите формулы, описывающие свободное падение тел.
- С каким ускорением движется тело, брошенное вверх? Чему равно и как направлено это ускорение?
- Чем объясняется то, что все тела, независимо от их массы, движутся как при падении, так и при движении тела, брошенного вертикально вверх, с одинаковым ускорением?
- Учитывается ли сопротивление воздуха в полученных выше формулах, описывающих свободное падение и движение тела, брошенного вертикально вверх?
- Напишите формулы, описывающие движение тела, брошенного вертикально вверх.
Вопросы могут быть использованы на следующем уроке в качестве повторения.
III. Решение задач
Задача 1
Тело падает с высоты 57,5 м (v0 = 0). Сколько времени падает тело и какова его скорость при ударе о землю? (Ответ: t = 3,4 с, v = 34 м/с.)
Задача 2
Стрела выпущена из лука вертикально вверх с начальной скоростью v0 = 30 м/с. На какую максимальную высоту поднимется стрела? (Ответ: h = 45 м.)
Задача 3
Тело свободно падает с высоты 20 м над землей. Какова скорость тела в момент удара о землю? На какой высоте его скорость вдвое меньше? (Ответ:v = 20 м/с, h = 15 м.)
Домашнее задание
1. Выучить § 14; читать
2. Выполнить упражнения 13, 14;
3. Ответить на вопрос микротеста:
Мяч брошен вертикально вверх со скоростью 20 м/с. На какое расстояние от поверхности земли он удалится за 2 с?
а) на 60 м;
б) на 40 м;
в) на 20 м;
г) на 10 м.
Урок 17.
Закон всемирного тяготения. Невесомость.
Цели урока:
обучающая: формирование понятия «гравитационные
силы»; изучение закона всемирного тяготения, границ его
применимости, знакомство с опытным определением гравитационной
постоянной; раскрытие понятия «взаимодействие тел» на примере
закона всемирного тяготения и ознакомление с областью
гравитационных сил;
развивающая: развитие умений анализировать учебный материал:
наблюдать, сравнивать, сопоставлять изучаемые явления, факты,
делать выводы; развитие умственной деятельности, целостности
восприятия и умений анализировать знания;
воспитательная: воспитание познавательного интереса культуры
умственного труда и естественно-материалистического
мировоззрения.
Ход урока
I. Организационный момент. Объявление темы целей урока.
II. Актуализация опорных знаний .
Проверка домашнего задания
Начнем с того, что мы уже знаем. Вспомним и ответим на следующие вопросы:
1. Что называется свободным падением тела?
2. Что такое ускорение свободного падения?
3. Почему в воздухе кусочек ваты падает с меньшим ускорением, чем
железный шарик?
4. Кто первым пришел к выводу о том, что свободное падение является
равноускоренным движением?
5. Действует ли сила тяжести на подброшенное вверх тело во время
его подъема.
6. С каким ускорением движется подброшенное вверх тело при
отсутствии сопротивления воздуха?
Вариант I.
1.В трубке, из которой откачан воздух, на одной и той же высоте находятся дробинка, пробка и птичье перо. Какое из тел быстрее достигнет дна трубки?
А) дробинка,
Б) пробка,
В) птичье перо,
Г) все тела достигнут дна одновременно.
2.Чему равна скорость свободно падающего тела через 4 сек.
А) 20 м/с,
Б) 80 м/с,
В) 40 м/с,
Г) 160 м/с.
3. Какой путь пройдет свободно падающее тело за 3 сек?
А) 15 м,
Б) 45 м,
В) 30 м,
Г) 90 м.
4. Какой путь пройдет свободно падающее тело за 5-ю сек?
А) 45 м,
Б) 50 м,
В) 125 м,
Г) 250 м.
Вариант II.
1.В трубке, с воздухом, при атмосферном давлении, на одной и той же высоте находятся дробинка, пробка и птичье перо. Какое из тел быстрее достигнет дна трубки?
А) дробинка,
Б) пробка,
В) птичье перо,
Г) все тела достигнут дна одновременно.
2.Чему равна скорость свободно падающего тела через 3 сек.
А) 15 м/с,
Б) 45 м/с,
В) 30 м/с,
Г) 90 м/с.
3. Какой путь пройдет свободно падающее тело за 4 сек?
А) 20 м,
Б) 160 м,
В) 40 м,
Г) 80 м.
4. Какой путь пройдет свободно падающее тело за 7-ю сек?
А) 65 м,
Б) 245 м,
В) 70 м,
Г) 490 м.
III. Основная часть. Изучение нового материала
Из истории физики .Сопровождение учебной презентацией
+видеоролики.Слайды 1-6
Заполнение опорного конспекта.
Датский астроном Тихо Браге (1546-1601), долгие годы наблюдавший за
движением планет, накопил огромное количество интересных данных, но
не сумел их обработать, перед смертью передал их своему ученику
Иоганну Кеплеру. Поиски точных законов гелиоцентрического мира
стали делом всей его жизни. Он открыл три закона движения планет,
но Кеплер не сумел объяснить динамику движения. Почему планеты
обращаются вокруг солнца именно по таким законам?
Иоганн Кеплер (1571-1630), используя идею Коперника о
гелиоцентрической системе и результаты наблюдений Тихо Браге
установил законы движения планет вокруг Солнца, однако не смог
объяснить динамику этого движения.
После открытия Коперником гелиоцентрической системы мира начались
поиски закономерностей, которым подчиняется движение планет вокруг
Солнца.
Закон всемирного тяготения был установлен И. Ньютоном путем
обобщения результатов, получе6нных известными астрономами. Важную
роль сыграли закономерности движения планет, обнаруженные немецким
астрономом И. Кеплером (1571-1630) в результате обработки
астрономических наблюдений и информации датского астронома Тихо
Браге. Почему планеты обращаются вокруг солнца именно по таким
законам? На этот вопрос сумел ответить И.Ньютон, используя законы
движения, установленные Кеплером, и общие законы динамики.
Исаак Ньютон открыл этот закон в возрасте 23 лет, но целые 9 лет не
публиковал его, так как имевшиеся тогда неверные данные о
расстоянии между Землей и Луной не подтверждали его идею
IV. Закрепление
Как и во сколько раз изменится сила тяготения, если при неизменном расстоянии массы тел возрастут вдвое? (увеличится в 4 раза)
Как и во сколько раз изменится сила тяготения, если при неизменных массах тел расстояние между ними увеличится в 2 раза? В 3 раза? (уменьшится в 4 раза, в 9 раз).
***Подумай и ответь
V. Подведение итогов.
Рефлексия
VI. Домашнее задание. § . 15 упр 1,5
Урок 18.
Лабораторная работа №2 «Измерение ускорения свободного падания».
Цель работы: научиться измерять ускорение свободного падения, используя формулу периода колебаний математического маятника.
Приборы и материалы: штатив с муфтой и лапкой, шарик, прилепленный к нему нитью, секундомер, измерительная лента.
Правила техники безопасности.
На столе не должно быть никаких посторонних предметов. С металлическим шариком обращайтесь аккуратно!
Тренировочные задания и вопросы
1.Какое движение называют свободным падением?
2.Как экспериментально доказать, что ускорение свободного падения одинаково для всех тел в данной точке пространства?
3.От чего зависит ускорение свободного падения?
4.Выризите ускорение свободного падения из формулы периода колебаний математического маятника.
5.Выразите длину маятника из формулы периода колебаний математического маятника.
6.Как измениться период и частота колебаний нитяного маятника, если его поднять на высоту, равную радиусу Земли?
Порядок выполнения работы
1.Подвесьте к штативу шарик на нити. Измерьте длину математического маятника.
2.Отклоните маятник на 3-4 см от положения равновесия и отпустите его.
Измерьте время 20 полных колебаний маятника.
3.Измерьте время 3 раза. Найдите среднее значение времени как среднее арифметического.
Результаты измерений и вычислений с учетом погрешности измерений занести в таблицу.
Считайте, что погрешность измерения равна половине цены деления.
4.Определите период колебаний по формуле: Т=tср/N.
5.Из формулы периода колебаний математического маятника выразите ускорение свободного
падения и вычислите его по вашим данным.
6.Повторите измерения (п.1-5) изменив длину нити маятника.
7.Вычислите относительную и абсолютную погрешности измерения ускорения
свободного падения для каждого случая по формулам:
8.Запишите значение ускорения свободного падения в таблицу с учетом погрешности измерений.9.Все расчеты делаются под таблицей.
10 Сделайте соответствующие выводы.
Урок 19.
Ускорение свободного падения на Земле и других небесных телах.
Цель урока: Дать понятие ускорения свободного падения и сравнить с ускорением на других планетах.
Ход урока
I. Повторение. Проверка домашнего задания
- Что называется свободным падением тел?
- Что такое ускорение свободного падения?
- Почему в воздухе кусочек ваты падает с меньшим ускорением, чем железный шарик?
- Кто первым пришел к выводу о том, что свободное падение является равноускоренным движением?
- Действует ли сила тяжести на подброшенное вверх тело во время его подъема.
- С каким ускорением движется подброшенное вверх тело при отсутствии сопротивления воздуха. Как меняется при этом скорость движения тела?
- От чего зависит наибольшая высота подъема брошенного вверх тела в том случае, когда сопротивлением воздуха можно пренебречь?
II. Самостоятельная работа
I вариант
1. В трубке, из которой откачан воздух, на одной и той же высоте находятся дробинка, пробка и птичье перо. Какое из тел быстрее достигнет дна трубки?
а) дробинка;
б) пробка;
в) птичье перо;
г) все тела достигнут дна одновременно.
2. Чему равна скорость свободно падающего тела через 4 секунды? (v0 = 0 м/с, g = 10 м/с2)
а) 20 м/с;
б) 40 м/с;
в) 80 м/с;
г) 160 м/с.
3. Какой путь пройдет свободно падающее тело за 3 секунды? (v0 = 0 м/с,g = 10 м/с2)
а) 15 м;
б) 30 м;
в) 45 м;
г) 90 м.
4. Какой путь пройдет свободно падающее тело за пятую секунду? (v0 = 0 м/с, g = 10 м/с2)
а) 45 м;
б) 125 м;
в) 50 м;
г) 250 м.
5. Тело брошено вертикально вверх со скоростью 30 м/с. Чему равна максимальная высота подъема? (g = 10 м/с2)
а) 22,5 м;
б) 45 м;
в) 30 м;
г) 180 м.
II вариант
1. В трубке с воздухом при атмосферном давлении на одной и той же высоте находятся дробинка, пробка и птичье перо. Какое из этих тел быстрее достигает дна трубки при падении?
а) дробинка;
б) пробка;
в) птичье перо;
г) все тела достигнут дна одновременно.
2. Чему равна скорость свободно падающего тела через 3 секунды? (v0 = 0 м/с, g = 10 м/с2)
а) 15 м/с;
б) 30 м/с;
в) 45 м/с;
г) 90 м/с.
3. Какой путь пройдет свободно падающее тело за 4 секунды? (v0 = 0 м/с,g = 10 м/с2)
а) 20 м;
б) 40 м;
в) 80 м;
г) 160 м.
4. Какой путь пройдет свободно падающее тело за седьмую секунду? (v0 = 0 м/с, g = 10 м/с2)
а) 65 м;
б) 70 м;
в) 245 м;
г) 490 м.
5. Тело брошено вертикально вверх со скоростью 20 м/с. Чему равна максимальная высота подъема? (g = 10 м/с2)
а) 10 м;
б) 20 м;
в) 40 м;
г) 8 м.
II. Новый материал
Датский астроном Тихо Браге, многие годы наблюдая за движением планет, накопил многочисленные данные, но не сумел их обработать. Это сделал его ученик Иоганн Кеплер. Используя идею Коперника о гелиоцентрической системе и результаты наблюдений Тихо Браге, Кеплер установил законы движения планет вокруг Солнца. Но Кеплер не сумел объяснить динамику движения. Почему планеты обращаются вокруг Солнца именно по таким законам? На этот вопрос сумел ответить Исаак Ньютон, использую законы движения, установленные Кеплером, и общие законы динамики.
Ньютон предположил, что ряд явлений, казалось бы, не имеющих ничего общего (падение тел на Землю, обращение планет вокруг Солнца, движение Луны вокруг Земли, приливы и отливы и т. д.), вызваны одной причиной. Проведя многочисленные расчеты, Ньютон пришел к выводу, что небесные тела притягиваются друг к другу с силой, прямо пропорциональной произведению их масс и обратно пропорциональной квадрату расстояния между ними. Покажем, как Ньютон пришел к такому заключению.
Из второго закона динамики следует, что ускорение, которое получает тело под действием силы, обратно пропорционально массе тела. Но ускорение свободного падения не зависит от массы тела. Это возможно только в том случае, если сила, с которой Земля притягивает тело, изменяется пропорционально массе тела.
По третьему закону силы, с которыми взаимодействуют тела, равны. Если сила, действующая на одно тело, пропорциональна массе этого тела, то равная ей сила, действующая на второе тело, очевидно, пропорциональна массе второго тела. Но силы, действующие на оба тела, равны, следовательно, они пропорциональны массе и первого и второго тела.
Ньютон рассчитал отношение радиуса орбиты Луны к радиусу Земли. Отношение равнялось 60. А отношение ускорения свободного падения на Земле к центростремительному ускорению, с которым обращается вокруг Земли Луна, равнялось 3600. Следовательно, ускорение обратно пропорционально квадрату расстояния между телами.
Но по второму закону Ньютона сила и ускорение связаны прямой зависимостью, следовательно, сила обратно пропорциональна квадрату расстояния между телами.
Исаак Ньютон открыл этот закон в возрасте 23 лет, но 9 лет не публиковал, так как неверные данные о расстоянии между Землей и Луной не подтверждали его идею. И только когда было уточнено это расстояние, Ньютон в 1667 г. опубликовал закон всемирного тяготения.
Сила гравитационного взаимодействия двух тел (материальных точек) с массами m1 и m2 равна:
![]()
где G - гравитационная постоянная,
r - расстояние между телами. Гравитационная постоянная численно равна модулю силы тяготения, действующей на тело массой 1 кг со стороны другого тела такой же массы при расстоянии между телами равном 1 м.
Впервые гравитационная постоянная была измерена английским физиком Г. Кавендишем в 1788 г. с помощью прибора, называемого крутильными весами. Г. Кавендиш закрепил два маленьких свинцовых шара (диаметром 5 см и массой 775 г каждый) на противоположных концах двухметрового стержня. Стержень был подвешен на тонкой проволоке. Два больших свинцовых шара (20 см диаметром и массой 45,5 кг) близко подводились к маленьким. Силы притяжения со стороны больших шаров заставляли маленькие перемещаться, при этом проволока закручивалась. Степень закручивания была мерой силы, действующей между шарами. Эксперимент показал, что гравитационная постоянная G = 6,66 · 10-11 Н·м2/кг2.
Пределы применимости закона
Закон всемирного тяготения применим только для материальных точек, т. е. для тел, размеры которых значительно меньше, чем расстояния между ними; тел, имеющих форму шара; для шара большого радиуса, взаимодействующего с телами, размеры которых значительно меньше размеров шара.
Но закон неприменим, например, для взаимодействия бесконечного стержня и шара. В этом случае сила тяготения обратно пропорциональна только расстоянию, а не квадрату расстояния. А сила притяжения между телом и бесконечной плоскостью вообще от расстояния не зависит.
Сила тяжести
Частным случаем гравитационных сил является сила притяжения тел к Земле. Эту силу называют силой тяжести. В этом случае закон всемирного тяготения имеет вид:
![]()
где m - масса тела [кг],
М - масса Земли [кг],
R - радиус Земли [м],
h - высота над поверхностью [м].
Но сила тяжести FT = mg, отсюда ![]() a ускорение
свободного падения
a ускорение
свободного падения ![]()
На поверхности Земли (h = 0) ![]()
Ускорение свободного падения зависит
♦ от высоты над поверхностью Земли;
♦ от широты местности (Земля - неинерциальная система отсчета);
♦ от плотности пород земной коры;
♦ от формы Земли (приплюснута у полюсов).
В приведенной выше формуле для g последние три зависимости не учитываются. При этом еще раз подчеркнем, что ускорение свободного падения не зависит от массы тела.
Применение закона при открытии новых планет
Когда была открыта планета Уран, на основе закона всемирного тяготения рассчитали ее орбиту. Но истинная орбита планеты не совпала с расчетной. Предположили, что возмущение орбиты вызвало наличием еще одной планеты, находящейся за Ураном, которая своей силой тяготения изменяет его орбиту. Чтобы найти новую планету, необходимо было решить систему из 12 дифференциальных уравнений с 10 неизвестными. Эту задачу выполнил английский студент Адамс; решение он отправил в Английскую академию наук. Но там на его работу не обратили внимания. А французский математик Леверье, решив задачу, послал результат итальянскому астроному Галле. И тот, в первый же вечер наведя свою трубу в указанную точку, обнаружил новую планету. Ей дали название Нептун. Подобным же образом в 30-е годы двадцатого века была открыта и 9-я планета Солнечной системы - Плутон.
На вопрос о том, какова природа сил тяготения, Ньютон отвечал: «Не знаю, а гипотез измышлять не желаю».
III. Упражнения и вопросы для повторения
- Как формулируется закон всемирного тяготения?
- Какой вид имеет формула закона всемирного тяготения для материальных точек?
- Что называют гравитационной постоянной? Какой ее физический смысл? Каково значение в СИ?
- Что называется гравитационным полем?
- Зависит ли сила тяготения от свойств среды, в которой находятся тела?
- Зависит ли ускорение свободного падения тела от его массы?
- Одинакова ли сила тяжести в различных точках земного шара?
- Объясните влияние вращения Земли вокруг оси на ускорение свободного падения.
- Как изменяется ускорение свободного падения при удалении от поверхности Земли?
- Почему Луна не падает на Землю? (Луна обращается вокруг Земли, удерживаемая силой притяжения. Луна не падает на Землю, потому что, имея начальную скорость, движется по инерции. Если прекратится действие силы притяжения Луны к Земле, Луна по прямой линии умчится в бездну космического пространства. Прекратись движение по инерции - и Луна упала бы на Землю. Падение продолжалось бы четверо суток девятнадцать часов пятьдесят четыре минуты семь секунд. Так рассчитал Ньютон.)
IV. Решение задач
Задача 1
На каком расстоянии сила притяжения двух шариков массами по 1 г равна 6,7 · 10-17 Н? (Ответ: R ≈ 1м.)
Задача 2
На какую высоту от поверхности Земли поднялся космический корабль, если приборы отметили уменьшение ускорения свободного падения до 4,9 м/с2? (Ответ: h = 2600 км.)
Задача 3
Сила тяготения между двумя шарами 0,0001 Н. Какова масса одного из шаров, если расстояние между их центрами 1 м, а масса другого шара 100 кг? (Ответ: примерно 15 тонн.)
Домашнее задание
1. Выучить § 15, 16;
Урок 20.
Прямолинейное и криволинейное движение. Движение по окружности с постоянной по модулю скорости.
Цели урока:
Рассмотреть особенности криволинейного движения и, в частности, движения по окружности. Ввести понятия центростремительного ускорения и периода обращения.
Ход урока
I. Повторение. Проверка домашнего задания
Устный опрос:
- Что было названо всемирным тяготением?
- Как иначе называются силы всемирного тяготения?
- Кто открыл закон всемирного тяготения?
- Как читается закон всемирного тяготения?
- Запишите формулу, выражающую закон всемирного тяготения. В каких случаях можно применять эту формулу?
- Притягивается ли Земля к висящему на ветке яблоку?
- Верно ли, что притяжение тел к Земле является одним из примеров всемирного тяготения?
- Как меняется сила тяжести, действующая на тело, при его удалении от поверхности Земли?
- В каком случае сила тяжести, действующая на одно и то же тело, будет больше: если это тело находится в экваториальной области Земли или на одном из полюсов? Почему?
- Что вы знаете об ускорении свободного падения на Луне? Сравните gз иgл.
Письменная проверочная работа
1. Какая из приведенных ниже формул выражает закон всемирного тяготения?

д) среди ответов правильного ответа нет.
2. Космический корабль удаляется от Земли. Как изменится сила тяготения, действующая со стороны Земли на ракету, при увеличении расстояния до центра Земли в 2 раза?
а) не изменится;
б) уменьшится в 2 раза;
в) увеличится в 2 раза;
г) уменьшится в 4 раза;
д) увеличится в 4 раза.
3. Вокруг планеты массой М движется спутник массой m. Какое утверждение о силе гравитационного притяжения, действующего со стороны планеты на спутник, правильно?
а) прямо пропорциональна массе М и не зависит от массы m;
б) прямо пропорциональна массе m и не зависит от М;
в) прямо пропорциональна произведению масс m · М;
г) прямо пропорциональна частному масс;
д) не зависит ни от М, ни от m.
4. При свободном падении с крыши дома целого кирпича он долетает до Земли за 2 с. Сколько времени будет длиться падение с той же крыши половинки кирпича?
а) 2 с;
б) 4 с;
в) ![]() с;
с;
г) 1 с.
5. Масса Луны примерно в 81 раз меньше массы Земли. Чему равно отношение силы всемирного тяготения F1, действующей со стороны Земли на Луну, и силе F2, действующей со стороны Луны на Землю?
а) 1/81;
б) 1/9;
в) 1;
г) 9;
д) 81.
II. Новый материал
В природе и в технике очень часто встречаются движения, траектории, которых представляют собой не прямые, а кривые линии. Это криволинейное движение. По криволинейным траекториям движутся в космическом пространстве планеты и искусственные спутники Земли, а на Земле - всевозможные средства транспорта, части машин и механизмов, воды рек, воздух атмосферы и т. д.
Если прижать к вращающемуся точильному камню конец стального прутика, то раскаленные частицы, отрывающиеся от камня, будут видны в виде искр. Эти частицы летят с той скоростью, которой они обладали в момент отрыва от камня. Хорошо видно, что направление движения искр совпадает с касательной к окружности в той точке, где пруток касается камня (рис. 36). По касательной движутся брызги от колес буксующего автомобиля.
Таким образом, мгновенная скорость тела в разных точках криволинейной траектории имеет различное направление. По модулю же скорость может быть всюду одинакова или изменяться от точки к точке.
Но даже, если модуль скорости не изменяется, ее нельзя считать постоянной. Скорость - векторная величина. Для векторной величины модуль и направление одинаково важны. Криволинейное движение - это всегда движение с ускорением, даже если по модулю скорость постоянная.
Итак, пусть у нас есть некоторая сложная криволинейная траектория (рис. 37).
Из рисунка видно, что отдельные части криволинейной траектории представляют собой приблизительно дуги окружностей. Выходит, что движение по любой криволинейной траектории можно представить как движение по дугам некоторых окружностей. Поэтому задача поиска ускорения при равномерном криволинейном движении сводится к отысканию ускорения при равномерном движении тела по окружности.
Ускорение тела, равномерно движущегося по окружности, в любой, точке центростремительное, т. е. направлено по радиусу окружности к ее центру. В любой точке вектор ускорения перпендикулярен вектору скорости (рис. 38).
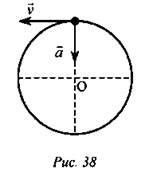
Модуль центростремительного ускорения ![]() где v - линейная
скорость тела, a R - радиус окружности.
где v - линейная
скорость тела, a R - радиус окружности.
Движение по окружности часто характеризуют не скоростью
движения, а промежутком времени, за который тело совершает один
полный оборот. Это величина называется периодом обращения и
обозначается буквой Т. Найдем связь между периодом обращения Т и
модулем скорости при равномерном движении по окружности радиуса R.
Т. к. ![]() а
путь S равен длине окружности: S = 2πR , то
а
путь S равен длине окружности: S = 2πR , то ![]()
Движение тела по окружности можно охарактеризовать еще одной величиной - числом оборотов в единицу времени. Ее называют частотой обращения η:
![]()
Единицей измерения частоты [η] = с-1 = Гц.
III. Упражнения и вопросы для повторения
- Как направлена мгновенная скорость при криволинейном движении?
- Что называется линейной скоростью тела при его движении по окружности?
- Что называется периодом и частотой обращения.
- Как эти величины связаны между собой?
- Как направлено ускорение тела, движущегося по окружности с постоянной по модулю скоростью?
- Можно ли считать центростремительное ускорение постоянным, а равномерное движение по окружности равноускоренным?
- Если при движении тела по окружности модуль скорости изменяется, будет ли ускорение тела направлено к центру окружности?
IV. Решение задач
1. Точильный круг радиусом 10 см делает один оборот за 0,2 с. Найдите скорость точек, наиболее удаленных от оси вращения. (Ответ: 3,1 м/с.)
2. Автомобиль движется по закруглению дороги радиусом 100 м. Чему равно центростремительное ускорение автомобиля, если он движется со скоростью 54 км/ч? (Ответ: а = 2,25 м/с2.)
3. Какова скорость движения автомобиля, если его колеса радиусом 30 см делают 600 оборотов в минуту? (Ответ: примерно 19 м/с.)
4. Период обращения первого космического корабля - спутника Земли «Восток» равнялось 90 минут. Средняя высота спутника над Землей была равна 320 км. Радиус Земли 6400 км. Вычислить скорость корабля. (Ответ: v= 7,8 км/с.)
Домашнее задание
1. Выучить § 17, 18;
Урок 21.
Решение задач по теме: «Закон Всемирного тяготения»
Цели урока:
Образовательные:
Закрепить знания по предыдущим темам.
Закрепить навыки решения задач (расчетных, качественных, экспериментальных).
Совершенствовать навыки применения формул.
Повторить основные физические понятия по данной теме.
Научить применять знания, полученные на уроке.
Показать связь с жизнью, расширять межпредметные связи.
Воспитательные:
Воспитывать добросовестное отношение к учебе.
Прививать навыки как самостоятельной работы, так и работы в коллективе.
Воспитывать познавательную потребность и интерес к предмету.
Формировать интерес к предмету, к учебе, воспитывать инициативу, творческое отношение.
Содействовать формированию представлений об общей физической картине мира.
Показать объективный характер законов природы.
Развивающие:
Развивать способность быстро воспринимать информацию и выполнять необходимые задания.
Развивать физическое мышление учащихся, их творческие способности.
Расширять познавательный интерес путем привлечения дополнительного материала, а также потребности к углублению и расширению знаний.
Ход урока
Учитель: Здравствуйте, дети, садитесь. Сегодня на уроке мы с вами повторим основные физические понятия, закрепим знания, полученные на предыдущих уроках, попробуем объяснить явления, которые происходят в природе, научимся применять знания, полученные ранее, закрепим навыки решения задач.
Зачем вообще изучается любая наука? Чтобы применять полученные знания на практике. В жизни проблемы возникают все время, и мы их все время решаем. Вот, например, проблема: как использовать свободное время?
Дети рассуждают.
Учитель: Появляется цепочка действий: проблема - идея - расчеты - практика. Их всегда проходит человек, решая возникшие перед ним в жизни задачи. Мы изучили законы Ньютона и закон всемирного тяготения. Давайте вспомним их:
Как читается первый закон Ньютона?
Ученик: Существуют такие системы отсчета, относительно которых тела сохраняют свою скорость неизменной, если на них не действуют другие тела.
Учитель: Как читается второй закон Ньютона?
Ученик: Ускорение тела прямо пропорционально равнодействующей сил, приложенных к телу, и обратно пропорционально его массе.
Учитель: Сформулируйте третий закон Ньютона?
Ученик: Силы, с которыми два тела действуют друг на друга, равны по модулю и противоположны по направлению.
Учитель: Чему равна гравитационная постоянная?
Ученик: G = 6,67·10-11 Н*м2 /кг2.
Учитель: Про гравитационную постоянную есть даже стихотворение Е.Ефимовского:
Удивительный и странный
По устройству мир земной!
Во всемирной постоянной
Смысл содержится простой:
Притяжения здесь сила
Для двух тел отражена,
Килограмм у каждой было,
Между ними - метр длина.
В каком году открыт закон всемирного тяготения?
Ученик: 1667 году.
Учитель: А теперь переходим к решению задач.
Разминочные задачи.
Притягивается ли к Луне человек, стоящий на Земле? К чему он притягивается сильнее: к Луне или к Земле? Притягивается ли Луна к этому человеку?
Ученик: Да, притягивается. Притягивается сильнее к Земле, так как расстояние меньше. Луна притягивается к человеку.
Как и во сколько раз изменится сила тяготения, если при неизменном расстоянии массы тел возрастут вдвое?
Ученик: Увеличится в 4 раза.
Как и во сколько раз изменится сила тяготения, если при неизменных массах тел расстояние между ними увеличится в 2 раза?
Ученик: Уменьшится в 4 раза
Что притягивает к себе с большей силой: Земля - Луну или Луна - Землю?
Ученик: Одинаково.
Самый крупный камень, извлеченный хирургом из желчных путей человека, имел массу 6,29 кг. Какую силу приложил врач при его подъёме?
Ученик: 63 Н.
Самая тяжелая свинья, выращенная в США в 1933 году, имела массу 1157, 5 кг. Сколько человек потребуется, чтобы поднять её на весы, если каждый человек разовьет усилие 500 Н?
Ученик: 23 человека.
В 1987 году механизатор нашел в борозде золотой слиток объемом 665,2 см3 и плотностью 19320 кг/м3. Какая сила понадобилась ему, чтобы поднять слиток с земли?
Ученик: 126 Н.
Пусть между двумя деревянными шарами, что лежат на столе, сила тяготения равна F. Изменится ли численное значение этой силы, если между шарами поместить экран?
Ученик: Нет.
С какой силой притягиваются друг к другу две книги массой 0,2 кг каждая, находящиеся на расстоянии 1 м друг от друга?
Ученик: 0,26*10-11Н
Солнце притягивает Луну почти в два раза сильнее, чем Земля. Почему же мы до сих пор "не потеряли" Луну?
Ответ ученика.
Между какими двумя из трех шаров сила тяготения наибольшая?
При облете вокруг Земли "Аполлон - 13" был на максимальной высоте 400,187 км, а при облете Луны - на высоте 254 км. Как отличались силы притяжения объекта к небесным телам?
Ученик: Сила притяжения зависит от расстояния между телами и их масс. Земля по массе больше, поэтому сила притяжения больше, чем у Луны.
Практическое задание: на столе на штативе висит на нити груз массой 200 г. Вычислите силу всемирного тяготения.
Упражнение 16 (1) из учебника (работа с учебником).
Учитель: А теперь мы немного отдохнем.
Физкультминутка.
Давайте, изобразим:
Тела падают, (руки - вверх, вниз).
Приливы и отливы (руки - вправо, влево)
Движение Луны вокруг Земли (круговые движения руками).
Притяжение друг к другу.
Гравитационная постоянная открыта Генри Кавендишем - богатым английским лордом. Если бы эта величина была бы в 100 раз больше, то это привело бы к тому, что время существования звезд уменьшилось (и Солнца в том числе), и разумная жизнь на Земле появиться не успела. Нас бы с вами не было сейчас.
В результате открытия Ньютона выяснилось, что множество, казалось бы, разнородных явлений: падение тел на Земле, видимые движения Луны и Солнца, отливы и приливы - это проявление закона всемирного тяготения.
Всемирное тяготение, и только оно, объясняет устойчивость Солнечной системы, движение планет и других тел. Луна движется по орбите силами притяжения Земли, Земля удерживается на своей траектории силами притяжения солнца. С помощью закона всемирного тяготения открыты планеты Уран и Нептун. Поэтому говорят об этих планетах, что они открыты на "кончике пера". Благодаря закону всемирного тяготения точно определяют место солнечных и лунных затмений.
g= G Mз/ Rз2 - доказал Кавендиш, который после этого с гордостью заявил, что "взвесил Землю".
Учитель: Чтобы вы сделали, если вам на голову упадет яблоко?
Ответы учеников.
Учитель: А Ньютон не стал есть яблоко, а задумался и открыл закон всемирного тяготения.
Посмотрите на модель Солнечной системы, вот так движутся планеты вокруг Солнца. И движение планет подчиняется закону всемирного тяготения. Поэтому Земля "не уходит" от Солнца. Между нами тоже существует тяготение.
Почему мы не замечаем притяжения на поверхности Земли, хотя говорим, что сила тяготения - всемирная? Чтобы ответить на этот вопрос, рассчитаем силу притяжения между двумя учениками, сидящими за одной партой.
Ученики рассчитывают самостоятельно.
Вывод: эта сила не разорвет даже тончайшей паутинки. Может ли она быть замечена? (Ответы учеников).
Учитель: У многих авторов встречаются научные ошибки, неточности в художественной литературе. Например, Маленький принц (Экзюпери), живший на своей планете, мог поместиться только один сам? Что случится, если сила тяготения исчезнет?
Обсуждение.
Учитель: Это была бы ужасная катастрофа! Все полетело бы кувырком. Как у Чуковского:
Что такое, что случилось?
Отчего же все кругом
Завертелось, закружилось
И помчались колесом?
Утюги за сапогами,
Сапоги за пирогами,
Пироги за утюгами,
Кочерга за кушаком -
Все вертится и кружится,
И несется кувырком.
Несмотря на справедливость и огромное практическое значение закона, остается нерешенным вопрос: какими причинами вызывается гравитационное взаимодействие всех тел. Сам Ньютон говорил: "Не знаю, а гипотез не измышляю". Окончательно эта загадка не разгадана и сегодня.
Поставить оценки учащимся.
Спасибо за урок.
Домашнее задание параграф 18 повторить
Урок 22.
Искусственные спутники Земли
Цель урока:
Объяснить значение первой космической скорости, научить ее находить.
Ход урока
I. Повторение. Проверка домашнего задания
-
С помощью какого опыта можно убедиться в том, что мгновенная скорость тела, движущегося по окружности, в любой точке этой окружности направлена по касательной к ней?
-
Куда направлено ускорение тела при его движении по окружности с постоянной по модулю скоростью? Как называется это ускорение?
-
По какой формуле можно вычислить модуль вектора центростремительного ускорения?
II. Письменная проверочная работа
Вариант I
1. Тело движется равномерно по окружности в направлении по часовой стрелке (рис. 39). Как направлен вектор ускорения при таком движении?
а) 1;
б) 2;
в) 3;
г) 4.
2. Автомобиль движется на повороте по круговой траектории радиусом 50 м с постоянной по модулю скоростью 10 м/с. Каково ускорение автомобиля?
а) 1 м/с2;
б) 2 м/с2;
в) 5 м/с2;
г) 0 м/с2.
3. Тело движется по окружности радиусом 10 м. Период его обращения равен 20 с. Чему равна скорость тела?
а) 2 м/с;
б) π м/с;
в) 2π м/с;
г) 4π м/с.
4. Тело движется по окружности радиусом 5 м со скоростью 20 м/с. Чему равна частота обращения?
а) 2/π с-1;
б) 2π с-1;
в) 2π2 с-1;
г) 0,5 с-1.
5. Две материальные точки движутся по окружности с радиусами R1 = R иR2 = 2R c одинаковыми скоростями. Сравните их центростремильные ускорения.
а) а1 = а2;
б) а1 = 2а2;
в) а1 = a2/2;
г) а1 = 4а2.
6. Автомобиль движется с постоянной по модулю скоростью по траектории представленной на рисунке 40. В какой из указанных точек траектории центростремительное ускорение минимально?
а) 1;
б) 2;
в) 3;
г) во всех точках одинаково.
Вариант II
1. Тело движется равномерно по окружности в направлении против часовой стрелки (рис. 41). Как направлен вектор ускорения при таком движении?
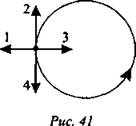
а) 1;
б) 2;
в) 3;
г) 4.
2. Скорость крайних точек точильного круга радиусом 10 см равна 60 м/с. Чему равно их центростремительное ускорение?
а) 6 м/с2;
б) 360 м/с2;
в) 3600 м/с2;
г) 36000 м/с2.
3. Тело движется по окружности радиусом 5 м. Период его обращения равен 10 с. Чему равна скорость тела?
а) 4π м/с;
б) 2π м/с;
в) π м/с;
г) 2 м/с.
4. Тело движется по окружности радиусом 3 м со скоростью 12 м/с. Чему равна частота обращения?
a) 0,5 с-1;
б) 2 с-1;
в) 2/π с-1;
г) 2π2 с-1.
5. Две материальные точки движутся по окружности с радиусами R1 = R иR2 = 2R с одинаковыми периодами. Сравните их центростремильные ускорения.
а) а1 = а2.
б) а1 = 2а2
в) а1 = а2/2;
г) а1 = а2/4.
6. Автомобиль движется с постоянной по модулю скоростью по траектории представленной на рисунке 42. В какой из указанных точек траектории центростремительное ускорение максимально?
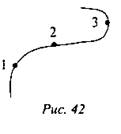
а) 1;
б) 2;
в) 5;
г) во всех точках одинаково.
II. Новый материал
Прежде чем приступить к изучению нового материала, ответьте на несколько вопросов:
-
Какая планета называется «Голубой»? (Земля.)
-
Когда был запущен первый искусственный спутник? (4 октября 1957 г.)
-
Кто первый космонавт Земли? (Ю. А. Гагарин, 12 апреля 1961 г.)
-
Кто первым ступил на Луну? (Нил Армстронг, США.)
Для того чтобы появились эти вопросы, нужно задать главный вопрос: Что нужно сделать, чтобы тело стало искусственным спутником Земли?
Если бросить тело с некоторой высоты, сообщив телу скорость v0 в горизонтальном направлении, то тело упадет, двигаясь по траектории, вид которой парабола. Это в том случае, если поверхность Земли плоская, что допустимо при небольших скоростях тела и сравнительно небольших расстояниях.
В действительности же Земля - шар, и с продвижением тела по его траектории поверхность Земле несколько удаляется от него. Можно подобрать такое значение скорости тела v0, при котором поверхность Земли (из-за ее кривизны) будет удаляться от тела как раз на столько, на сколько тело приблизится к Земли, благодаря притяжению к ней. В этом случае тело будет двигаться на постоянном расстоянии h от поверхности Земли, т. е. по окружности радиуса (R3 + h).
Вычислим, какой скоростью должен обладать искусственный спутник Земли, чтобы он двигался по круговой орбите на высоте h над поверхностью Земли. На больших высотах воздух сильно разряжен и оказывает незначительное сопротивление движущимся телам. Будем считать, что на спутник действует только гравитационная сила, направленная к центру Земли.
![]()
где М - масса Земли, m - масса спутника.
Эта сила сообщает спутнику центростремительное ускорение
![]()
Но по второму закону Ньютона: ![]()
Отсюда: ![]() т. е.
т. е. ![]()
Из формулы видно, что: а) скорость спутника зависит от его высоты над поверхностью Земли; б) скорость не зависит от массы спутника.
Спутником может стать любое тело, если ему сообщить на данной высоте необходимую скорость, направленную перпендикулярно радиусу Земли.
Скорость, которую необходимо сообщить телу, чтобы оно стало спутником планеты, называется первой космической скоростью.
У поверхности Земли при h = 0, тогда  Т. к. на
поверхности Земли ускорение свободного падения
Т. к. на
поверхности Земли ускорение свободного падения ![]() то
то ![]()
Такую огромную скорость могут развить только мощные космические ракеты. В настоящее время вокруг Земли обращаются тысячи искусственных спутников. Руками человека за последние годы создавались и искусственные спутники Луны, планет Венера и Марс, а также Солнца.
III. Закрепление изученного
- Как должна быть направлена скорость тела в момент его выхода на круговую орбиту, чтобы оно стало искусственным спутником Земли?
- Что такое первая космическая скорость? Чему она равна для Земли?
- Можно ли считать движение искусственного спутника Земли равноускоренным?
IV. Решение задач
1. Вычислите период обращения спутника Земли на высоте 300 км. (Ответ: Т = 90 мин.)
2. На какой высоте над поверхностью Земли должен быть запущен спутник, чтобы период его обращения по орбите был равен 24 ч? (Ответ: 36000 км.)
3. Вычислите первую космическую скорость для высоты над Землей, равной радиусу Земли. (Ответ: 5,59 км/с.)
Домашнее задание
1. Выучить § 19
Урок 23.
Импульс. Закон сохранения импульса
Цели урока: Дать понятие импульса тела; изучить закон сохранения импульса. Учиться решать задачи.
Ход урока
I. Повторение. Проверка домашнего задания
- Приведите примеры (из области астрономии), доказывающие, что при отсутствии сил сопротивления тело может неограниченно долго двигаться по замкнутой траектории под действием силы, меняющей направление скорости движения этого тела.
- Почему спутники, обращаясь вокруг Земли под действием силы тяжести, не падают на Землю?
- Можно ли считать обращение спутника вокруг Земли свободным падением?
- Что надо сделать с физическим телом, чтобы оно стало искусственным спутником Земли?
- Выведите формулу для расчета первой космической скорости спутника, движущегося по круговой орбите вблизи поверхности Земли.
- Как движется спутник, обладающий первой космической скоростью? Второй космической скоростью?
- От чего зависит первая космическая скорость?
Решения домашних задач разбираются на доске.
II. Понятие импульса
В самом начале урока учитель демонстрирует несколько опытов упругого столкновения двух шаров разной массы. Можно продемонстрировать, как начинает двигаться изначально неподвижная тележка, если на нее бросить деревянный или металлический брусок.
- Как описать взаимодействие тел в данных опытах?
- Удобно ли использовать для этого законы Ньютона?
Найдем взаимосвязь между действующей на тело силой ![]() , временем ее
действия t, и изменением скорости тела.
, временем ее
действия t, и изменением скорости тела.
Пусть на тело массой m, которое покоится (v0 = 0),
начинает действовать сила ![]() . Тогда из второго закона
Ньютона ускорение этого тела будет
. Тогда из второго закона
Ньютона ускорение этого тела будет ![]() . Причем:
. Причем:
![]()
С другой стороны:
![]()
или:
![]()
Обозначим произведение ![]() через
через ![]() :
: ![]()
Произведение массы тела на его скорость называется импульсом
тела. Понятие импульса первым ввел Декарт. Правда, величину
![]() он
назвал «количеством движения». Слово «импульс» в переводе с
латинского означает «толчок».
он
назвал «количеством движения». Слово «импульс» в переводе с
латинского означает «толчок».
Импульс ![]() - векторная величина. Он
всегда совпадает по направлению с вектором скорости тела. Любое
тело, которое движется, обладает импульсом.
- векторная величина. Он
всегда совпадает по направлению с вектором скорости тела. Любое
тело, которое движется, обладает импульсом.
Как любая физическая величина, импульс измеряется в определенных единицах:
![]()
Если тело массой 1 кг движется со скоростью 1 м/с, это значит, что его импульс равен 1 кг·м/с или 1 Н·с.
Получив формулу ![]() и введя понятие «импульс
тела», ничего не было сказано о смысле левой части. В то же
время, ученики часто спрашивают о смысле левой части равенства.
Можно объяснить, что в физике произведение силы на время действия
называют импульсом силы. Импульс силы всегда показывает, как
изменяется импульс тела за данное время.
и введя понятие «импульс
тела», ничего не было сказано о смысле левой части. В то же
время, ученики часто спрашивают о смысле левой части равенства.
Можно объяснить, что в физике произведение силы на время действия
называют импульсом силы. Импульс силы всегда показывает, как
изменяется импульс тела за данное время.
Если же начальная скорость v0 ≠ 0, тогда с учетом,
что ![]() получим:
получим:
![]()
Этот закон зачастую называют II законом Ньютона в импульсной форме.
III. Закон сохранения импульса
При взаимодействии тел их импульсы могут изменяться.
Эксперимент 1
На нитях подвешиваются два шарика (см. рис. 43).
Правый отклоняют и отпускают. Вернувшись в прежнее положение и ударившись о неподвижный шарик, он останавливается. При этом левый шарик приходит в движение и отклоняется практически на тот же угол, что и отклоняли правый шар.
Импульс обладает интересным свойством, которое есть лишь у немногих физических величин. Это свойство сохранения. Но закон сохранения импульса выполняется только в замкнутой системе.
Система тел называется замкнутой, если взаимодействующие между собой тела, не взаимодействуют с другими телами.
Тогда для двух взаимодействующих тел:
![]() т. е.:
т. е.:
![]()
Таким образом:
Геометрическая сумма импульсов тел, составляющих замкнутую систему, остается постоянной при любых движениях и взаимодействиях тел системы.
Примеры: ружье и пуля в его стволе, пушка и снаряд, оболочка ракеты и топливо в ней и т. д.
IV. Закрепление изученного
- Что называется импульсом тела?
- Запишите формулу импульса тела.
- Запишите формулу импульса силы.
- Какова единица измерения импульса тела в СИ?
- Что такое замкнутая система тел?
- Какую систему тел называют незамкнутой?
- На примере взаимодействия двух тел в замкнутой системе покажите, как устанавливают закон сохранения импульса.
V. Решение задач
Задача 1
На неподвижную тележку массой 100 кг прыгает человек массой 50 кг со скоростью 6 м/с. С какой скоростью начнет двигаться тележка с человеком?
Дано:
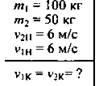
Решение:
По закону сохранения импульса в замкнутой
системе «человек- тележка» имеем: ![]() , или
, или ![]()
Т. к. v1H = 0 (тележка покоится), a
v1K = v2K (человек движется вместе с
тележкой), то получим: ![]()
Очевидно, что направления скоростей ![]() совпадают.
совпадают.
Тогда для модулей имеем: ![]()
Откуда конечная скорость ![]()
Ответ: v1 = 2 м/с
Задача 2
Орудие, не имеющее противооткатного устройства, стреляет снарядом под углом α = 60° к горизонту. Масса снаряда m1 = 10 кг, его начальная скоростьv1 = 500 м/с. Какова скорость отката орудия, если его масса m2 = 500 кг? (Ответ: 5 м/с.)
Задача 3
Найти импульса грузового автомобиля массой 10 т, движущегося со скоростью 36 км/с, и легкового автомобиля массой 1 т, движущегося со скоростью 25 м/с. (Ответ: p1 = 105 кг·м/с, р2 = 25 · 103 кг·м/с.)
Домашнее задание
1. Выучить § 21, 22;
2. Выполнить упражнения 20,21 (2);
3. Решить задачу: Тело массой m = 100 г брошено вертикально вверх со скоростью v0 = 20 м/с. Пренебрегая сопротивлением воздуха, изобразите графически, как изменяется модуль импульса тела во время полета.
Урок 24.
Решение задач по теме «Импульс. Закон сохранения импульса»
Цели урока:
Научить учащихся применять теоретические знания при решении задач.
Ход урока
I. Повторение. Проверка домашнего задания
-
- Что называется импульсом тела?
-
- Что можно сказать о направлениях векторов импульса и скорости движущегося тела.
-
- Что принимают за единицу импульса?
-
- Что означает утверждение о том, что несколько тел образуют замкнутую систему?
-
- Сформулируйте закон сохранения импульса.
-
- Для замкнутой системы, состоящей из двух тел, запишите закон сохранения импульса. Поясните, что означает каждый символ в этом уравнении.
II. Решение задач
Задача 1
Движение материальной точки описывается уравнением: х = 5 · 8t + 4t2. Приняв ее массу равной 2 кг, найти импульс через 2 с и через 4 с после начала отсчета времени, а также силу, вызвавшую это изменение импульса. (Ответ: р1 = 16 кг·м/с, р2 = 48 кг·м/с, F = 16 Н.)
Задача 2
Снаряд массой 100 кг, летящий горизонтально вдоль железнодорожного пути со скоростью 500 м/с, попадает в вагон с песком массой 10 т и застревает в нем. Найти скорость вагона, если он двигается со скоростью 36 км/ч навстречу снаряду. (Ответ: vx = -5 м/с.)
Знак «-» в ответе показывает, что вагон движется в направлении, противоположном оси ОХ, то есть направление движения вагона изменилось.
Задача 3
Тело массой 0,2 кг падает с высоты 1 м с ускорением 8 м/с2. Найти изменение импульса тела за время полета. (Ответ: 0,8.)
Задача 4
Снаряд массой 40 кг, летящий в горизонтальном направлении со скоростью 600 м/с, разрывается на две части с массами 30 кг и 10 кг. Большая часть стала двигаться в прежнем направлении со скоростью 900 м/с. Определить величину и направление скорости меньшей части снаряда. (Ответ: v2 = 300 м/с.)
Задача 5
Тележка с песком катится со скоростью v1 = 1 м/с по горизонтальной поверхности без трения. Навстречу тележке летит шар массой m = 3 кг со скоростью v2 = 8 м/с, направленной под углом α = 60° к горизонту. После встречи с тележкой шар застревает в песке. С какой скоростью и в какую сторону покатится тележка после встречи с шаром? Масса тележки с песком М = 10 кг. (Ответ: vx = -0,15 м/с, тележка с песком поедет в обратном направлении.)
Задача 6
В результате взрыва камень разлетелся на три части. Два куска летят под прямым углом друг к другу: кусок массой m1 = 1 кг со скоростью v1 = 12 м/с, кусок массой m2 = 2 кг со скоростью v2 = 8 м/с. Третий кусок отлетает со скоростью v3 = 40 м/с. Какова его масса и в каком направлении он летит? (Ответ: угол примерно равен 53°, m3 = 0,5 кг.)
Вариант I
1. Каким выражением определяют импульс тела?

2. В каких единицах измеряется импульс в Международной системе?
а) 1 Н;
б) 1 кг;
в) 1 Н·c;
г) 1 Дж.
3. Чему равно изменение импульса тела, если на него подействовала сила 15 Н в течение 5 с?
а) 3 кг·м/с;
б) 5 кг·м/с;
в) 15 кг·м/с;
г) 75 кг·м/с.
4. Тело массой m движется со скоростью v. После взаимодействия со стенкой тело стало двигаться в противоположном направлении с той же по модулю скоростью. Чему равен модуль изменения импульса тела?
а) 0;
б) mv;
в) 2 mv;
г) 4 mv.
5. Два автомобиля с одинаковыми массами m движутся со скоростями v и 3v относительно Земли в противоположных направлениях. Чему равен импульс второго автомобиля в системе отчета, связанной с первым автомобилем?
a) mv;
б) mv;
в) 3 mv;
г) 4 mv.
6. На рис. 44 представлен график зависимости модуля силы F, действующей на тело, от времени. Чему равно изменение скорости тела массой 2 кг за 4 с?
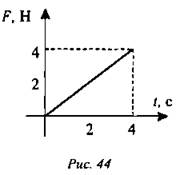
а) 4 м /с;
б) 8 м/с;
в) 16 м/с;
г) 32 м/с.
7. Какое из выражений соответствует закону сохранения импульса для случая взаимодействия двух тел?
8. Железнодорожный вагон массой m, движущийся со скоростью v, сталкивается с неподвижным вагоном массой 2m и сцепляется с ним. Каким суммарным импульсом обладают два вагона после столкновения?
а) 0;
б) mv;
в) 2 mv;
г) 3 mv.
9. Тележка массой 2 кг, движущаяся со скоростью 3 м/с, сталкивается с неподвижной тележкой массой 4 кг и сцепляется с ней. Чему равна скорость обоих тележек после взаимодействия?
а) 0,5 м/с;
б) 1 м/с;
в) 1,5 м/с;
г) 3 м/с.
10. Скорость легкового автомобиля в 3 раза больше скорости грузового, а масса грузового - в 6 раз больше легкового. Сравните модули импульсов легкового p1, и грузового р2автомобилей.
а) р1 = p2;
б) р2 = 2р1;
в) p2 = 2p1;
г) р2 = 4р1.
11. При выстреле из пистолета вылетает пуля массой т со скоростью v. Какую по модулю скорость приобретает после выстрела пистолет, если его масса в 100 раз больше массы пули?
a) 0;
б) v/100;
b) v;
г)100v.
12. На одном конце неподвижной длинной тележки массой m1 стоит мальчик массой m2. С какой скоростью будет двигаться тележка, если мальчик побежит со скоростью v относительно тележки?
![]()
Вариант II
1. Чему равен импульс тела массой 2 кг, движущегося со скоростью 3 м/с?
а) 1,5 кг·м/с;
б) 6 кг·м/с;
в) 9 кг·м/с;
г) 18 кг·м/с.
2. Каково наименование единицы импульса, выраженное через основные единицы Международной системы?
а) 1 кг;
б) 1 кг·м/с;
в) 1 кг·м/с2;
г) 1 кг·м2/с2.
3. Каким выражением определяют импульс тела?

4. Тело массой 2 кг движется со скоростью 3 м/с. После взаимодействия со стенкой тело стало двигаться в противоположном направлении со скоростью 2 м/с. Чему равен модуль изменения импульса тела?
а) 2 кг·м/с;
б) 4 кг·м/с;
в) 6 кг·м/с;
г) 10 кг·м/с.
5. Два автомобиля с одинаковыми массами m движутся со скоростями v и 3v относительно Земли в одном направлении. Чему равен импульс второго автомобиля в системе отчета, связанной с первым автомобилем?
a) mv;
б) 2 mv;
в) 3 mv;
г) 4 mv.
6. На рис. 45 представлен график зависимости модуля силы F, действующей на тело, от времени. Чему равно изменение скорости тела массой 2 кг за 3 с?
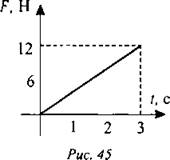
а) 9 м/с;
б) 12 м/с;
в) 18 м/с;
г) 36 м/с.
7. Какое из выражений соответствует закону сохранения импульса для случая взаимодействия двух тел?
8. Тележка массой 3 кг, движущаяся со скоростью 4 м/с, сталкивается с неподвижной тележкой массой той же массы и сцепляется с ней. Чему равен импульс тележек после взаимодействия?
а) 6 кг·м/с;
б) 12 кг·м/с;
в) 24 кг·м/с;
г) 0.
9. Тележка массой 3 кг, движущаяся со скоростью 4 м/с, сталкивается с неподвижной тележкой той же массы и сцепляется с ней. Чему равна скорость обеих тележек после взаимодействия.
а) 2 м/с;
б) 3 м/с;
в) 4 м/с;
г) 12 м/с.
10. Скорость легкового автомобиля в 4 раза больше скорости грузового, а масса грузового - в 2 раза больше массы легкового. Сравните значения модулей импульсов легкового p1 и грузового р2 автомобилей.
а) p1 = p2
б) p1 = 2p2;
в) P2 = 2p1;'
г) p1 = 4р2.
1
2
3
4
5
6
7
8
9
1
б
в
г
в
г
а
в
б
б
в
б
а
б
б
в
г
б
а
а
б
а
б
в
а
Домашнее задание
1. Задачи № 30, 31, 32 (учебник, стр. 245);
2. Желающие готовят к следующему уроку доклады по темам:
♦ Королев С. П.
♦ Терешкова В. А.
♦ Гагарин Ю. А.
♦ Циолковский К. Э.
♦ Первый человек на Луне.
Урок 25.
Реактивное движение. Ракеты.
Цели урока:
Познакомиться с особенностями и характеристиками реактивного движения, историей его развития.
Ход урока
I. Проверка домашнего задания
Поскольку тема реактивного движения основана на глубоком понимании закона сохранения импульса, то в начале урока следует повторить весь материал, изученный по данной теме. Можно провести краткий опрос:
- Всегда ли удобно пользоваться законами Ньютона для описания взаимодействия тел?
- Что такое импульс?
- Куда направлен вектор импульса?
- Сформулируйте закон сохранения импульса.
- Кто открыл закон сохранения импульса?
- Как проявляется закон сохранения импульса при столкновении тел? Решения домашних задач выписываются на доске и разбираются.
II. Новый материал
Начало изложения нового материала предполагает определение реактивного движения как одного из видов механического движения.
Движение, которое возникает как результат отделения от тела какой-либо части, либо как результат присоединения к телу другой части, называется реактивным движением.
На данном принципе работают реактивные самолеты и ракеты. Сила тяги обеспечивается реактивной тягой струи раскаленных газов.
Каракатицы, осьминоги при движении в воде также используют реактивный принцип перемещения. Набирая в себя воду, они, выталкивая ее, приобретают скорость, направленную в сторону, противоположную направлению выброса воды.
Простейшим примером реактивного движения является подъем воздушного шарика при выходе воздуха из него (учитель демонстрирует движение шарика).
В опыте с Г-образной трубкой учащиеся наблюдают, как трубка отклоняется в сторону, противоположную направлению струи.
После демонстрации опытов учитель задает вопросы:
- За счет чего возникает такое движение?
- Почему отклоняется трубка? Почему взлетает воздушный шарик?
- Почему движется ракета?
Согласно третьему закону Ньютона:
![]()
где ![]() - сила, с которой ракета действует на раскаленные газы, a
- сила, с которой ракета действует на раскаленные газы, a
![]() - сила,
с которой газы отталкивают от себя ракету.
- сила,
с которой газы отталкивают от себя ракету.
Модули этих сил равны: F1 = F2.
Именно сила ![]() и является реактивной
силой. Рассчитаем скорость, которую может приобрести ракета.
и является реактивной
силой. Рассчитаем скорость, которую может приобрести ракета.
Если импульс выброшенных газов равен mrvг, а импульс ракеты mpvp, то из закона сохранения импульса получаем:
![]()
откуда скорость ракеты:
![]()
Таким образом, скорость ракеты тем больше, чем больше скорость
истечения газов vr, и чем больше отношение ![]()
Ясно, что выведенная формула справедлива только для случая мгновенного сгорания топлива. Такого быть не может, так как мгновенное сгорание - это взрыв. На практике масса топлива уменьшается постепенно, поэтому для точного расчета используют более сложные формулы.
В заключение следует сказать, что современные технологии производства ракетоносителей не могут позволить превысить скорости в 8-12 км/с. Для третьей космической скорости (16,4 км/с) необходимо, чтобы масса топлива превосходила массу оболочки носителя почти в 55 раз, что на практике реализовать невозможно. Следовательно, нужно искать другие способы построения ракетоносителей. Возможно, и другие виды силовых двигателей.
Следует обратить внимание учеников на роль К. Э. Циолковского в развитии взглядов на теорию ракетостроения и освоения космического пространства.
III. Доклады
Заранее подготовленные ученики делают сообщения о жизни и научной деятельности С. П. Королева, К. Э. Циолковского, о Ю. А. Гагарине и В. А. Терешковой. Остальные учащиеся, по возможности, дополняют выступления.
IV. Вопросы для повторения
- Какое движение называют реактивным?
- Верно ли утверждение: для осуществления реактивного движения не требуется взаимодействия с окружающей средой?
- На каком законе основано реактивное движение?
- От чего зависит скорость ракеты?
- Когда и где был запущен первый искусственный спутник Земли?
Домашнее задание
1. Выучить § 21;
Урок 27.
Контрольная работа №2 по теме «Динамика. Закон сохранения импульса»
Цели урока:
Выявить знания учащихся по теме «Импульс. Закон сохранения импульса».
Ход урока
Вариант №1
1.С каким ускорением движется тело массой 3 кг, если на него действует сила 0,1 Н? Какова скорость тела в конце шестой секунды движения? Начальная скорость тела равна нулю.
2.Чему равно ускорение свободного падения на высоте, равной радиусу Земли?
3.Какова скорость тела, движущегося равномерно по окружности радиусом 3 м, если центростремительное ускорение равно 12 см/с2?
4.Железнодорожный вагон массой 20 т, скатываясь с сортировочной горки со скоростью 0,3 м/с, сталкивается с неподвижным вагоном массой 25 т. Какова скорость вагонов после автосцепки?
5.Как будет двигаться ракета, если на неё действует постоянная сила? постоянно убывающая сила?
----------------------------------------------------------------------------------------------------------------------------
Вариант №2
1.Два мальчика тянут веревку в разные стороны, прилагая силы 100 Н каждый. Веревка может выдержать, не разрываясь, груз весом 150 Н. Разорвется ли веревка?
2.На каком расстоянии от поверхности Земли сила притяжения космического корабля к ней станет в 100 раз меньше, чем на поверхности Земли?
3.Чем отличается изменения мгновенной скорости при прямолинейном и криволинейном движении?
4.Человек массой 60 кг движется навстречу тележке массой 30 кг и вскакивает на нее. Какова стала скорость тележки, если скорость человека в момент прыжка была равна 2 м/с, а скорость тележки составляла 1 м/с?
5.Почему шофер не может мгновенно остановить движущийся автомобиль?
-----------------------------------------------------------------------------------------------------------------------------
Вариант №3
1.Почему прыжковую яму наполняют песком и опилками, а не асфальтируют? Ответ поясните.
2.На тело массой 5 кг вдоль одной прямой действует две силы: F1 = 12 Н и F2 = 18 Н. Вычислите ускорение этого тела в случаях: угол между ними составляет 00; 1800.
3.Мальчик вращает камень на веревке, длина которой 1 м. Определите его центростремительное ускорение, если линейная скорость камня в верхней точке траектории составляет18 км/ч.
4.Снаряд массой 20 кг, движущийся в горизонтальном направлении со скоростью 0,5 км/с, попадает в платформу с песком массой 10 т и застревает в песке. Чему равна скорость платформы после столкновения?
5.Вычислите первую космическую скорость для Луны, если её масса составляет 7•1019 т, а средний радиус равен 1730 км.
-----------------------------------------------------------------------------------------------------------------------------
Вариант №4
1.Что притягивает к себе с большей силой: Земля - Луну или Луна - Землю?
2.Скорость материальной точки изменяется по закону vx =4 + 2t под действием силы 6 Н. Какова масса точки?
3.Из неподвижной лодки массой 255 кг (вместе с грузом) бросают груз в 5 кг с горизонтальной скоростью 10 м/с относительно Земли. Какую скорость при этом получила лодка?
4.Барон Мюнхгаузен, привязав конец веревки к Луне, спускался по ней на Землю. В чем главная физическая несуразность такого передвижения?
5.На какой высоте над поверхностью Земли ускорение свободного падения в 16 раз меньше, чем на земной поверхности? Радиус Земли 6400 км.
------------------------------------------------------------------------------------------------------------------------------
Вариант №5
1.Почему большинство спутников планет и астероидов не имеют собственной атмосферы?
2.Автомобиль массой 2 т, двигавшийся со скоростью 36 км/ч, остановился, пройдя после начала торможения путь 25 м. Определите величину тормозящей силы.
3.Почему автомобилю трудно тронуться с места на обледенелой дороге?
4.При постоянной скорости 900 км/ч самолет описывает «мертвую петлю». При каком радиусе петли его центростремительное ускорение не превысит 5g?
5.Человек бежит навстречу тележке. Скорость человека 2 м/с, скорость тележки 1 м/с. Человек вскакивает на тележку и остается на ней. Какой будет скорость тележки после этого, если масса человека в 2 раза больше массы тележки?
------------------------------------------------------------------------------------------------------------------------------
Вариант №6
1.При каких условиях движение тела по окружности является равномерным?
2.Под действием силы 150 Н тело движется так, что его координата в направлении действия силы изменяется по закону х = 100 + 5t + 5t2. Какова масса тела?
3.Вычислите первую космическую скорость на высоте 3R от поверхности Земли. Средний радиус Земли принять за 6400 км.
4.Почему, вытряхивая пыль из одежды, мы уверены, что таким образом часть пыли можно удалить?
5.Масса стрелка с лодкой - 100 кг, масса заряда - 20 г, а его скорость - 500 м/с. Какую скорость имела лодка до выстрела, если она остановилась после пятого выстрела?
------------------------------------------------------------------------------------------------------------------------------
Вариант №7
1.Как космонавту, находящемуся в открытом космосе, вернуться обратно на космический корабль без посторонней помощи?
2.Два одинаковых шарика массами 2 кг движутся навстречу друг другу. Скорость одного шарика 3 м/с, другого 7 м/с. Найдите величину суммарного импульса двух шариков.
3.Птица в клетке-ящике сидит на дне. Ящик с ней уравновешен на весах. Нарушится ли равновесие весов, если птица взлетит?
4.Что произойдет с силой взаимодействия двух тел, если массу одного из них и расстояние между ними увеличить в 2 раза?
5.Сила F сообщает телу массой m1 ускорение 2 м/с2, а телу массой m2 ускорение 3 м/с2. Какое ускорение под действием той же силы получат оба тела, если их соединить вместе?
----------------------------------------------------------------------------------------------------------------------------
Вариант №8
1.Чем объясняется наличие и периодичность морских приливов и отливов на Земле?
2.На тело действуют две силы под углом 900 друг к другу: F1 = 3 Н и F2 = 4 Н. Какова масса тела, если его ускорение составляет 2,5 м/с2? Решение сопроводите рисунком.
3.Почему во время ледохода на поворотах реки образуются заторы?
4.На тележку массой 100 кг, движущегося равномерно по гладкой горизонтальной поверхности со скоростью 3 м/с, вертикально падает груз массой50 кг. С какой скоростью будет двигаться тележка, если груз не соскальзывает с неё?
5.Сила тяготения между двумя одинаковыми шарами равна 0,01 Н. Каковы массы шаров, если расстояние между их центрами равно 1 м?
------------------------------------------------------------------------------------------------------------------------------
Вариант №9
1.Тело движется по: а) прямолинейной траектории с увеличивающейся по модулю скоростью; б) по прямолинейной траектории с уменьшающейся по модулю скоростью; в) по окружности с постоянной по модулю скоростью. Как направлена в каждом случае сумма всех сил, действующих на тело? Ответ обоснуйте.
2.На каком расстоянии от поверхности Земли сила тяжести, действующая на тело, уменьшается в 4 раза? (Радиус Земли принять равным 6400 км.)
3.Почему тело, брошенное с большой высоты, при достижении определенной скорости начинает двигаться равномерно?
4.С каким ускорением движется тело под действием силы 6 Н, если под действием силы 18 Н оно приобретает ускорение 2,1 м/с2?
5.Железнодорожный вагон массой 20 т, скатываясь с сортировочной горки со скоростью 0,3 м/с, сталкивается с неподвижным вагоном массой 25 т. Какова скорость вагонов после автосцепки?
------------------------------------------------------------------------------------------------------------------------------
Вариант №10
1.Может ли человек, стоящий на идеально гладкой горизонтальной (ледяной) площадке, сдвинуться с места, не упираясь острыми предметами в лед?
2.Вычислите первую космическую скорость для Марса, если радиус планеты равен 3380 км, а ускорение свободного падения составляет 3,86 м/с.
3.Вагон массой 15 т, движущийся со скоростью 3 м/с, сталкивается с платформой, масса которой 10 т, движущейся во встречном направлении со скоростью 2 м/с. При ударе вагон сцепляется с платформой. Какова скорость их совместного движения после удара?
4.Как будет двигаться ракета, если на неё действует: а) постоянная сила; б) постоянно убывающая сила?
5.Хоккейная шайба массой 250 г после удара клюшкой, длящегося 0,02 с скользит по льду со скоростью 30 м/с. Определить силу удар
Урок 28.
Колебательные движения. Величины, характеризующие колебательное движение
Цель урока:
Сформировать у учащихся представления о колебательном движении; изучить свойства и основные характеристики периодических (колебательных) движений. Ввести понятия амплитуды, периода и частоты колебаний; сформировать представление о гармонических колебаниях.
Ход урока
I. Анализ контрольной работы
II. Новый материал
Своеобразные движения, которые называются колебательными или просто колебаниями, всем хорошо известны. Они широко распространены в окружающем нас мире. Колеблются ветки деревьев во время ветра, качели и т. д.
На рис. 46 представлены нитяной и пружинный маятники.
Математическим маятником называется подвешенный к тонкой нити груз, размеры которого много меньше длины нити, а его масса много больше массы нити.
Итак, условия возникновения механических колебаний:
♦ Наличие положения устойчивого равновесия, при котором равнодействующая сила равна нулю.
♦ Хотя бы одна сила должна зависеть от координаты (например, Fупр = -kх).
♦ Наличие в колеблющемся теле избыточной энергии. (Вначале мы совершаем работу по сжатию пружины, сообщив ей некоторый запас энергии. За счет этой энергии и происходят колебания.)
♦ Если вывести тело из положения равновесия, то равнодействующая уже не будет равна нулю.
♦ Силы трения в системе достаточно малы.
Каждое движение характеризуется своими величинами.
- Какими величинами характеризуется равномерное прямолинейное движение? (Постоянной скоростью, координатой. Существует уравнение зависимости координаты от времени х = х0 +vxt.)
- Какими величинами характеризуется прямолинейное движение? (Постоянным ускорением, координатой.)
- Какими же величинами характеризуется колебательное движение?
Период колебаний
На прошлом уроке уже отмечалось, что колебательное движение - периодическое. Период Т - время одного полного колебания:
![]()
где t - все время движения, N - количество колебаний.
В СИ период колебаний выражается в секундах: [Т] = с.
Частота колебаний
Частота v - число полных колебаний за единицу времени:
![]()
где N - количество колебаний, t - время движения.
В СИ частота выражается в герцах: [v] = с-1 = Гц.
Колебательное движение характеризуются также циклической частотой:
![]()
Амплитуда колебания
Амплитуда х (или А) - наибольшее смещение от положения равновесия, измеряется в метрах (м). Можно измерять в единицах плоского угла (для математического маятника).
Графическое представление колебательного движения Так как в процессе колебаний положение тела меняется, то очень удобно изменение смещения тела от положения равновесия во времени представлять графически. Подготовив установку, предложенную в учебнике на стр. 97, учитель демонстрирует вид траектории движения тела. График зависимости смещения х от времени изображен на рис. 47. График показывает, что на каждом периоде колебаний Т амплитуда колебаний убывает. Это связано с наличием трения в системе. Если трение очень мало, то амплитуда убывает очень медленно, и колебания долго не затухают.
Полученная кривая называется синусоидой. (Несмотря на то, что такой термин используется в литературе, кривая, изображенная на рис. 47, не является истинной синусоидой - это более сложная функция. К сожалению, в 9 классе у ребят нет достаточных математических знаний, чтобы описать эту функцию. Истинная же синусоида показана на рис. 48.)
Периодические изменения во времени физической величины происходящие по закону синуса или косинуса, называются гармоническими колебаниями.
Закон изменения смещения х от времени t имеет вид:
![]()
Следует обратить внимание учеников, что по графику очень удобно определять все характеристики колебательного движения, а именно, период (T), амплитуду (А) и частоту (v).
Например, по графику колебаний, изображенному на рис. 48, определяем:
А = 0,1 м,
T = 0,8 с,
v = 1 /T = 1,25 Гц.
Для данного графика: 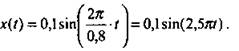
Далее можно предложить учащимся самостоятельно определить по заданному графику параметры движения тела.
Параметры колебательных систем
Чему же равны период и частота колебаний математического маятника, пружинного маятника?
а) Для пружинного маятника:
![]()
где m - масса груза, k - жесткость пружины.
Тогда частота колебаний:
![]()
б) Для математического маятника:
![]()
где l - длина нити, g - ускорение свободного падения
Частота колебаний:
![]()
Необходимо отметить отличие гармонических колебаний от негармонических. Период гармонических колебаний не зависит от способа выведения системы из положения равновесия (например, от амплитуды колебаний). В этом можно будет легко убедиться на следующем уроке в ходе лабораторной работы.
III. Закрепление .Решение задач
Задача 1
Маятник совершил 20 колебаний за 1 мин. 20 с. Найти период и частоту колебаний. (Ответ: T = 4 с; v = 0,25 Гц.)
Задача 2
Амплитуда незатухающих колебаний точки струны 2 мм, частота колебаний 1 кГц. Какой путь пройдет точка струны за 0,4 с? Какое перемещение совершит эта точка за один период колебаний? (Ответ: l = 3,2 м; S = 0.)
Задача 3
Координата колеблющегося тела изменяется по закону: х = 5cosπt. Чему равны амплитуда, период и частота колебаний, если в формуле все величины выражены в единицах СИ? (Ответ: А = 5 м; Т = 2 с; v = 0,5 Гц.)
Задача 4
Математический маятник длиной 2,45 м совершил 100 колебаний за 314 с. Определить ускорение свободного падения для данной местности. (Ответ: g = 9,8 м/с2.)
Задача 5
Какова длина математического маятника, совершающего гармонические колебания с частотой 0,5 Гц на поверхности Луны? Ускорение свободного падения на поверхности Луны 1,6 м/с2. (Ответ: l = 0,16 м.)
Задача 6
Груз массой 0,4 кг, подвешенный к невесомой пружине, совершает 30 колебаний в минуту. Чему равна жесткость пружины? (Ответ: k = 4 Н/м.)
III. Подведение итога.
- Какое движение называют колебательным?
- Что называют колебанием тела?
- Что называют амплитудой колебания? Периодом? Смещением?
- Что такое маятник? Какой маятник называют математическим?
- Какой маятник называют пружинным?
- Какие из перечисленных ниже движений являются механическими колебаниями: а) движение качелей; б) движение мяча, падающего на землю; в) движение звучащей струны гитары?
Домашнее задание
-
Выучить § 23;24
Урок 29.
Гармонические колебания.
Цель урока: сформировать у учащихся представление о гармонических колебаниях, как о гармонических изменениях координаты и других физических величин; ввести понятие амплитуды, периода, частоты, циклической частоты; получить формулу для вычисления периода свободных колебаний.
Ход урока
Проверка домашнего задания методом индивидуального опроса
1. Пояснить, используя чертеж, какие силы заставляют колебаться математический маятник.
2. Получить уравнение движение для пружинного маятника. у доски)
3. Получить уравнение движения математического маятника. (у доски)
Изучение нового материала
1. Изучив зависимость ускорения от координаты колеблющегося тела, найдем зависимость координаты от времени.
2. Ускорение - вторая производная координаты по времени.
а = - k x/m; x"= - k x/m; где х"- вторая производная координаты по времени.
Если колебания свободные, то координата х со временем изменяется так, что вторая производная координаты по времени прямо пропорциональна самой координате и противоположна ей по знаку.
3. Гармонические колебания
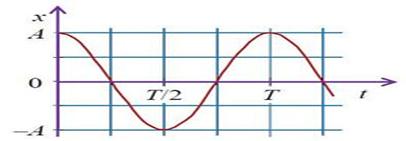
Координата х меняется со временем периодически. Нам известны две периодические функции: синус и косинус
Косинус при возрастании аргумента от нуля меняется медленно, приближаясь к нулю его изменения, происходят все быстрее.
Пружинный маятник, выведенный из положения равновесия, ведет себя точно так же. Синус и косинус обладают свойством, что вторая производная этих функций пропорциональна самим функциям, взятым с противоположным знаком.
На основании этого можно утверждать, что координата тела, совершающего свободные колебания, изменяется со временем по закону косинуса или синуса.
Периодические изменения физической величины в зависимости от времени, происходящие по закону синуса или косинуса, называются гармоническими колебаниями.
4. Амплитуда колебаний
Модуль наибольшего смещения тела от положения равновесия называют амплитудой гармонических колебаний.
Амплитуда - характеристика колебательного движения; она показывает как смещено тело от положения равновесия.
5. Решение уравнения движения, описывающего свободные
колебания. Запишем решение уравнения; х"= - k x/m; - X= xm QUOTE
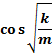
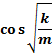 ·t;
Первая производная будет иметь вид: Xʹ= - QUOTE
·t;
Первая производная будет иметь вид: Xʹ= - QUOTE ![]()
![]() xm QUOTE
xm QUOTE
![]()
![]() ·t;
·t;
вторая производная будет равна: X"= - QUOTE ![]()
![]() xm QUOTE
xm QUOTE
![]()
![]() ·t = -
k x/m; то есть мы, получили первоначальное уравнение. Решением
этого уравнения будет также и функция; QUOTE
·t = -
k x/m; то есть мы, получили первоначальное уравнение. Решением
этого уравнения будет также и функция; QUOTE![]()
![]() ·t
·t
Из опытов получили
а= - k x/m a= - g x/L
![]()
![]()
![]()
![]() для
пружинного для математического маятника маятника
для
пружинного для математического маятника маятника
![]() ОБОЗНАЧИМ
ОБОЗНАЧИМ
![]()
![]()
![]() k/m ω02
g/L
k/m ω02
g/L
Имеем уравнения движения
а= - ω02x Подчиняются одной закономерности a= - ω02x
![]()
![]() a ~x x~x" x
"= - ω02x - решением этого дифференциального уравнения
a ~x x~x" x
"= - ω02x - решением этого дифференциального уравнения
является: x = xm QUOTE ![]()
![]() . График
зависимости координаты от времени представляет собой косинусоиду.
Гармонические колебания происходят по этому закону.
. График
зависимости координаты от времени представляет собой косинусоиду.
Гармонические колебания происходят по этому закону.
6. Период и частота гармонических колебанийПериод - время одного колебания.
Т=t/n; T= 1/γ; T=2π/ω0
Измеряется в 1с.
Частота - это число колебаний в единицу времени.
γ= 1/Т; γ= ω0/2π
Измеряется в 1/с; 1Гц
Циклическая (круговая) частота - число колебаний за 2π секунд.
ω0 Т= 2π; ω0=2π/Т = 2πγ
Закрепление изученного материала
Задача. Груз колеблющийся на пружине, за 8 с совершил 32 колебания. Найти частоту и период колебаний.
Решение. Т=t/n; γ = 1/T; T= 8/32 = 0,25 c; γ= 1/0,25 = 4 Гц
Подведем итоги урока
Домашнее задание: § 25
Урок 30.
Лабораторная работа №3 «Исследование зависимости периода и частоты свободных колебаний нитяного маятника от его длины»
Цель урока:
Проверить на практике справедливость теоретических соотношений по периоду колебаний нитяного маятника.
Оборудование: Шарик на нити, штатив с муфтой и кольцом, измерительная лента, часы (или секундомер).
Ход урока
Данная лабораторная работа позволяет экспериментально
подтвердить справедливость соотношения: ![]()
Перед выполнением работы нужно пояснить, что далеко не каждый нитяной маятник совершает колебания с периодом, определяемым данной формулой. И это нужно будет проверить в работе.
Очень важно, чтобы ученики выбрали длину подвеса нити в пределах 1-2 м. Это позволит получить значения Т с наивысшей точностью. При этом угол отклонения нити от вертикали не должен превышать 5-7°.
Указания к работе
1. Установите на краю стола штатив. К кольцу штатива подвесьте шарик на длинной нити (так, чтобы он находился на расстоянии 3-5 см от пола).
2. Измерьте длину нити I.
3. Отклоните шарик на 4-5 см от положения равновесия и отпустите.
4. Измерьте время t, за которое маятник сделает n = 30 полных колебаний.
5. Вычислите период и частоту колебаний.
6. Повторите опыт, уменьшив длину нити в 4 раза.
7. Результаты измерений и вычислений запишите в таблицу:
8. Сделайте вывод о зависимости периода и частоты колебаний маятника от длины нити.
Урок 31.
Затухающие колебания. Вынужденные колебания. Резонанс .
Цели урока:
Изучить возможные превращения энергии в колебательных системах. Подтвердить справедливость закона сохранения механической энергии в колебательных системах.
Ход урока
I. Проверка домашнего задания, повторение
- Что называется амплитудой, периодом колебания, частотой колебания? Какой буквой обозначается и в каких единицах измеряется каждая из этих величин?
- Что такое полное колебание?
- Какая математическая зависимость существует между периодом и частотой колебания?
- Как найти период математического маятника?
- От чего зависит период пружинного маятника?
- Как направлены по отношению друг к другу скорости двух маятников в любой момент времени, если эти маятники колеблются в противоположных фазах; в одинаковых фазах?
- Какие колебания называются гармоническими?
- Как меняются действующая на тело сила, его ускорение и скорость при совершении им гармонических колебаний?
II. Письменная проверочная работа
Вариант I
1. Какое из перечисленных ниже движений является механическим колебанием? 1) движение качелей; 2) движение мяча, падающего на землю.
а) только 1;
б) только 2;
в) 1 и 2;
г) ни 1, ни 2.
2. Какие из перечисленных ниже колебаний являются свободными? 1) колебания груза, подвешенного к пружине, после однократного его отклонения от положения равновесия; 2) колебания диффузного громкоговорителя во время работы приемника.
а) только 1;
б) только 2;
в) 1 и 2;
г) ни 1, ни 2.
3. За 4 с маятник совершает 8 колебаний. Чему равен период колебаний?
а) 8 с;
б) 4 с;
в) 2 с;
г) 0,5 с;
д) 32 с.
4. По условию задачи 3 определите частоту колебаний,
а) 8 Гц;
б) 4 Гц;
в) 2 Гц;
г) 0,5 Гц;
д) среди ответов а) - г) нет правильного.
5. На рис. 49 представлена зависимость координаты колеблющегося тела от времени. Какова амплитуда колебаний?
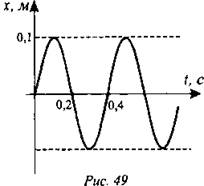
а) 0,2 м;
б) 0,1 м',
в) 1 м;
д) 0,4 м;
г) 0,5 м;
е) 0 м.
6. По рис. 49 определите, чему равен период колебаний?
a) 1 с;
б) 0,2 с;
в) 0,4 с;
г) 0,4 Гц;
д) 0,2 Гц;
е) 1 Гц.
7. По рис. 49 определите частоту колебаний.
а) 1 с;
б) 2 с;
в) 4 с;
г) 0,5 Гц;
д) 0,25 Гц;
е) 1 Гц.
II вариант
1. Какое из перечисленных ниже движений является механическим колебанием? 1) движение звучащей струны гитары; 2) движение спортсмена, совершающего прыжок в длину.
а) ни 1, ни 2;
б) 1 и 2;
в) только 1;
г) только 2.
2. Какие из перечисленных ниже колебаний являются вынужденными? 1) колебания груза на нити, один раз отведенного от положения равновесия и отпущенного; 2) колебания качелей, раскачиваемых человеком, стоящим на земле.
а) 1 и 2;
б) только 1;
в) только 2;
г) ни 1, ни 2.
3. За 3 с маятник совершает 6 колебаний. Чему равен период колебаний?
а) 6 с;
б) 3 с;
в) 2 с;
г) 0,5 с;
д) 18 с.
4. По условию задачи 3 определите частоту колебаний.
а) 0,5 Гц;
б) 2 Гц;
в) 3 Гц;
г) 6 Гц;
д) 1/16 Гц.
5. На рис. 50 представлена зависимость координаты колеблющегося тела от времени. Какова амплитуда колебаний?
а) -3 м;
б) 0;
в) 2 м;
г) 3 м;
д) 4;
е) 6 м.
6. По рис. 50 определите, чему равен период колебаний?
а) 2 с;
б) 4 с;
в) 8 с;
г) 0,5 Гц;
д) 0,25 Гц;
е) 1/8 Гц.
7. По рис. 50 определите частоту колебаний.
а) 2 с;
б) 4 с;
в) 8 с;
г) 0,5 Гц;
д) 0,25 Гц;
е) 1/8 Гц.
II. Новый материал
Рассмотрение нового материала удобно начать с показа колебаний грузов, закрепленных на нитях. Для наглядности удобно взять нити равной длины, а грузы - разной формы. Например, шарик и тонкую пластинку.
Легко заметить, что колебания во второй системе будут затухать быстрее, чем в первой (рис. 51).
Видно, что полная механическая энергия быстрее убывает во второй системе. Почему?
Ясно, что любая колебательная система будет совершать колебания до тех пор, пока обладает энергией. Отводя маятник от положения равновесия, мы сообщаем системе начальную энергию (рис. 52). Она равна потенциальной энергии тела: Ер = mgh.
Отпустив маятник, мы видим, что скорость тела возрастает, а значит, возрастает и его кинетическая энергия. Из закона сохранения механической энергии уменьшение Ер приводит к эквивалентному увеличению Ек. Для любой точки траектории, если в системе нет сил трения, справедливо: Е1 = Е2, т. е.:
![]()
Если тело находится в крайних положениях, система обладает полной энергией Е, определяемой только потенциальной энергией. А в положении равновесия полная энергия равна максимальной кинетической энергии груза:
![]()
Важно понять, что составляющие полной энергии Ек и Ер не просто изменяются во времени, а изменяются периодически с заданным периодом колебаний в системе. Период изменения Еки Ер в 2 раза меньше периода колебаний Т.
Обычно реальные системы обладают собственным трением, и присутствует сила сопротивления среды.
Поэтому колебания в таких системах являются затухающими: полная механическая энергия начинает уменьшаться, т. к. уходит на преодоление сил трения. Следовательно, амплитуда колебаний уменьшается, и, когда работа силы трения становится равна по модулю исходной полной энергии в системе, колебания прекращаются.
Но на колебательную систему может действовать периодическая внешняя сила. Такая сила называется вынуждающей силой.
Тряска автомобиля, движущегося по неровной дороге, движение качелей, которые кто-то периодически подталкивает - все это вынужденные колебания.
Свободные колебания с течением времени затухают. Поэтому на практике чаще используются не свободные колебания, а вынужденные. Наиболее широко они применяются в различных вибрационных машинах.
III. Закрепление изученного
- Опишите процесс превращения энергии при гармоническом колебательном движении на примере математического маятника.
- Почему свободные колебания маятника затухают? При каких условиях колебания могут стать незатухающими?
- Начертите график затухающего колебания.
- Чем определяется частота свободных колебаний? Почему ее называют собственной частотой колебательной системы?
- В каких машинах применяются вынужденные колебания?
IV. Решение задач
1. Маятник совершил 180 колебаний за 72 с. Определите период и частоту колебаний. (Ответ: 0,4 с; 2,5 Гц.)
2. Шарик, подвешенный на длинной нити, отклонили от положения равновесия так, что его высота над землей увеличилась на 5 см. С какой скоростью пройдет этот шарик положение равновесие в процессе свободных колебаний? (Ответ: 1 м/с.)
3. Вычислите частоту свободных колебаний маятника, у которого нить имеет длину 1 м. Сколько времени будут длиться 10 колебаний этого маятника? (Ответ: 0,5 Гц.)
4. В Исаакиевском соборе в Петербурге висел маятник с длиной подвеса 98 м. Чему равен период его колебаний? Сколько колебаний он совершает за 1 минуту? (Ответ: 20 с; 3 колебаний.)
Домашнее задание
1. § 26,27
Урок 32.
Распространение колебаний в упругих средах. Поперечные и продольные волны.
Цели урока:
Познакомить учащихся с условиями возникновения волн и их видами (поперечная волна, продольная волна)
Ход урока
I. Проверка домашнего задания, повторение
- С какой целью и как проводились опыты с двумя маятниками, изображенными на рис. 63 учебника?
- В чем заключается явление, называемое резонансом?
- Какой из маятников, изображенных на рис. 64 учебника, колеблется в резонансе с маятником 3? По каким признакам Вы это определили?
- К каким колебаниям - свободным или вынужденным - применимо понятие резонанса?
- Приведите примеры, показывающие, что в одних случаях резонанс может быть полезным явлением, а в других - вредным.
II. Новый материал
Начать урок можно с вопроса классу:
- Что такое волна, как вы понимаете? (Ответы учеников.)
Колебания, которые перемещаются в пространстве с течением времени,
называются волной.
Самым простым видом колебаний являются волны, возникающие на поверхности жидкости, и расходящиеся из места возмущения в виде концентрических окружностей.
Проецируя на экран расходящиеся волны в демонстрационной ванне (рис. 54), учитель подчеркивает, что их перемещения по всем направлениям равноправны.
Такое представление волны как чередование горбов и впадин достаточно наглядно: можно легко определить, как быстро меняется положение гребня, а, значит, оценить скорость волны.
Возникновение механической волны легко продемонстрировать на примере колебаний в гибком шнуре. Один конец шнура жестко укрепляют в точке А, а свободный конец хлыстовым движением перемещают в вертикальной плоскости. По шнуру начинает бежать упругая волна к точке А. В данном случае источником возмущения упругой среды была рука.
Важно подчеркнуть, что волна возникает лишь тогда, когда вместе со внешним возмущением появляются силы в среде, противодействующие ему. Обычно это силы упругости.
Механические волны возникают и перемещаются лишь в упругих средах. Такие среды достаточно плотные и соударение частиц в них напоминает упругое соударение шаров. Именно это позволяет частицам в волне передавать избыток энергии соседним частицам. При этом частица, передав часть энергии, возвращается в исходное положение. Этот процесс продолжается дальше. Таким образом, вещество в волне не перемещается. Частицы среды совершают колебания около своих положений равновесия.
Чем более разрежена среда, тем быстрее затухает волна в ней, и тем меньше ее скорость.
В зависимости от того, в каком направлении частицы совершают колебания по отношению к направлению перемещения волны, различают продольные и поперечные волны.
В продольной волне частицы совершают колебания в направлениях, совпадающих с перемещением волны. Такие волны возникают в результате сжатия-растяжения. Следовательно, они могут возникнуть и в газах, и в твердых телах, и в жидкостях.
В поперечной волне частицы совершают колебания в плоскостях, перпендикулярных направлению перемещения волны. Такие волны - результат деформации сдвига. Значит, эти волны могут возникать лишь в твердых телах, ибо в газах и жидкостях такой вид деформации невозможен.
При распространении волны происходит передача движения от одного участка тела к другому. С передачей движения волной связана передача энергии без переноса вещества. Энергия поступает от источника. При распространении волны происходит постепенное уменьшение амплитуды колебаний из-за превращения части механической энергии во внутреннюю.
III. Упражнения и вопросы для повторения
- Что называется волной?
- Какие волны называются поперечными?
- Какие волны называются продольными?
- В чем заключается необходимое условие возникновения волны?
- В каких средах распространяются продольные и поперечные волны?
- Происходит ли в бегущей волне перенос вещества?
Домашнее задание
1. §28 читать
Урок 33.
Длина волны скорость распространения волн.
Цели урока:
Ввести понятия длины волны, скорости распространения волны, частоты; учить решать задачи по данной теме.
Ход урока
I. Проверка домашнего задания, повторение
- Что называется волнами?
- В чем заключается основное общее свойство бегущих волн любой природы?
- Что такое упругие волны?
- Какие волны называются продольными, поперечными?
- В каких средах они распространяются?
II. Новый материал
Переходя к изложению нового материала, следует заметить, что любой физический процесс всегда описывается рядом характеристик, значения которых позволяют более глубоко понимать содержание процесса. Волновые явления в упругих средах также имеют определенные характеристики.
К ним можно отнести скорость волны (v), длину волны (λ), амплитуду колебаний в волне (А), период и частоту колебаний (Т, v).
Скорость механических волн, в зависимости от вида волны и упругих свойств сред, может меняться от сотен метров в секунду до 10-12 нм/с.
Под длиной волны λ понимают то расстояние, которое проходит волна за время, равное периоду колебаний.
Совершенно очевидно, что для конкретной среды длина волны должна быть конкретной величиной:
![]()
Представим графически волну как колебания, которые
перемещаются в пространстве с течением времени (рис. 55). Длина
волны: λ = 1000 м. Период колебаний: Т = 0,4 с. Скорость волны:
![]()
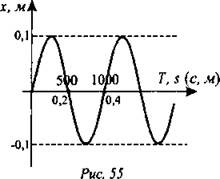
Следует заметить, что частота колебаний в волне всегда совпадает с частотой колебаний источника волны.
При этом упругие свойства среды не сказываются на частоте колебания частиц.
Лишь при переходе волны из одной среды в другую происходит изменение скорости и длины волны, а частота колебаний частиц остается по-прежнему постоянной.
- При какой частоте колебаний в вашей экспериментальной работе длина волны была больше? (При меньшей частоте.)
III. Упражнения и вопросы для повторения
- Что называют периодом волны? Частотой, длиной волны?
- Напишите формулу, связывающую скорость распространения волны с длиной волны и частотой или периодом.
- Как понять, что колебания происходят в одинаковых фазах, противофазах, со сдвигом фаз?
IV. Решение задач
Задача 1
Расстояние между ближайшими гребнями волны в море 20 м. С какой скоростью распространяется волна, если период колебаний частиц в волне 10 с? (Ответ: v = 2 м/с.)
Задача 2
Рыболов заметил, что за 5 с поплавок совершил на волнах 10 колебаний, а расстояние между соседними гребнями волн 1 м. Какова скорость распространения волн? (Ответ: v = 2 м/с.)
Задача 3
Частота колебаний в волне 10000 Гц, а длина волны 2 мм. Определить скорость волны.
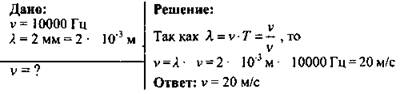
Задача 4
Длина волны равна 2 м, а скорость ее распространения 400 м/с. Определить, сколько полных колебаний совершает эта волна за 0,1 с.
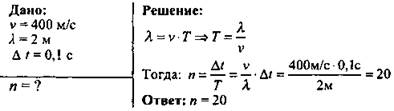
Задача 5
Мимо неподвижного наблюдателя, стоящего на берегу озера, за 6 с прошло 4 гребня волны. Расстояние между первым и третьим гребнями равно 12 м. Определить период колебания частиц волны, скорость распространения и длину волны. (Ответ: λ = 6 м; Т = 2 c; v = 3 м/с.)
Задача 6
Волна от катера, проходящего по озеру, дошла до берега через 1 мин., причем расстояние между соседними гребнями оказалось равным 1,5 м, а время между двумя последовательными ударами волн о берег - 2 с. Как далеко от берега проходил катер? (Ответ: l = 45 м.)
Домашнее задание
1. Выучить § 29
</