Построение касательной к окружности

ПРЕДМЕТ: ЧЕРЧЕНИЕ

Тема урока «Построение касательной к окружности»

Цель: Дать понятие о секущей и касательной, умение правильно строить касательную к окружности.

Задачи: Знать отличие секущей и касательной, уметь грамотно пользоваться чертежными инструментами при построении 3 видов касательных навыков в вычерчивании.

План урока:

1. Орг. момент - 1 мин.

2. Повторение. Работа у доски учащегося - 7 мин.

3. Новая тема. Записи терминологии.

4. Этапы вычерчивания касательной. Работа учителя у доски. Поэтапное изображение 3 видов (повтор учениками).

Контроль успешности работы и записи в тетрадь - 30 мин.

5. Определение по предложенным изображениям видов касательных - 5 мин. (закрепление).

6. Домашнее задание. Итог урока 2мин.

Ход урока:

1. Орг. момент.

2. Повторение: учащимся предлагается у доски и в тетрадях разделить окружность на 5 и 7 разных частей, построив правильные пяти и семиугольники.

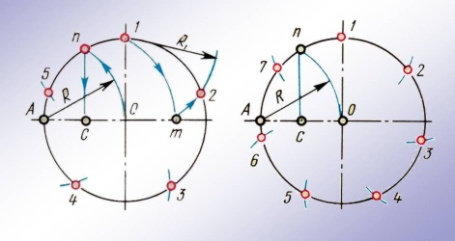
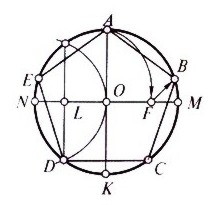
3. Изложение нового материала. Сначала выполняют чертеж - схему в тетрадях с доски.

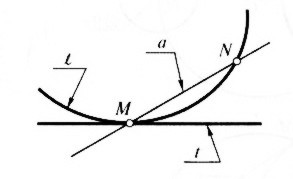
Прямую проходящую через 2 точки кривой е называют секущей. Единственная точка соприкосновения (М) к прямой t называется точкой касания, а прямая t - касательной к кривой е.

4. Рассмотрим пример. 1 построения касательной между точкой А и окружностью.

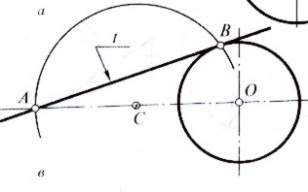Дано: т. А и окружность

Найти: касательную

Решение:

1. т. А соединяем с центром окружности О.

2. находим середину отрезка АО -т.С

3.из т. С проводим окружность, проходящую через т. А и т.О

4.Т. Пересечения окружностей - В точка КАСАНИЯ

5. прямая проходящая через т. А и - В - точка касания т. В - искомая касательная

Пример №2

Дано: 2 окружности

Найти: общую касательную.

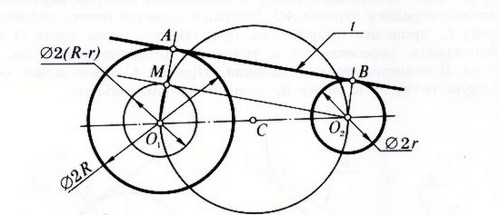
Решение:

1. вспомогательную окружность =R-r

2. от ц. О₁ до ц. О₂ - отрезок делим на 2 равные части и получаем т. С.

3. через т. С проводим окружность проходящую через т. О₁ и О₂, точка пересечения этой окружности со вспомогательной образует т. М.

4. соединяем М с О₂ из этих точек проводим  и получаем т. А и т. В - точки касания.

5. через точки А и В проводим касательную.

Пример №3

Дано: 2 окружности.

Найти: общую касательную, где точка касания от прямой соединяет центры по разные стороны.

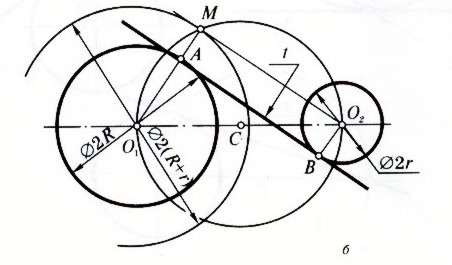
Решение:

1. Соединяем центры окружности R и r

2. находим центр между окружностями О₁,О₂ - т. С

3. из т. С проводим вспомогательную окружность проходящую через т. О₁ и О₂

4. из т. О₁ проводим R₅=R+r

5. Пересечение R_б со вспомогательной окружностью образует т. М

6. Соединяем т. М. с центром О₂

7. из т. М и О₂ опускаем  и получаем точки пересечения с данными окружностями А и В - являются точками касания.

8. прямая проходящая через т. А и т. В - искомая касательная

5. Закрепление видов касательных

А) между точкой и окружностью

Б) внешняя касательная двух окружностей

В) внутренняя касательная двух окружностей - определения по плакату.

6. Д/задание Параграф - 8, упр. №1, №2.