Статья на тему: Геодезические линии

Хаматнурова А.А.

БФ БашГУ, г. Бирск, РБ

Беляев П.Л., к.ф.-м.н., доцент

Геодезические линии поверхности «гиперболический параболоид»

Геодезические линии на поверхности второго порядка трансцендентны и были впервые определены Якоби в 1837 г. с помощью гиперэллиптических интегралов. [2] Геодезическая линия является кратчайшим путем перехода от одной точки пространства до другой. Рассмотрим задачу об отыскание данных линий на поверхности «Гиперболический параболоид» (рисунок 1).

Задача. Найти геодезические линии гиперболического параболоида заданного параметрическим уравнением [1].

Решение. 1) Пусть линия - искомая геодезическая. Ее задает система дифференциальных уравнений:

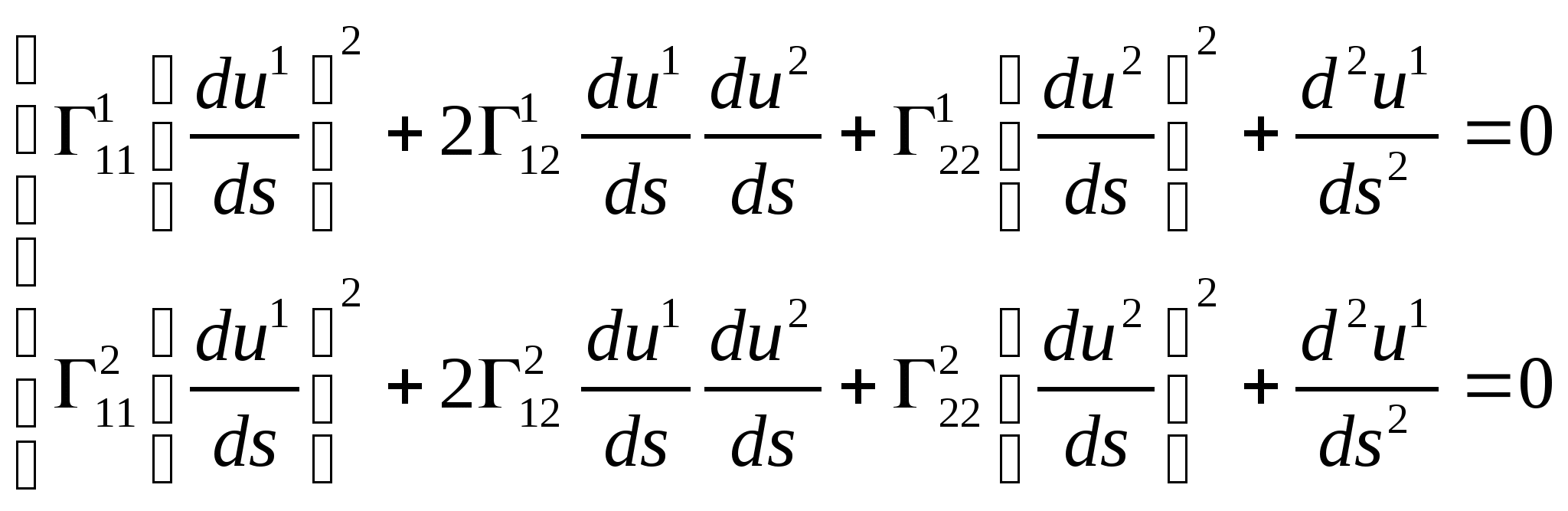(1)

2) Вычислим символы Кристоффеля:

,, ,..

3) Подставим в (1), получим следующие решения:

а) ;

б) ;

в) .

Умножим на и, выразив из второго уравнения , подставим в первое:

,

где - константы.

Заметим, что при получим . Это уравнение параболы.

Для построения поверхности «Гиперболический параболоид» был использован математический пакет MathCad. Он является простой в использовании и очень удобной программой для построения графиков.

Искомая поверхность представлена на рис. 1.

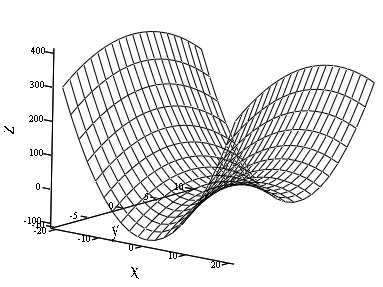
Рис.1 Гиперболический параболоид

Таким образом, в работе были найдены геодезические линии поверхности «Гиперболический параболоид», которая задана параметрическими уравнениями.

Литература

1. Александрова Е. В. Дифференциальная геометрия в задачах. Методические рекомендации. - Бирск, - 2003.-78 с.

2. Мищенко А. С., Фоменко А. Т. Курс дифференциальной геометрии и топологии. - М.: Издательство «Факториал Пресс», - 2013. - 448 с.

3. Сизый С. В. Лекции по дифференциальной геометрии. -М.: ФИЗМАТЛИТ, - 2013. - 376 с.