Конспект урока на тему: 'Возрастание и убывание функции' (11 класс)

Конспект урока по алгебре (11 класс).

Выполнила: Склярова София.

Тема урока: «Возрастание и убывание функции».

Цель:

• • образовательная: изучить достаточные условия возрастания и убывания функций, научить применять понятие производной для нахождению промежутков монотонности функции;

• развивающая: развитие навыков самоконтроля, внимательности; развитие мыслительной деятельности учащихся;

• воспитательная: воспитание точности, аккуратности, уважению к труду одноклассников, ответственности за результаты своего труда и труда одноклассника.

Тип урока: урок изучения нового материала.

Методы обучения: дедуктивно-репродуктивный, индуктивно-репродуктивный.

Оборудование: презентация, интерактивная доска.

Литература:

1. Алгебра и начала математического анализа: Учеб. для 11 кл. общеобразоват. учреждений: базовый и профил. уровни/ Ю.М.Колягин, М.В.Ткачёва, Н.Е.Фёдоровна, М.И.Шабунин; под ред. А.Б.Жижченко. − 3-е изд., - М.: Просвещение, 2011. − 336 с.

2. Репетиционные варианты Единый государственный экзамен 2015, Математика. 12 вариантов. Учебное пособие./ А.В.Семенов, И.Р.Высоцкий, И.В.Ященко; под ред. И.В.Ященко; Федеральный институт педагогических измерений. - М.: Интеллект-Центр, 2015.

План урока:

1. Организационный момент (1 мин.)

2. Актуализация опорных знаний (10 мин.)

3.Изучение нового материала (16 мин.)

4. Закрепление изученного материала (12 мин.)

5. Подведение итогов урока (5 мин.)

6. Домашнее задание (1 мин.)

Ход урока

1. Организационный момент.

Учитель приветствует учеников, проверяет отсутствующих, готовность помещения к уроку.

Учитель: запишите число, классная работа и название темы в тетрадь.

(запись в тетрадях)

Число

Классная работа

Возрастание и убывание функции.(Слайд 1)

2. Актуализация знаний.

Учитель: Что называется производной функции f(x) в точке x₀? (Слайд2)

Ученик: Производной функции f '(x) в точке x₀ называется предел разностного отношения при h→0, т.е. f '(x₀)=.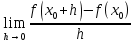

Учитель: Чему равны производные постоянной функции, линейной функции, степенной функции? (Слайд2)

Ученик: Производная постоянной функции с'=0.

Производная линейной функции (kx+b)'=k.

Производная степенной функции (х^р)'=р*х^р-1, pϵR, x>0.

Учитель: Сформулируйте правило дифференцирования суммы. (Слайд2)

Ученик: (f(x)+g(x))'=f '(x)+g '(x).

Учитель: Сформулируйте правило дифференцирования произведения. (Слайд2)

Ученик: (f(x)*g(x))'=f '(x)*g(x)+f(x)*g '(x).

Учитель: Сформулируйте правило дифференцирования частного. (Слайд2)

Ученик: .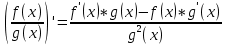

Учитель: Напишите производные элементарных функций. (Слайд 3)

(sin x)'; (cos x)'; (ln x)'; (e^x)'; (tg x)'; (ctg x)'; (ln|x|)'; (a^x)'; (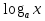)'; (x^p)'.

Ученик: (sin x)'= cos x

(cos x)'= -sin x

(ln x)'=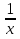, х>0.

Ученик: (e^x)'=е^х

(tg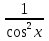 x)'= ,x≠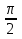+kπ, kϵz.

(ctg x)'=-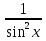 ,x≠kπ, kϵz.

Ученик: (ln|x|)'=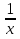, х≠0

(a^x)'=а^хln a, a>0, a≠1.

Ученик: (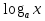)'= 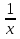,a>0, a≠1, x>0.

(x^p)'=px^p-1, pϵR, x>0.

3. Изучение нового материала.

Учитель: С помощью производной можно находить промежутки монотонности функции. Условимся термин «промежуток» использовать для обозначения таких числовых множеств, как отрезок [a;b], интервал (a;b), полуинтервалы [a;b) и (a;b].

При этом точки a и b называют граничными точками, а все остальные точки интервала (a;b)-внутренними точками промежутка.

Учитель: Функция f(x) называется возрастающей на некотором промежутке, если большему значению аргумента соответствует большее значение функции, т.е. для любых точек x₁ и x₂ из этого промежутка, таких, что x₂>x₁, выполняется неравенство f(x₂)>f(x₁). (Слайд 3)

Учитель: Если для любых точек х₁ и х₂ данного промежутка, таких, что х₂>x₁, выполняется неравенство f(x₂)<f(x₁), то функция f(x) называется убывающей на этом промежутке.

Промежутки возрастания и убывания функции называются промежутками монотонности этой функции.

Учитель: Пусть функция f(x) непрерывна на отрезке [a;b] и дифференцируема на интервале (a;b). Тогда если f'(x)>0 для всех xϵ(a;b), то функция f(x) возрастает на отрезке [a;b], а если f'(x)<0, то она убывает на этом отрезке. (Слайд 4)

Применяя определение возрастающей (убывающей) функции трудно найти промежутки монотонности, поэтому мы будем изучать признаки монотонности функции, использующие понятие производной.

Учитель: При доказательстве теорем о достаточных условиях возрастания или убывания функции используется следующая теорема, которая называется теоремой Лагранжа.

Учитель: Пусть функция f(x) непрерывна на отрезке [a;b] и дифференцируема на интервале (a;b). Тогда существует точка, такая cϵ(a;b), что f(b)-f(a)=f'(c)(b-a). (Слайд 5)

Запись в тетрадях:

f(b)-f(a)=f'(c)(b-a).(1)

Учитель: Эта теорема доказывается в курсе высшей математик. Поясним геометрический смысл формулы (1). Проведем прямую l (рис.56 из учебника) через точки A(a, f(a)) и B(b, f(b)) графика функции y=f(x) и назовем эту прямую секущей. Угловой коэффициент k секущей l равен

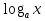
Равенство (1) можно записать в виде

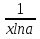
Из равенства (2) и (3) следует, что угловой коэффициент 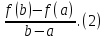касательной к графику функции y=f(x) в точке C с абсциссой c равен угловому коэффициенту k секущей l.

Таким образом, на интервале (a;b) найдется такая точка c, что касательная к графику функции y=f(x) в точке C(c; f(c)) параллельна секущей l.

Учитель: Давайте запишем алгоритм нахождения промежутков возрастания и убывания: (Слайд 6)

1. Находим производную функции.

2. Находим, при каком значении х, производная функции равна нулю.

3. Находим промежутки, на которые найденная точка разбивает ось Ох, и находим значение производной функции в какой - нибудь точке каждого из интервалов.

4. Находим промежутки возрастания и убывания функции.

Учитель: Давайте рассмотрим функцию f(x)=2х²+4х-4. (Слайд 6)

Сначала находим производную этой функции.

f '(x)= (2х²+4х-4)'=4x+4.

Затем производную f'(x) приравниваем к нулю и находим значение х.

f '(x)=0, т.е. 4х+4=0; х=-1.

После этого отмечаем значение х на числовой оси и выясняем какие знаки будут на интервалах.

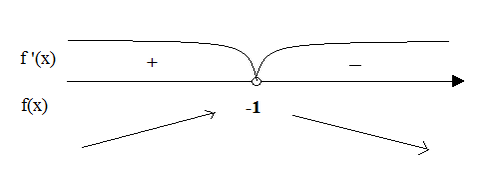
Делаем вывод: т.к. f '(x)>0 на интервале (-∞;-1), то функция f(x) - возрастает;

а на интервале (-1; +∞) функция f(x) -убывает, т.к. f '(x)<0.

Промежутки возрастания и убывания функции называются промежутками монотонности этой функции. (Слайд 4)

Учитель: При доказательстве теорем о достаточных условиях возрастания или убывания функции используется следующая теорема, которая называется теоремой Лагранжа.

Учитель: Прочитайте вслух первую теорему из учебника.

Ученик: Пусть функция f(x) непрерывна на отрезке [a;b] и дифференцируема на интервале (a;b). Тогда существует точка, такая cϵ(a;b), что f(b)-f(a)=f'(c)(b-a).

Запись в тетрадях:

f(b)-f(a)=f'(c)(b-a).

Учитель: Прочитайте нам вторую теорему.

Ученик: Пусть функция f(x) непрерывна на отрезке [a;b] и дифференцируема на интервале (a;b). Тогда если f'(x)>0 для всех xϵ(a;b), то функция f(x) возрастает на отрезке [a;b], а если f'(x)<0, то она убывает на этом отрезке. (Слайд 7)

4. Закрепление изученного материала.

Учитель: Ребята а теперь открываем №1 в учебнике на странице 101 и решаем под цифрами 1,3. Что нам нужно найти в данном задании? (Слайд 8)

Ученик : Нам нужно найти интервалы возрастания и убывания функции.

(Запись на доске и в тетрадях)

Учитель: Что является первым шагом алгоритма решения таких задач:

Ученик: Найдем производную функции

Учитель: Какого вида функция f(x)=5x²-3x-1, является ли она сложной?

Ученик: Функция сложная, представляет собой сумму нескольких функций, значит найдем производные каждого из слагаемых

f(x)=5x²-3x-1

f '(x)=(5x²-3x-1)'=(5x²)-(3x)-1=10x-3

Учитель: Каков следующий шаг решения?

Ученик: Найдем ,при каком значении х, производная функции равна нулю: f '(x)=0; 10x-3=0; x=0,3.

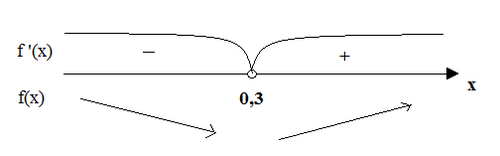
Ученик: Определяем промежутки возрастания и убывания функции.

Ответ: на интервале (-∞; 0,3) - функция f(x) - убывает, т.к. f '(x)<0;

на интервале (0,3; +∞) - функция возрастает, т.к. f '(x)>0.

Ученик: Найти интервалы возрастания и убывания функции.

(Запись на доске и в тетрадях)

Учитель: Что является первым шагом алгоритма решения таких задач:

Ученик: Найдем производную функции

Учитель: Какого вида функция f(x)=2х³+3х²-4, является ли она сложной?

Ученик: Функция сложная, представляет собой сумму нескольких функций, значит найдем производные каждого из слагаемых

f '(x)=( 2х³+3х²-4)'=( 2х³)'+(3х²)'-(4)' =6х²+6х

Учитель: Каков следующий шаг решения?

Ученик: Найдем, при каком значении х, производная функции равна нулю: f '(x)=0; 6х²+6х =0; 6х(х+1)=0; x₁=0, х₂=-1.

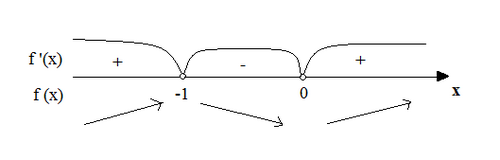
Ученик: Определяем промежутки возрастания и убывания функции.

Ответ: на интервалах (-∞; -1) и (0; +∞) - функция f(x) возрастает, т.к. f '(x)>0;

на интервале (-1;0) - функция убывает, т.к. f '(x)<0.

Учитель: Теперь в тетрадях решим подобное задание под №2 так же под цифрами 1,3.

f(x)=х²-3х+4

f(x)=х³-3х

Ученик: Найти интервалы возрастания и убывания функции.

(Запись в тетрадях).

Решение:

1. f(x)=х²-3х+4

f '(x)=(х²-3х+4)'=2х-3

f '(x)=0; 2х-3 =0; х=1,5.

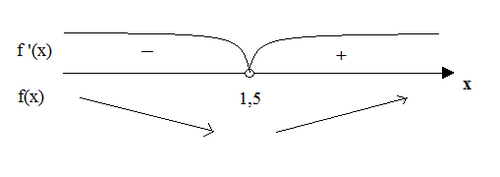
Ответ: на интервале (-∞; 1,5) - функция f(x) - убывает, т.к. f '(x)<0;

на интервале (1,5; +∞) - функция возрастает, т.к. f '(x)>0.

Ученик: Найти интервалы возрастания и убывания функции.

(Запись в тетрадях).

3) f(x)=х³-3х

f '(x)=( х³-3х)'=3х²-3

f '(x)=0; 3х²-3=0; x₁=-1; х₂=1.

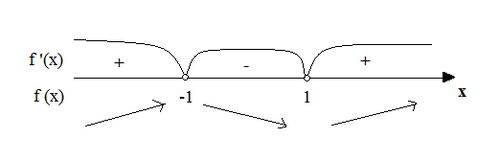
Ответ: на интервалах (-∞; -1) и (1; +∞) - функция f(x) - функция возрастает, т.к. f '(x)>0;

на интервале (-1; 1) - функция убывает, т.к. f '(x)<0.

5. Подведение итогов урока.

Учитель: Итак, урок подходит к концу, давайте подведем итоги. Назовите тему сегодняшнего урока.

Ученик: Возрастание и убывание функции.

Учитель: При каких значениях производной функция возрастает?

Ученик: Функция возрастает, когда производная больше нуля. f '(x)>0.

Учитель: При каких значениях производной функция убывает?

Ученик: Функция убывает, когда производная меньше нуля. f '(x)<0.

Учитель: При каких значениях производной функция постоянна?

Ученик: Функция постоянна, когда производная равна нулю. f '(x)=0.

6. Домашнее задание.

Учитель: Записываем домашнее задание: учебник Глава 3 §1 выучить теорему 1,2 и определения, № 1(2,4), №2(2,4). (Слайд 9)

Выставление оценок.

Урок окончен.