Открытый урок в 7 классе (в незнакомом классе) по теме 'Куб суммы и разности двух выражений'

Открытый урок в 7 классе ( в незнакомом классе)

ТЕМА: Куб суммы и разности двух выражений

Цели урока:

• Образовательные:

  • проверка усвоения формул «квадрат суммы и разности двух выражений» «разность квадратов», «сумма и разность кубов»;

  • вывод формул «куб суммы и разности двух выражений» умение применять их при преобразованиях выражений с целью упрощения.

• Развивающие:

  • развитие умения сравнивать, анализировать, обобщать, делать выводы, правильно формулировать и излагать мысли;

  • развитие интереса к предмету через содержание учебного материала, расширение кругозора.

• Воспитательные:

  • воспитание навыков самоконтроля и взаимоконтроля;

  • воспитание культуры общения, умения работать в парах, группе коллективе, взаимопомощи;

  • воспитание внимательности, таких качеств характера как настойчивость в достижении цели, умение не растеряться в проблемных ситуациях.

Тип урока: изучение нового материала

Формы организации познавательной деятельности: индивидуальная, парная, групповая

Средства: доска, компьютер, мультимидийный проектор, авторская презентация, ватманы, фломастеры

Ход урока

1.Оргмомент. Настрой на урок.

Здравствуйте, ребята! Раз уж мы стоим, давайте глубоко вздохнем, а теперь выдохнем, поймаем глазами друг друга, улыбнемся, поймаем тишину и тихо сядем.

Меня зовут Валентина Ивановна Похабова. Я представляю Большесырскую среднюю школу. И хочу попросить вас помочь мне провести сегодняшний урок.

Итак, начинаем. Ребята,

«У математиков существует свой

язык - это формулы»

Софья Васильевна Ковалевская

(Русский математик, механик, первая женщина - профессор в мире.)

- Я, уверена, вы догадались, о чем пойдет речь сегодня на уроке?

(О формулах сокращенного умножения)

Замечательно! Откройте тетради, запишите на полях число 26.02.15. и тему урока:

«Формулы сокращенного умножения»

- кстати, почему их так называют?

(потому что это отдельные случаи, когда умножение двух многочленов приводит к компактному, легко запоминающемуся результату) они позволяют заменить произведение многочленов готовым результатом.

2 . Актуализация опорных знаний.

В начале урока я предлагаю повторить ФСУ с помощью игры «Верю-не верю».

Возьмите сигнальные круги. Я буду предлагать утверждения, а вы сигналом отвечать.

Красный цвет означает - нет, не верю;

Желтый - сомневаюсь;

Зеленый - да, верю.

В тетрадях будете фиксировать свои результаты «плюсом» и «минусом».

Поставьте в тетради цифру 1, 2 и т.д.

Нет Да

Нет

Нет

Нет

С

Итак, верите ли вы, что равенство верное:

1. (a + b)² = a² + b² У кого горит красный цвет, поставьте «+», остальные «-«. Почему, Ваня, у тебя горит

2. (a - b)(a + b) = a² - b² Почему? зеленый? Прочитай формулу.

3. (a + b)(a² +2ab +b²) = a³ + b³ Почему? Кто скажет, в чем ошибка

4. (a - b)² = a² - 2ab - b² Почему? Вани? И т.д.

5. (a - b)(a² - ab - b²) = a³- b³ Почему?

6. (a - b)³ = a³ - 3ab + b³ У кого горит красный цвет, поставьте «+», остальные «-«.

- Поднимите руки, у кого 6 плюсов, 5 плюсов, 4,3?

- Поднимите руки , кто верно ответил на 6 задание? Почему это задание вызвало затруднение?

- Что нам предстоит узнать сегодня на уроке? Что такого нужно сделать, чтобы преодолеть эти трудности?

(Возможные варианты вопросов: Чему мы будем учиться сегодня на уроке? Что мы с вами знали и что предстоит узнать? Какую общую цель мы можем поставить сегодня на уроке ?)

Сформулируйте цели урока:

Цели: Вывести формулы возведения в куб суммы и разности двух выражений (a+b)³=…. (a-b)³=… и научиться их применять.

Или вывести формулы кубов суммы и разности двух выражений и научиться их применять.

3. Открытие новых знаний.

-Чтобы решить любую задачу, тем более трудную задачу, что нужно знать, на что опираться?

(теорию (на факты): определения, правила, те же самые формулы сокращенного умножения, свойства, алгоритмы...; на опыт, навык…)

- Верно, при этом мы еще должны понимать, что означает в записях каждый символ: скобки, буквы, числа. Что мы понимаем под буквами a и b? Что представляет собой выражение в скобках? Что показывает число 3?

Чем является скобка по отношению к числу 3?

Предлагаю в группах обсудить вопрос:

- Какие факты о степенях и многочленах можно использовать для того, чтобы возвести в куб сумму и разность двух выражений? Можно предложить схему-модель. 2 минуты.

Версии : 1.Применить определение степени: (a +b)³=(a +b) (a +b) (a +b) =…

(a - b)³=(a - b) (a - b) (a - b) =…

А где же рациональность решения данного вопроса?

2.Применить формулу «квадрат суммы и квадрат разности двух выражений» (a +b)³=(a +b) (a +b)² =… (a -b)³=(a - b) (a - b)² =…

Какие интересные версии!

А теперь предлагаю в группах отработать наши версии: выполнить определенные действия над многочленами (т.е. провести небольшое исследование). Для этого распределите роли в группах: определитесь, кто у вас будет руководителем группы, секретарем, который будет писать все умные мысли, голос группы - тот кто будет выступать от группы, хранитель времени, остальные -советчиками.

Разверните ватманы с уже имеющимися записями вашими версиями и завершите вывод формулы: пишем крупным шрифтом. Время 5 минуты.

Группа №1 (a +b)³=(a +b) (a +b) (a +b) =…

Группа №2 (a - b)³=(a - b) (a - b) (a - b) =…

Группа №3 (a +b)³=(a +b) (a +b)²=…

Группа №4 (a - b)³=(a - b) (a - b)²=…

Выступление от групп. Ватманы вывешивают на доску.

- Какие факты использовали при решении?

А теперь откройте учебник 7 кл., но другого автора - Юрия Николаевича Макарычева п. 32 с.155. Воспользуйтесь закладкой. Прочитайте до примера 5. Какую идею вывода формул предложил Ю.Н.Макарычев? Сравните свои результаты с формулами в учебнике. Правильно ли вы вывели формулы? Как по-другому называют ФСУ? (тождествами)

На экране появляются формулы: (a +b)³=a³+3a²b+3ab²+b³

(a - b)³= a³-3a²b+3ab²-b³

Запишите формулы в тетради.

Теперь важно грамотно прочитать эти формулы. Поработайте в парах. Проговорите тождества поочередно друг другу. При необходимости читайте текст в выделенных рамочках. Замечательно! А теперь хором. (Слайд).

Но это еще не все! Что бы формулы хорошо запоминались, надо учиться анализировать их. Давайте проанализируем новые ФСУ.

Работа в парах. «Щадящий опрос»:

• Что собой представляет правая часть формулы? (многочлен стандартного вида)

• Из чего состоит многочлен? (из суммы одночленов)

• Какой степени каждый член многочлена? (третьей).

• А какие коэффициенты содержаться внутри формулы?

• Что происходит с показателем степени первого слагаемого, с показателем степени второго слагаемого при чтении многочлена?

• Чем отличается формула кубов суммы от куба разности?

Вот и все секреты запоминания формул. А теперь вернемся к началу урока.

Найдите ошибки в последнем 6 задании. (слайд)

4.Физкультминутка. Мультимидийная презентация. Или…

Мы топаем ногами,

Мы хлопаем руками,

Киваем головой,

Мы руки поднимаем,

Мы руки опускаем,

Их другу подаем.

Мы глазки вверх подняли

И тут же опустили,

Глядим по сторонам.

Немного поморгали,

Немного покрутили -

И снова за дела!

5.Формирование умений и навыков.

«Мало иметь хороший ум, главное -хорошо его применять» Рене Декарт (слайд)

- Где применяют ФСУ?

• При преобразовании выражений

• При упрощении выражений и нахождении его значений

• При решении уравнений Задание №42E787 Решите уравнение (x+3)³=9(x+3).

• При решении текстовых задач

• При доказательствах тождеств

Запишите в тетрадях №827(а) (слайд)

• Как с помощью формулы СУ преобразовать куб суммы?

• Кто желает комментировать с места?

(a+2)³ = a³+3a²2 +3a2² +2³ = а³+6а²+12а+8

• Что представляет собой выражение a³+3a²2 +3a2² +2³?

• Этот многочлен стандартного вида?

• Как привести его к стандартному виду?

№828(а) самостоятельно.

(b-4)³ = b³- 3b²4 +3b4² - 4³ = b³- 12а² + 48b - 64 Кто решил -поднимите руку. Дима освободился. Кому нужна помощь в группе поднимите руки? Кто решил первым из группы после проверки становится консультантом в своей группе.

Освободившиеся дорешивают номера №827, №828

Первичный контроль знаний. «Светофор». Устная работа с сигнальными кругами.

Используя формулу куба суммы или куба разности, преобразуйте выражение

в многочлен стандартного вида и выберите правильный ответ.

№ 1. (x + у)³ =

+

№2.

-3

- 3 +

+3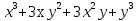

№3 .=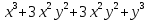

27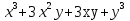

27 +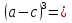

27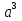

№4 =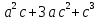

+

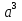
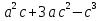
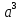Вспомним , ребята, какие цели мы ставили в начале урока? Поднимите руки кому удалось их достичь?

Название какого государства скрывается в математическом выражении a³ ?

А известна ли вам столица Кубы? (Гавана)

7. Рефлексия. Выразите свое мнение по отношению к себе, к уроку, дополняя любое из предложений.

8. Спасибо, ребята, за эмоции, которые вы нам подарили, за грамотные ответы, желаю вам успехов в дальнейшем. Спасибо за урок.

Анализ урока.

ТЕМА: «Формулы сокращенного умножения»

Цели урока:

• Образовательные:

  • проверка усвоения формул «квадрат суммы и разности двух выражений» «разность квадратов», «сумма и разность кубов»;

  • вывод формул «куб суммы и разности двух выражений» умение применять их при преобразованиях выражений с целью упрощения.

• Развивающие:

  • Развитие умения ставить цели

  • развитие умения сравнивать, анализировать, обобщать, делать выводы, правильно формулировать и излагать мысли;

  • развитие интереса к предмету через содержание учебного материала, расширение кругозора.

• Воспитательные:

  • воспитание навыков самоконтроля и взаимоконтроля;

  • воспитание культуры общения, умения работать в парах, группе коллективе, взаимопомощи;

воспитание внимательности, таких качеств характера как настойчивость в достижении цели, умение не растеряться в проблемных ситуациях.