Лекция по электротехнике по теме Цепи переменного тока с активным сопротивлением, индуктивностью и емкостью

Лекция № 9

Тема1.3.Основные положения теории переменного тока. Цепи переменно тока

План

1. Цепи переменного тока с активным сопротивлением, индуктивностью и емкостью.

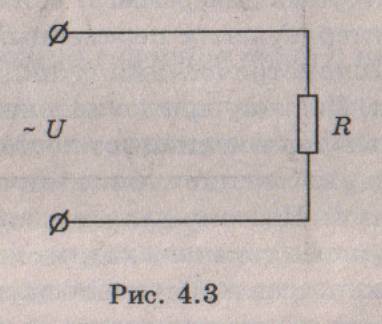
1.Цепь переменного тока с активным сопротивлением. Рассмотрим цепь (рис, 4,3), в которой к активному сопротивлению (резистору) приложено синусоидальное напряжение:

Тогда по закону Ома ток в цепи будет равен:



Мы видим, что ток и напряжение совпадают по фазе. Векторная диаграмма для этой цепи приведена на рис. 4.4, а зависимости тока и напряжения от времени (временная диаграмма) - на рис. 4.5:

Выясним, как изменяется со временем мощность в цепи переменного тока с резистором.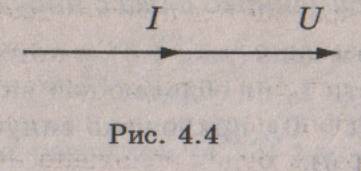

Мгновенное значение мощности равно произведению мгновенных значений тока и напряжения:

Из этой формулы мы видим, что мгновенная мощность всегда положительна и пульсирует с удвоенной частотой (рис4.5). I,U,p .

Это означает, что электрическая энергия необратимо превращается в теплоту независимо от направления тока в цепи.

Те элементы цепи, на которых происходит необратимое преобразование электрической энергии в другие виды энергии (не только в теплоту), называются активными сопротивлениями. Поэтому резистор представляет собой активное сопротивление.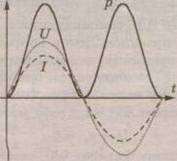

Цепь переменного тока с индуктивностью. Рассмотрим цепь (рис. 4.6), в которой к катушке индуктивности L, не обладающей активным сопротивлением (R = 0), приложено синусоидальное напряжение (4.6).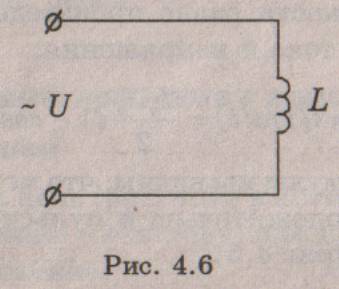

Протекающий через катушку переменный ток создает в ней ЭДС самоиндукции , которая в соответствии с правилом Ленца направлена таким образом, что препятствует изменению тока. Другими словами, ЭДС самоиндукции направлена навстречу приложенному напряжению. Тогда в соответствии со вторым правилом Кирхгофа можно записать:

(4.9)

Согласно закону Фарадея ЭДС самоиндукции

(4.10)

Подставив (4.10) в (4.9), получим:

Решение этого дифференциального уравнения имеет вид:

(4.12), где (4.13)

Деля обе части равенства (4.13) на , получим для действующих значений

(4.14)

Соотношение (4.14) представляет собой закон Ома для цепи с идеальной индуктивностью, а величина называется индуктивным сопротивлением. Индуктивное сопротивление измеряется в омах.

Мгновенная мощность в цепи с чисто индуктивным сопротивлением равна:

(4.15)

Положительные значения мощности соответствуют потреблению энергии катушкой, а отрицательные - возврату запасенной энергии обратно источнику. Средняя за период мощность равна нулю. Следовательно, цепь с индуктивностью мощности не потребляет - это чисто реактивная нагрузка. В этой цепи происходит лишь перекачивание электрической энергии от источника в катушку и обратно. Индуктивное сопротивление является реактивным сопротивлением.

Цепь переменного тока с индуктивностью и активным сопротивлением. Реальные цепи, содержащие индуктивность, всегда имеют и активное сопротивление: сопротивление провода обмотки и подводящих проводов. Поэтому рассмотрим электрическую цепь (рис. 4.9), в которой через катушку индуктивности L, обладающую активным сопротивлением R, протекает переменный ток

(4.16)

Через катушку и резистор протекает один и же ток, поэтому в качестве основного выберем вектор тока и будем строить вектор напряжения, приложенного к этой цепи.

Напряжение, приложенное к цепи, равно векторной сумме падений напряжений на катушке индуктивности и на резисторе:

(4.17)

Напряжение на резисторе, как было показано выше, будет совпадать по фазе с током: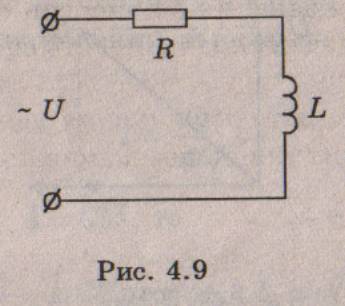

(4.18)

а напряжение на индуктивности будет равно ЭДС самоиндукции со знаком минус (по второму правилу Кирхгофа):

. (4.19)

Мы видим, что напряжение на индуктивности опережает ток на угол ?/2. Построив векторы и , и воспользовавшись формулой (4.17), найдем вектор Векторная диаграмма показана на рис. 4.10. Мы видим, что в рассматриваемой цепи ток I отстает по фазе от приложенного напряжения U, но не на / 2, как в случае чистой индуктивности, а на некоторый угол . Этот угол может принимать значения от 0 до ? / 2 и при заданной индуктивности зависит от значения активного сопротивления: с увеличением R угол уменьшается.

Как видно из векторной диаграммы, модуль вектора равен

, где величина называется полным сопротивлением цепи.

Сдвиг по фазе между током и напряжением данной цепи также определяется из векторной диаграммы:

(4.22)

Цепь переменного тока с емкостью Рассмотрим электрическую цепь, в которой переменное напряжение (4.6) приложено к емкости С.

Мгновенное значение тока в цепи с емкостью равно скорости изменения заряда на обкладках конденсатора:

; но поскольку q = СU, то

, где (4.25)

Мы видим, что в этой цепи ток опережает напряжение на 2. Переходя в формуле (4.25) к действующим значениям переменного тока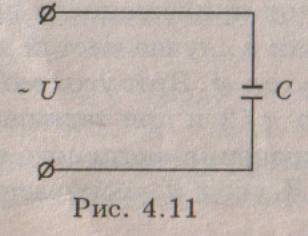

) , получим: (4.26)

Это закон Ома для цепи переменного тока с емкостью, а величина - называется емкостным сопротивлением. Векторная диаграмма для этой цепи показана на рис. 4.12, а временная - на рис. 4.13

Мгновенная мощность в цепи, содержащей емкость:

(4.27)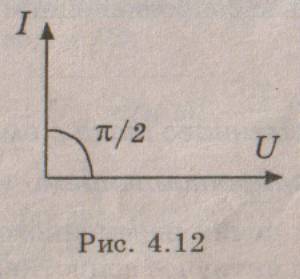

Мы видим, что мгновенная мощность изменяется с удвоенной частотой (рис. 4.13). При этом положительные значения мощности соответствуют заряду конденсатора, а отрицательные - его разряду и возврату запасенной энергии в источник. Средняя за период мощность здесь равна нулю, поскольку в цепи с конденсатором активная мощность не потребляется, а происходит обмен электрической энергией между конденсатором и источником. Следовательно, конденсатор так же, как и индуктивность, является реактивным сопротивлением.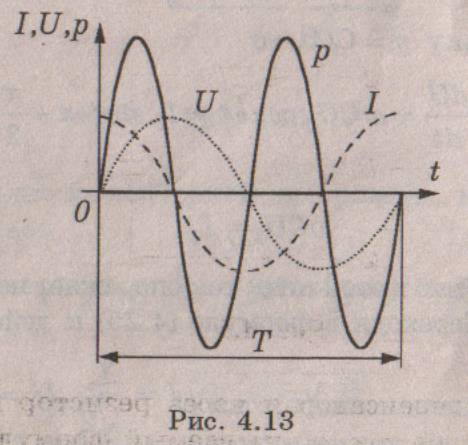

Вопросы для самопроверки:

1. Дать определение понятию « Активное сопротивление».

2. Выразить закон Ома для цепи переменного тока с активным сопротивлением.

3. Дать определение понятию « Индуктивность».

4. Выразить закон Ома для цепи переменного тока с индуктивностью.

5. Дать определение понятию « Емкость».

6. Описать основные параметры цепей переменного тока с активным сопротивлением, индуктивностью и емкостью.

7. Дать определение понятию « Активное сопротивление».

8. Дать определение понятию « Индуктивность».

9. Выразить закон Ома для цепи переменного тока.