И.А. Морев, Л.Я. Морева, А.А. Мойся, А.С. Чернышов ОПРЕДЕЛЕНИЕ ЧИСТОПОРОДНОСТИ ПО КОМПЛЕКСУ МОРФОМЕТРИЧЕСКИХ ПРИЗНАКОВ

И.А. Морев, Л.Я. Морева, А.А. Мойся, А.С. Чернышов

ОПРЕДЕЛЕНИЕ ЧИСТОПОРОДНОСТИ ПО КОМПЛЕКСУ МОРФОМЕТРИЧЕСКИХ ПРИЗНАКОВ

Проводимые на территории юга России исследования показывают, что в результате неконтролируемого завоза и кочёвок пасек в период медосбора, произошло смешивание генотипов пчёл и образование метисированных форм.

Ряд работ показали, что методами многомерной статистики возможна породная идентификация, но необходим метод выявления метисированных форм на пасеках в целях поддержания чистопородности, и тем самым интенсификации их искусственного воспроизводства [1].

В данном исследовании обучающей совокупностью являлись выборки трех чистых пород пчел и двух метисированных, описанных по комплексу морфометрических признаков.

Ориентация именно на комплекс признаков, формирующих одну систему - морфотип пчелы, уже убедительно обоснована в большом ряде исследований на различных биологических объектах. Общий их итог вполне определенно сформулирован в тезисе А.В. Яблокова [3]: переход от анализа изменчивости единичных признаков к их коррелированным комплексам увеличивает генетическую мощность исследования фенотипической изменчивости.

</ Материалом для исследований послужили выборки пчел по 50 особей чистопородных пчел Краинской породы (Apis mellifera carnica),Карпатской породы (Apis mellifera carpatica), серой горной кавказской (Apis mellifera caucasica) и две выборки метисированных форм.

В работе анализировали следующие морфометрические признаки: длина хоботка; длина переднего крыла; ширина переднего крыла; длина заднего крыла; ширина заднего крыла; тарзальный индекс; ширина третьего тергита; кубитальный индекс крыла; количество зацепок; гантельный индекс; дискоидальное смещение.

Задача идентификации породной принадлежности или выявление сильно метифированных пчел предполагает их сопоставление не по отдельным признакам, а по морфотипу в целом. Иными словами, необходимо объединить исходный комплекс морфометрических признаков в единую меру - их линейную комбинацию. Решать эту задачу в рамках дискриминантного анализа. Данный метод напрямую предназначен для изучения межгрупповых различий. Он позволяет строить линейные комбинации признаков - дискриминанатные функции и, при этом, минимизирует внутригрупповую изменчивость, мешающую объективной оценке групп. [2].

Дискриминантный анализ позволяет решать несколько задач межгруппового сравнения. К одной из них относится выбор информативного комплекса признаков - такого набора переменных, которые играют наибольшую роль в межгрупповых различиях. Следует отметить, что для определенных условий среды и изучаемых групп этот комплекс может быть различным, именно по этой причине сравнение проводится на всех морфометрических признаках. Результат пошагового анализа представлен в таблице 1.

Таблица 1 - Результаты пошагового дискриминантного анализа

(информативный комплекс признаков)Примечание. Wilks' Lambda - лямбда Уилкса; Partial Lambda - частная лямбда Уилкса; F-remove - значение F-критерия, связанное с соответствующей частной лямбдой Уилкса; p-level - уровень значимости критерия F-remove; 1-Toler. (R-Sqr.) - толерантность - мера избыточности переменной в модели.

Как видно по уровню значимости в группу информативных признаков в плане различения чистых пород и метисов пчел вошли: длина хоботка, длина большого крыла, ширина большого крыла, зацепки крыла, тарзальный индекс, кубитальный индекс крыла %, дискоидальное смещение крыла, гантельный индекс.

В последующих колонках таблицы представлены статистики в той или иной мере характеризующие относительную ценность каждой переменой в межгрупповых различиях. Сюда относятся: лямбда Уилкса, частная лямбда, значения F-критерия, значения вероятности ноль-гипотезы об отсутствии роли переменной и значения толерантности. Ценность той или иной переменной можно определить, в частности, по минимальным значениям частной лямбды и минимальным значениям толерантности (1-R2) или максимальным значениям собственно R2=1-Tolerance.

Расстояния между центрами групп (популяций) в пространстве дискриминантных функций называются расстояниями Махаланобиса и представляют собой наиболее точную оценку межпородных различий, определяемых на фоне минимизированной внутригрупповой дисперсии таблица 2.

Таблица 2 - Расстояния (Махаланобиса) между центрами пород пчел и метисов в пространстве дискриминантных функцийПорода

Карника

Карпатская

Серая горная кавказская

Помесные А

Помесные Б

Карника

2,13

11,5

13,78

5,49

Карпатская

0,00

9,73

10,21

2,51

Серая горная кавказская

0,00

0,00

6,31

4,58

Помесные А

0,00

0,00

0,00

6,00

Помесные Б

0,00

0,00

0,00

0,00

Примечание. Выше главной диагонали матрицы приведены расстояния Махаланобиса, ниже - вероятность нуль-гипотезы об отсутствии различий между чистопородными и помесными.

Расчет расстояний Махаланобиса подтверждает следующее: наиболее велики расстояния от всех чистых пород помесные пчелы группы А. Помесные пчелы группы Б более близки Карпатской породе (расстояние 2,51 усл.ед.), хотя между ними различия статистически достоверны.

В ходе исследования для более наглядного представления был построен 3D - график средних значений линейных комбинаций в пространстве трех дискриминантных функций рисунок.

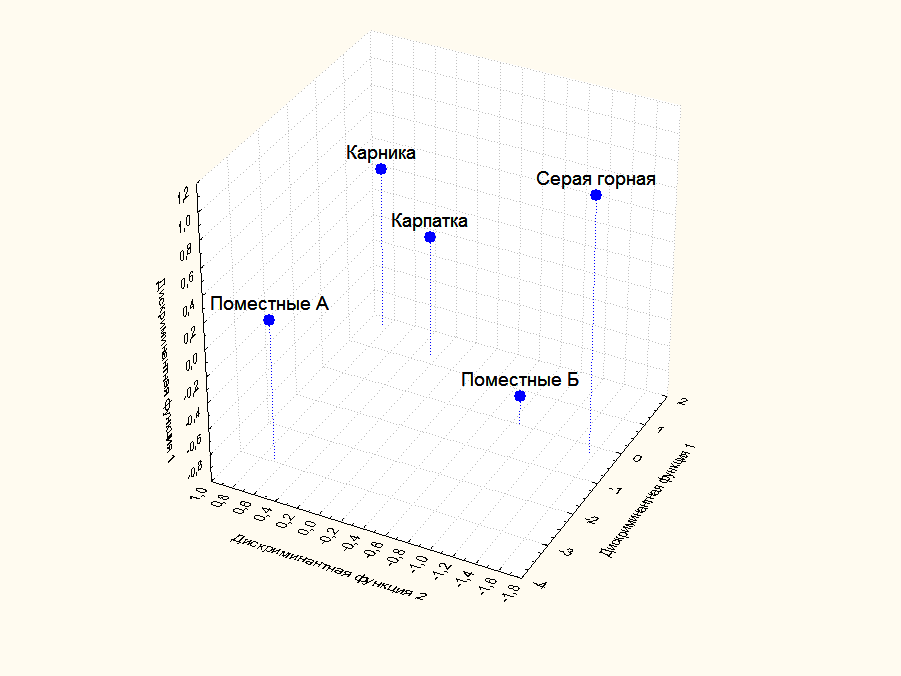
Рисунок - график средних значений линейных комбинаций в пространстве трех дискриминантных функций

Таки образом, можно сделать вывод о том, что предлагаемый алгоритм анализа комплекса морфометрических признаков позволяет проводить идентификацию породной принадлежности выборок из популяций, чье происхождение неизвестно и относительно точно определять чистопородность, отделяя сильно метесированные формы.

Использованные источники

1. Морева Л.Я., Морев И.А. Изменение морфометрических признаков медоносной пчелы на Северо-Западном Кавказе // Пчеловодство (научно-производственный журнал). 2012. № 3. С. 10-11.

2. Тюрин В. В. , Морев И.А. ,Волчков Ю.А. Дискриминантный анализ в селекционно - генетических исследованиях, Краснодар, 2003 . 24 с.

3. Яблоков А. В. Фенетика. М.,1980 . с 132 .