- Учителю
- Разработка урока 'Событие как множество, элементы которого-элементарные исходы' (закономерности окружающего мира7 класс)
Разработка урока 'Событие как множество, элементы которого-элементарные исходы' (закономерности окружающего мира7 класс)
Закономерности окружающего мира - 7 класс
Тема 8. Алгебра событий
Задачи темы: а) познакомить учащихся с алгеброй событий, вспомнить, что математические действия выполняются над буквами, если буквами обозначены числа;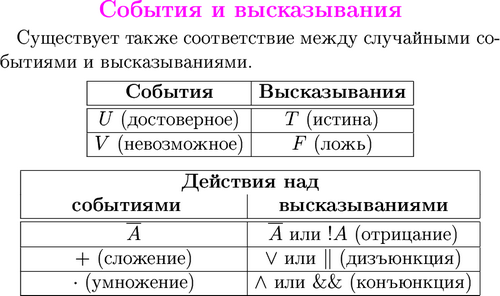
б) ответить на вопрос: разве можно выполнять алгебраические действия над буквами-событиями?
в) в ходе беседы с семиклассниками использовать такие понятия, как «сумма событий» и «произведение событий»; знать, что в алгебре событий существуют переместительные, сочетательные, распределительные и другие законы;
г) разъяснить учащимся, что пользуясь алгеброй событий можно вычислить вероятность события, представляя его как сумму или поизведение других событий, вероятность которых известна или может быть надежно измерена.
урок 01(01). Событие как множество, элементы которого - элементарные исходы.
Задачи урока: а) в ходе беседы с учащимися дать понятие о событии как множестве, элементами которого являются элементарные исходы; б) познакомить семиклассников с новыми понятиями: «универсальное множество», «множество», «элементы множества», «бесконечные множества», «математическая логика»; в) развивать логику математического мышления.
Оборудование урока: таблицы, картины, иллюстрирующие событие как множество
Эпиграф: Пользуясь алгеброй событий, можно вычислять вероятность события, представляя ее как сумму или произведение других событий, вероятность которых известна или может быть надежно измерена. (Вопросы и ответы)
Математическая логика есть по предмету, математика по методу.
(П. Порецкий, российский математик)
Содержание урока:
-
Организация школьников на урок.
-
Изучение нового материала.
-
Тезисы урока:
-
Вступительное слово учителя. Мы продолжаем, ребята, знакомиться с закономерностями окружающего нас мира. В предстоящем учебном году вместе повторим, что знаем и продолжим получать знания по предмету. Мы помним основные понятия:
- случайное событие;
- левое и правое;
- симметрия и ассиметрия;
- геометрическая симметрия;
- перестановки, сочетания, шансы;
- вероятность;
- частота.
В этом учебном году познакомимся со следующими понятиями;
- алгебра событий и основные правила вычисления вероятностей;
- полная вероятность ;
- вероятности гипотез;
- математическая схема Бернулли;
- случайные величины.
-
Сегодня мы с вами поговорим о событии как множестве. Будем рассматривать события, которые происходят при двукратном бросании игрального кубика. Об этой ситуации мы говорили достаточно подробно, где объясняли, что представляет собой пространство элементарных исходов. Называют его универсальным множеством. В данном рассматриваемом случае универсальное множество состоит из 36 элементарных исходов. Понятно, что вероятность каждого исхода равна 1/36. Графически эти исходы будут использоваться нами и в данной теме. Напомню, что например, 35 - это не тридцать пять, а три-пять (это элементарный исход с выпадением грани 3 в первом бросании кубика и грани 5 во втором бросании). Прошу вас обратить внимание на то, что в дальнейшем будем разделять дефисом очки выпавших пар граней: 1 - 1, 1 - 2 , ... (чтобы избежать путаницы).
-
А сейчас работаем с рисунками учебника. На рис. 1 в таблице 32 вы видете в виде маленьких эллипсов 36 элементарных исходов испытаний с двукратным бросанием кубика (рассмотрите и найдите их в таблице). Обрати внимание, что там же выделены области , соответствующие шести выбранным в качестве примера событиям: A, B, C, D, E, F. Каждая из этих областей (каждое из шести событий) состоит из определенного набора элементарных исходов. Сделаем вывод: каждое событие есть множество, элементами которого являются соответствующие элементарные исходы.
-
Понятие множества широко используется в математике. Множеством называют любой набор предметов, объектов, фигур, свойств, а также событий, собранных по какому-либо признаку (или признакам). Все эти предметы, объекты, фигуры, свойства события называются элементами множества.
-
Множества с конечным числом элементов называют конечными множествами. Существуют также бесконечные множества (например, множество всех натуральных чисел). Запомните, рассматривая алгебру событий, мы с вами фактически рассматриваем алгебру множеств или множеств событий.

-
Обратимся к истории появления алгебры событий. Замечу, что алгебра событий существенно отличается от алгебры чисел. Но и во многом можно найти между ними аналогии. Последнее неудивительно, поскольку алгебра чисел и алгебра множеств (событий) имеют общие корни в математической логике. Рождение математической логики во многом связано с идеями знаменитого немецкого ученого Готфрида Вильгельма Лейбница (1646 - 1716), считавшего что различные рассуждения могут быть в каком-то смысле сведены к механическому выполнению определенных действий по некоторым правилам. Как самостоятельный раздел математики математическая логика начала формироваться с середины XIX века благодаря работам ирландского математика и логика Джорджа Буля (1815 - 1864).

Буль применил алгебраические методы для решения логических задач и сформулировал на языке алгебры некоторые фундаментальные законы мышления. Они фактически моделируют алгебру Буля.
-
Но вернемся к рисунку учебника и рассмотрим шесть событий - множеств.
Событие А - выпала пара одинаковых граней. Оно представлено множеств, элементами которого являются шесть элементарных исходов: 1 - 1, 2 - 2, 3 - 3, 4 - 4, 5 - 5, 6 - 6. Вероятность этого события P(A) = 6 / 36.
Событие C - выпала пара граней с суммой очков меньше 8; множество с остоит из 21 элемента. Вероятность события P(C) = 21 / 36.
Событие B - выпала пара граней, среди которых есть хотя бы одна единица. В этом множестве 11 элементов (6 - 1, 5 - 1, 4 - 1, 3 - 1, 2 - 1, 1 - 1, 1 - 2, 1 - 3, 1 - 4, 1 - 5, 1 - 6). Вероятность события P(B) = 11 / 36.
Событие D - выпала пара граней с суммой очков больше 7; множество состоит из 15 элементов. Вероятность события P(D) = 15 / 36.
Событие E - выпала пара граней с суммой очков 10; множество состоит из трех элементов. Вероятность события P(E) = 3 / 36.
Событие F - выпала пара граней с очками 5 и 5; множество состоит из одного элемента (элементарного исхода 5 - 5). Вероятность события P(F) = 1 / 36.
-
Работа с текстом учебника на с.205: понятие «противоположное (дополнительное) событие». Разбираются примеры таких событий.
-
В теории множеств используется понятие подмножества (части множества). Множество К называют подмножеством множества L, если каждый элемент множества К является одновременно элементом множества L. Записывают это так: K c L. Или L c К.Однако заметим, что если бы при этом каждый элемент множестваL являлся одновременно элементом множества К, то оба множества считались бы равными: К = L. Делаем вывод: если К c L и L c M, то К c M. А теперь обратимся к таблице 32. Отметим, что BcC,Ec D,F c E,F c D. Примечание: в случае F и E, F и D знак «c» обращен в обратном порядке; L c K тоже обращен в обратном порядке.
-
Итог урока.
-
Мы узнали, что Вероятность - свойство случайных событий.
-
Понятие события - первичное понятие теории - строго не определяется.
-
Событие - это то, что при определенных условиях может произойти или не произойти. В общем случае событие - это множество элементов. (Иногда - один, иногда - бесконечное множество)
-
Познакомились с понятием «подмножество», научились записывать множество по отношению к подмножества, выяснили историю появления математической логики.
-
Домашнее задание: §8.1, упражнение 1, с. 220
ЗОМ - 7 класс
урок 02(02). Несовместные и совместные события.
Задачи урока: а) в ходе беседы с семиклассниками выяснить значения понятий «несовместные» и «совместные» события; б) научить решать задачи с изученными понятиями.
Оборудование урока: плакат для устных вычислений, карточки с заданиями.
Содержание урока:
-
Организация школьников на урок.
-
Проверка выполнения домашнего задания (рассказы учащихся)
-
Изучение нового материала
-
Вступительное слово учителя. Сегодня мы поговорим о значении понятий «несовместные» и «совместные» события, научимся решать задачи с изученными понятиями. Но прежде вспомним изученные ранее понятия.
-
Совместные и несовместные события.
Два события, которые в данных условиях могут происходить одновременно, называют совместными, а те, которые не могут происходить одновременно, - несовместными.
Например, события «пошел дождь» и «наступило утро» являются совместными, а события «наступило утро» и «наступила ночь» - несовместными.
Пример 1
Условия :
бросаем игральную кость
Событие А :
выпало четное число очков
Событие B :
выпало число очков меньше, чем 4
Событие AB :
выпало 2 очка
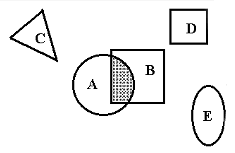
Пример 2. См. рисунок 1.2.
Событие А :
круг
Событие B :
квадрат
Событие AB :
заштриховано
Рисунок 1.2
Если СЕ = V, т.е. пересечение С и Е - пустое множество, события С и Е не имеют общих элементов, то такие события называются несовместными.
На рисунке - несовместные события С, Е, D.
В упражнениях 7-9 среди данных пар событий указать, какие являются совместными, а какие - несовместными.
7. В сыгранной Катей и Славой партии в шахматы: 1) Катя выиграла, Слава проиграл; 2) Катя проиграла, Слава выиграл.
8 . Брошена игральная кость. На верхней грани оказалось: 1) 6 очков, 5 очков; 2) 6 очков, четное число очков.
9 . Из набора домино вынута одна костяшка, на ней: 1) одно число очко больше 3, другое число 5; 2) одно число не меньше 6, другое число не больше 6; 3) одно число 2, сумма обоих чисел равна 9.
Упражнения для самостоятельного решения (на каждой парте тексты с заданиями)
-
Из событий: 1) «идет дождь»; 2) «на небе нет ни облачка»; 3) «наступило лето»; - составить всевозможные пары и выявить среди них пары совместных и пары несовместных событий.
-
Из событий: 1) «наступило утро»; 2) «сегодня по расписанию 6 уроков»; 3) «сегодня первое января»; 4) «температура воздуха в Салехарде + 20°С» - составить всевозможные пары и выявить среди них пары совместных и пары несовместных событий.
-
Имеется правильная треугольная пирамида - тетраэдр. Одна из ее граней серая, а три другие белые. Тетраэдр бросают на стол и наблюдают за гранью, которой он соприкасается со столом. Являются ли равновозможными события «тетраэдр упал на серую грань» и «тетраэдр упал на белую грань»?
-
Бросается игральный кубик, у которого: 1) 2 грани; 2) 3 грани - окрашены в красный цвет, а остальные - в желтый. Являются ли равновозможными события «выпала желтая грань» и «выпала красная грань»?
-
Из полной колоды в 36 карт наугад вынимается одна карта. Являются ли равновозможными события: 1) «вынута карта красной масти» и «вынута карта черной масти»; 2) «вынут король» и «вынута дама»; 3) «вынута карта бубновой масти» и «вынута карта червовой масти»; 4) «вынута карта пиковой масти» и «вынута карта красной масти»; 5) «вынута шестерка треф» и «вынута дама пик»?
-
Из полной колоды карт вынимается одна карта. Выяснить, являются совместными или несовместными события: 1) «вынута карта красной масти» и «вынут валет»; 2)»вынут король» и «вынут туз».
IV. Итог урока.
Повторить определения всех видов событий (желательно со своими примерами)
V. Домашнее задание:
Придумать примеры (для соседа по парте) со всеми изученными видами событий.
© 2003-2009 Издательский дом «Первое сентября»
![]()
Пример 1
Пример 2
Условия :
бросаем игральную кость
стрела попала в мишень
Событие А :
выпало четное число очков
стрела попала в "десятку"
Мн-во элементов А :
2, 4, 6
бесконечное множество точек, заполняющих "десятку"
Событие, которое нельзя разбить на элементы называется элементарным.
В примере 1 - это выпадение определенной грани, скажем - 4.
Пример 3
Условия :
бросаем игральную кость
Событие А :
выпало четное число очков
Событие B :
выпало число очков меньше, чем 4
Событие A + B :
выпало 1, 2, 3, 4 или 6 очков
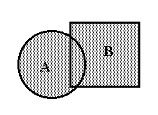
Пример 4. См. рисунок 1.1.
Событие А :
круг
Событие B :
квадрат
Событие A + B :
заштриховано
Рисунок 1.1
Событие, которое в данных условиях всегда происходит называется достоверным (U)
В примере 1 - это выпадение любой грани.
Событие, которое в данных условиях никогда не происходит называется невозможным (V)
В примере 1 - это одновременное выпадение двух или более граней при однократном бросании одной кости.
Рассматривая события как множества, можно определить действия над событиями.
a . Объединение событий или сумма событий A U B или А + В - событие, содержащее все элементы А и В
b . Пересечение событий или произведение событий - A B или АВ - событие, содержащее только общие элементы А и В
c . Говорят, что событие А влечет за собой событие В (обозачение А c В), если, когда происходит A, то B обязательно происходит , т.е. все элементы А входят и в В, но В может содержать и элементы, не входящие в А.
Пример 7
Пример 8. См. рисунок 1.2.
Условия :
бросаем игральную кость
Событие А :
выпало два очка
На рисунке 1.2 AB c B
Событие B :
выпало четное число очков
Элементы А входят в В, или A c B
Если А c В и одновременно В c А, т.е. все элементы у А и В - общие, то такие события называются равносильными, или равными.
d . Все элементарные события, в сумме составляющие достоверное образуют пространство элементарных событий. При однократном бросании одной кости пространство элементарных событий содержит 6 элементов, при одновременном бросании двух костей - 36 элементов (всевозможные сочетания числа очков на первой и второй кости), при попадании стрелы в мишень пространство элементарных событий содержит бесконечное множество точек мишени. На рисунках 1 и 2 пространство элементарных событий (достоверное событие) условно обозначено прямоугольником, ограниченным тонкой черной линией и, следовательно содержит все точки этого прямоугольника.
e . Событие, дополняющее данное (А) до достоверного, называется противоположным данному и обозначается чертой сверху (A). Т.е. А + А = U.
f . Попарно несовместные события, в сумме составляющие достоверное образуют полную группу событий.
Пример 9
Условия :
Двое играют шахматную партию. Прошло 2 часа от ее начала.
Полная группа событий :
А - выиграл первый, В - выиграл второй, С - ничья, D - партия еще не закончена.
Прежде, чем определить вероятность на данном пространстве элементарных событий, строят поле событий. Поле событий - это множество событий, которое включает в качестве элементов :
1 . достоверное событие,
2 . невозможное событие,
3 . все элементарные события данного пространства,
4 . все события, которые на этом пространстве можно построить путем сложения (объединения) событий, путем перемножения (пересечения) событий, а также путем взятия противоположных событий от любого уже построенного.
Таким образом, никакая операция алгебры событий над заданным пространством элементарных событий не порождает события, не принадлежащего полю событий. Поле событий может содержать конечное число элементов (если конечно число элементарных событий) или бесконечное множество событий.
Наиболее строгое и общее определение понятия вероятность дал русский математик В.Н. Колмогоров. Оно гласит :
Каждому событию А из поля событий сопоставляется неотрицательное число Р(А), называемое вероятностью этого события и удовлетворяющее следующим аксиомам:
1. Р(А) ≥ 0 ;
2. Р(U) = 1, U - достоверное событие ;
3. Р(А+В) = Р(А) + Р(В) , если А и В - несовместны.
![]()