Решение задач по геометрии ГИА 11 класс 1 часть

Задача №1

Диагональ осевого сечения цилиндра равна 12 см и наклонена к плоскости основания под углом 60º. Найдите площадь боковой поверхности цилиндра.

Решение.

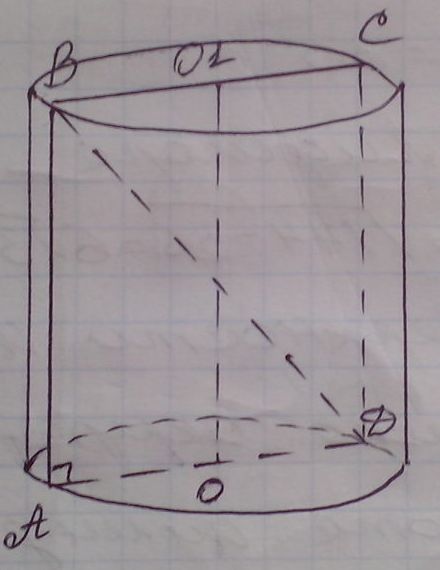
Пусть дан цилиндр, прямоугольник АВСД - его осевое сечение, АД и ВС - диаметры оснований. Точка О - центр нижнего основания, точка - центр верхнего основания. О(АВС), О - высота цилиндра.

АВАД, АД проекция ВД на плоскость нижнего основания цилиндра, тогда ВДА - угол между диагональю ВД и плоскостью нижнего основания.

По условию ВД = 12 см, ВДА = 60º. Из ∆ВАД (ВАД = 90º), АВД = 90º-60º = 30º. АД = ВД, АД = 12 = 6 (см), по свойству катета, лежащего против АВД = 30º.

Используя теорему Пифагора АВ = , АВ = = (см).

Площадь боковой поверхности цилиндра , где C - длина окружности, H - высота цилиндра. Н = АВ = см, , d = AД, ,

Ответ:

Задача №2.

Диагональ осевого сечения цилиндра равна 24см и наклонена к плоскости его основания под углом 30º. Найдите площадь боковой поверхности цилиндра.

Решение.

Пусть дан цилиндр, прямоугольник АВСД - его осевое сечение, АД и ВС - диаметры соответственно нижнего и верхнего оснований. Точка О - центр нижнего основания, точка - центр верхнего основания. О(АВС), О - ось цилиндра, высота цилиндра.

АВАД, АД проекция ВД на плоскость нижнего основания цилиндра, тогда ВДА - угол между диагональю ВД и плоскостью нижнего основания. По условию ВД = 24см, ВДА = 30º. Из ∆ВАД (ВАД = 90º),АВ = ВД, АВ = 24=12(см) - по свойству катета, лежащего против угла 30º.

Используя теорему Пифагора АД = , АД = = 36(см).

Площадь боковой поверхности цилиндра , где C - длина окружности, H - высота цилиндра. Н = АВ = см, , d = AД, ,

Ответ:

Задача №3.

Расстояние от центра основания конуса до середины образующей равно 6 см. Угол между образующей и плоскостью основания равен 60º. Найдите площадь осевого сечения.

Решение.

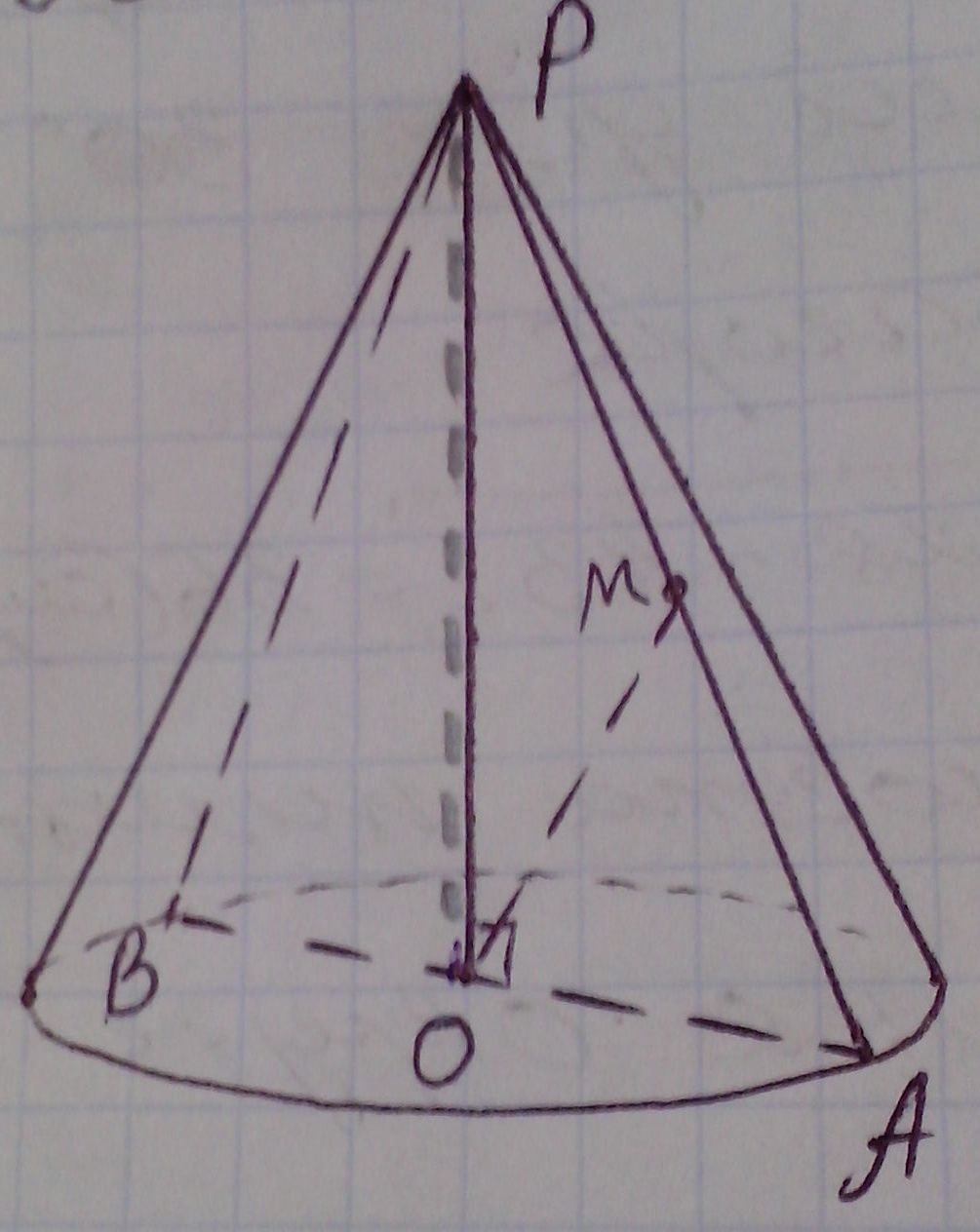
Пусть дан конус, точка О - центр его основания, РО - ось конуса, РО - высота конуса. Построим осевое сечение конуса - равнобедренный ∆АРВ, АВ - диаметр основания конуса, РА=РВ - образующие. Точка М - середина РА, ОМ - расстояние от центра основания конуса до середины образующей РА. По условию ОМ = 6 см. РОАВ, ОА - проекция наклонной РА на плоскость основания конуса, тогда РАО - угол между образующей и плоскостью основания конуса, РАО = 60º.

Из ∆АРВ, РВА = РАВ = 60º, как углы при основании равнобедренного треугольника АРВ, значит ∆АРВ равносторонний, РА = РВ = АВ.

Рассмотрим ∆РОА (РОА = 90º), точка М - середина гипотенузы РА, значит это центр окружности, описанной около ∆РОА, ОМ = АМ = МВ = R, где R - радиус описанной окружности. Тогда РА = 2ОМ, РА = 2·6 = 12 (см).

Площадь осевого сечения , (см²).

Ответ:

Задача №4.

Расстояние от центра основания конуса до образующей равно 3 см. Угол при вершине осевого сечения равен 120º. Найдите площадь осевого сечения конуса.

Решение.

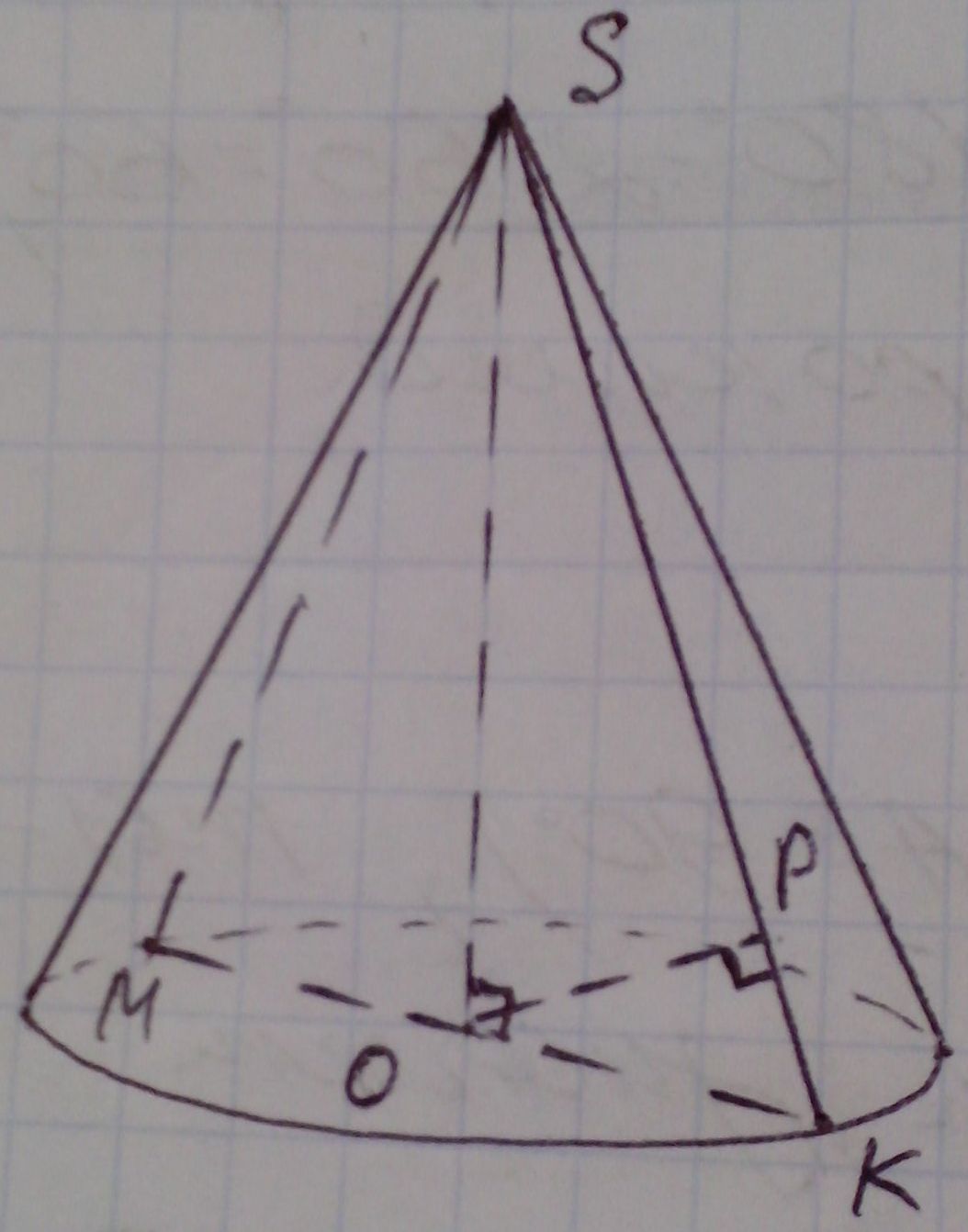
Пусть дан конус, точка О - центр его основания, SО - ось конуса, SО - высота конуса. Построим осевое сечение конуса - равнобедренный ∆МSК, МК - диаметр основания конуса, SМ=SК - образующие конуса, SОМК. Опустим из точки О перпендикуляр на образующую SК, ОРSК, тогда ОР - расстояние от центра основания конуса до образующей SК, ОР = 3 см.

По условию МSК = 120º - угол при вершине осевого сечения. В равнобедренном ∆MSK высота SО - биссектриса, медиана. МSО = КSО = 120º:2 = 60º. Тогда SМК = SКМ = (180º - 120º):2 = 30º - как углы при основании равнобедренного треугольника.

Из ∆SРО (SРО = 90º) SО = , SО = =

Из ∆SОК (SОК = 90º) ОК = SО· tg КSО, ОК = (см), тогда МК = 6·2 = 12 (см). Площадь осевого сечения конуса ,

Ответ:

Задача №5. В основании прямой призмы лежит ромб с большей диагональю, равной 6см. Большая диагональ призмы образует с плоскостью основания угол 30º, меньшая - угол 45º. Найдите объем призмы.

Решение.

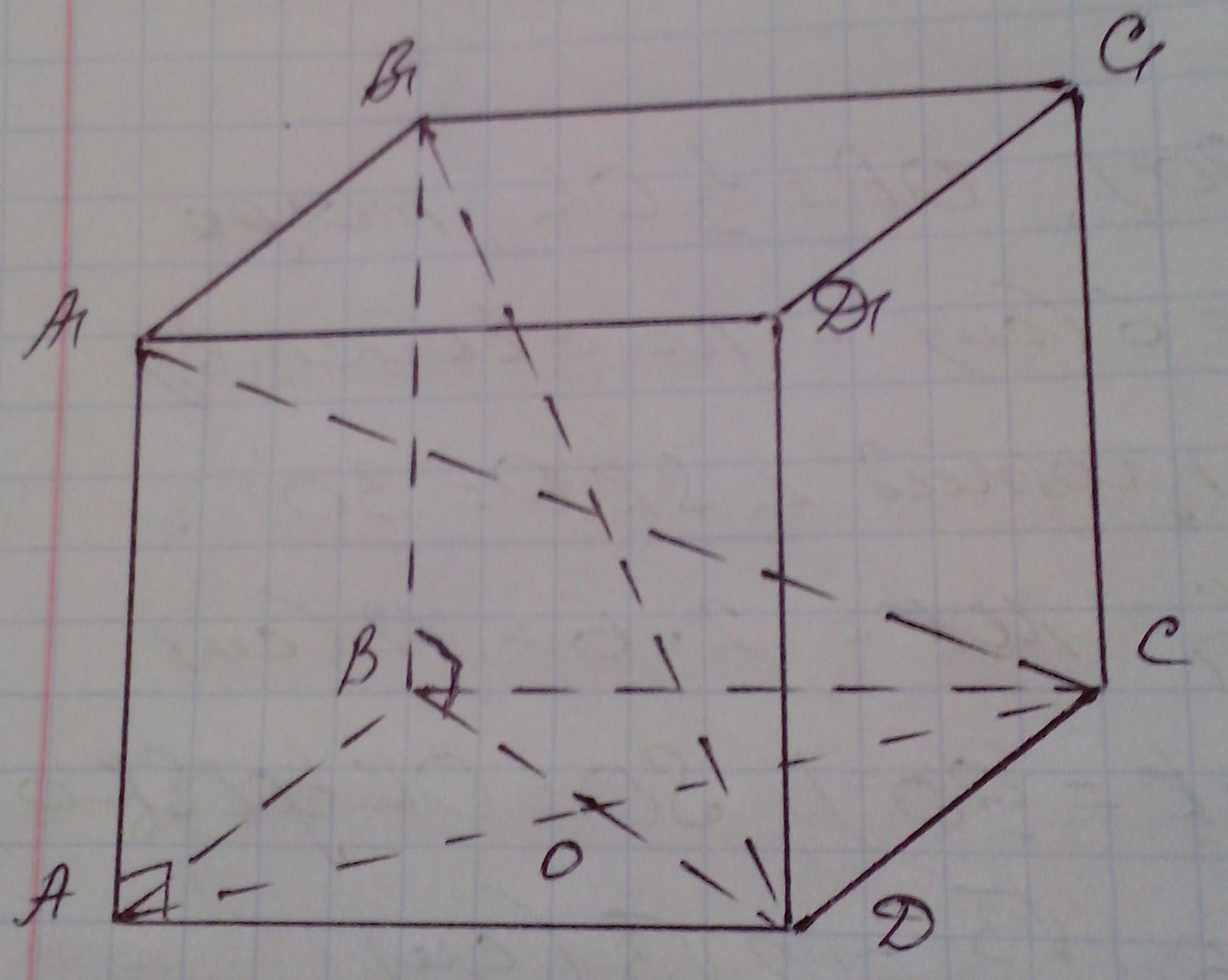
Пусть - прямая призма, ромб АВСД - ее основание. Точка О - точка пересечение диагоналей ромба, А - острый, АС - большая диагональ ромба, ВД - меньшая диагональ ромба, АС > ВД. , АС - проекция на плоскость основания, , ВД - проекция на плоскость основания. Так как АС > ВД, то > по свойству наклонных и их проекций, т.е. - большая диагональ призмы. - угол, образованный большей диагональю призмы с плоскостью основания, - угол, образованный меньшей диагональю призмы с плоскостью основания. По условию =30º, = 45º.

Из ∆, (=90º) АС = 6см, , , .

В ∆, (=90º), = 90º- 45º = 45º, значит ∆ - равнобедренный, ВД = = 6 см.

Объем призмы V = , где - площадь основания призмы, = - высота призмы. , . V = .

Ответ: .

Задача №6.

В основании прямой призмы лежит ромб. Большая диагональ призмы равна 12 см и наклонена к плоскости основания под углом 30º, а меньшая образует с боковым ребром угол 45º. Найдите объем призмы.

Решение.

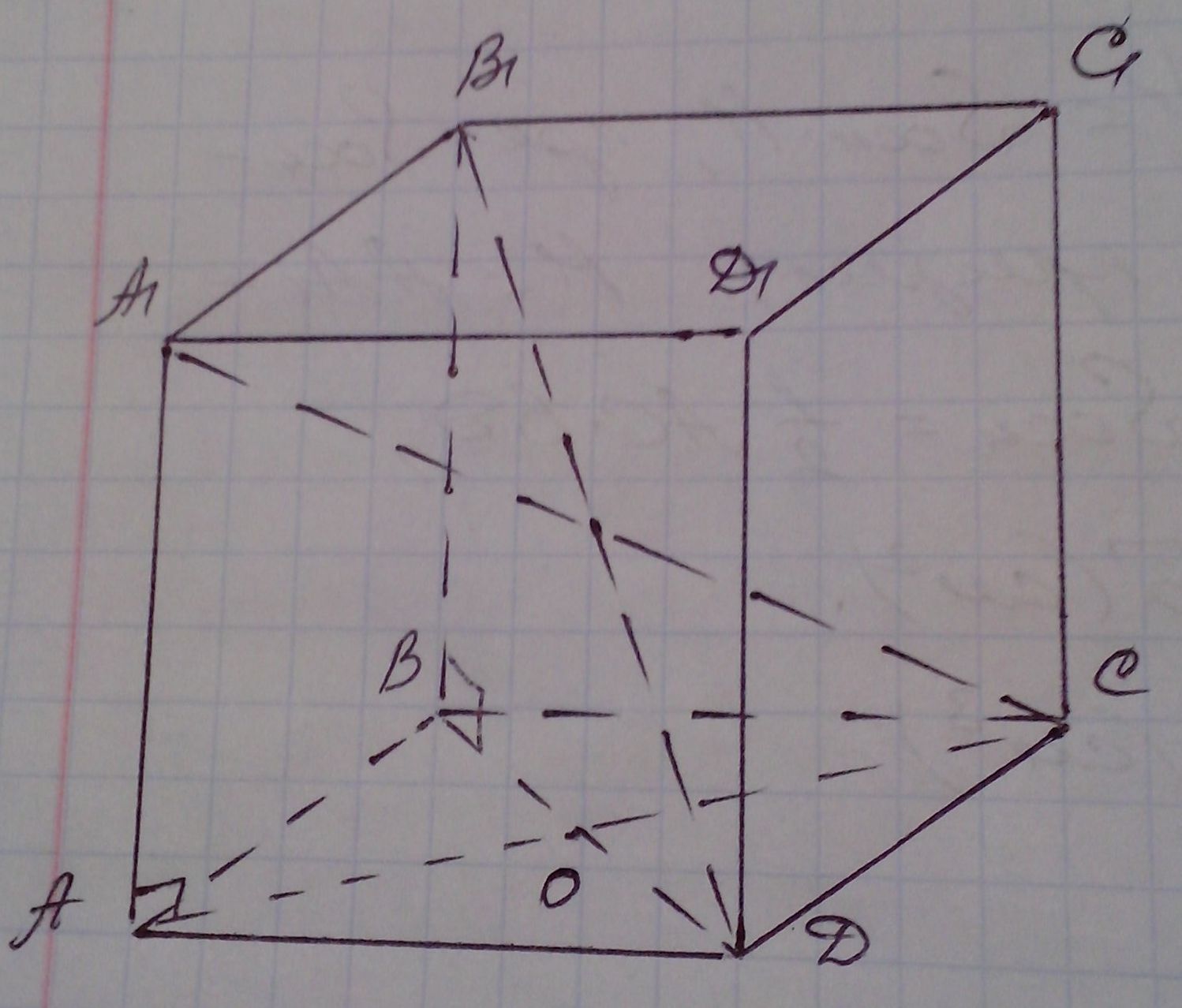
Пусть - прямая призма, ромб АВСД - ее основание. Точка О - точка пересечение диагоналей ромба, А - острый, АС - большая диагональ ромба, ВД - меньшая диагональ ромба, АС > ВД. , АС - проекция на плоскость основания, , ВД - проекция на плоскость основания. Так как АС > ВД, то > по свойству наклонных и их проекций, значит - большая диагональ призмы, - угол, образованный большей диагональю призмы и плоскостью основания. - угол, образованный меньшей диагональю призмы и плоскостью основания. По условию =30º, = 45º. Из ∆, (=90º) АС = 12 см, =, = - по свойству катета, лежащего против угла 30º. = А А= 6 см.

Используя теорему Пифагора АС = , АС =

Из ∆, (=90º), , Δ - равнобедренный, ВД = = 6 см.

Объем призмы V = , где - площадь основания призмы, = - высота призмы. , . V = .

Ответ: .

Задача №7.

Осевое сечение конуса прямоугольный треугольник. Найдите площадь боковой поверхности конуса, если радиус основания конуса равен 5 см.

Решение.

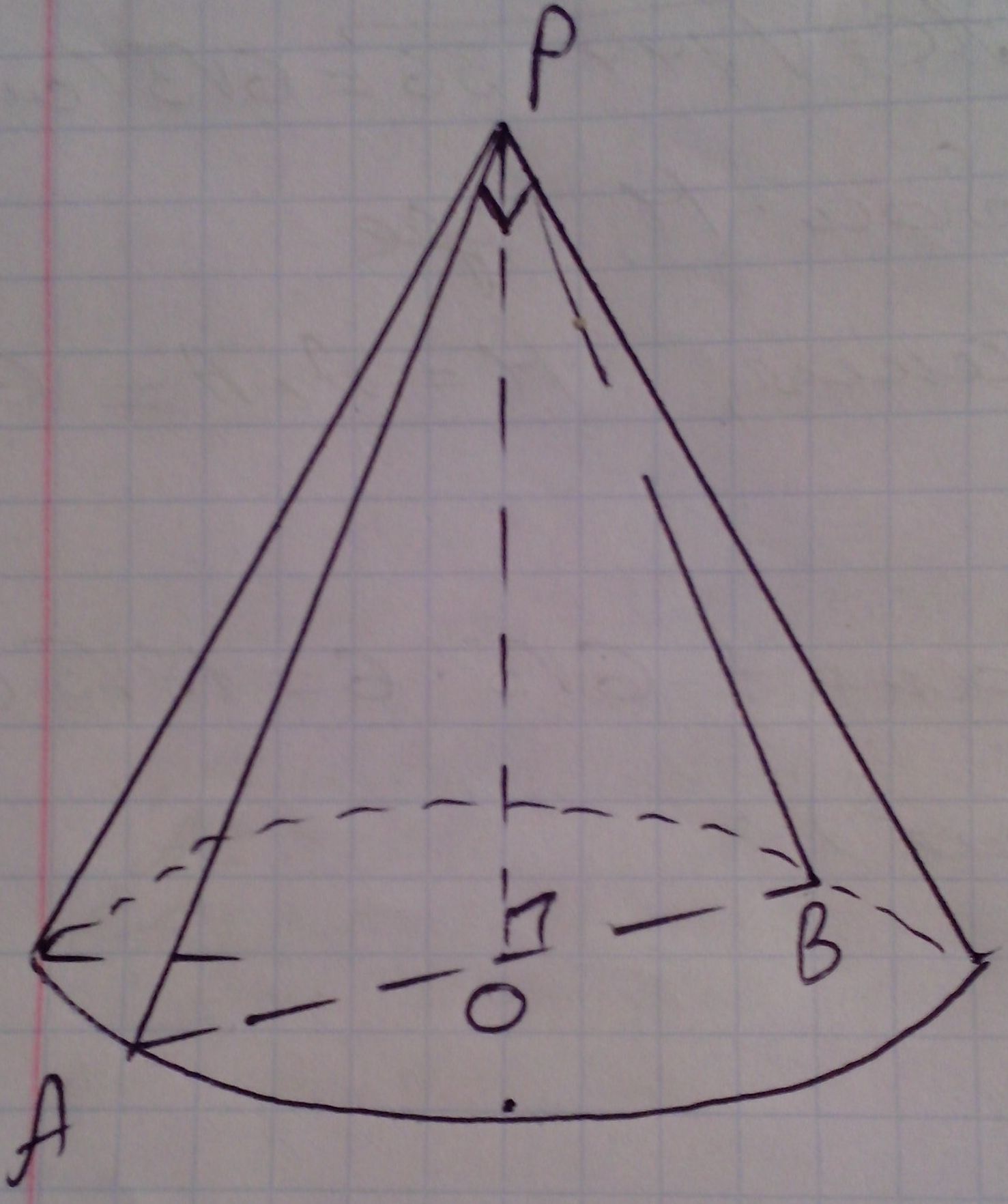
Пусть дан конус, точка О - центр его основания, РО - ось конуса, высота конуса. Построим сечение конуса - прямоугольный равнобедренный ∆АРВ, АРВ = 90º, АВ - диаметр основания конуса, РА=РВ - образующие. ОА = ОВ = 5 см (по условию) - радиусы основания конуса, АВ = 2·ОА, АВ = 2·5 = 10 (см).

Так как ∆АРВ - равнобедренный, PАB =PВA = 45º, как углы при основании равнобедренного треугольника. РА = АВ· cosPAB, PA = 10· cos45º = 10· =

Площадь боковой поверхности конуса , где R=ОА = 5 см, l = РА = см.

(см²).

Ответ: см².

Задача №8.

Осевое сечение конуса равносторонний треугольник со стороной 10 см. Найдите объем конуса.

Решение.

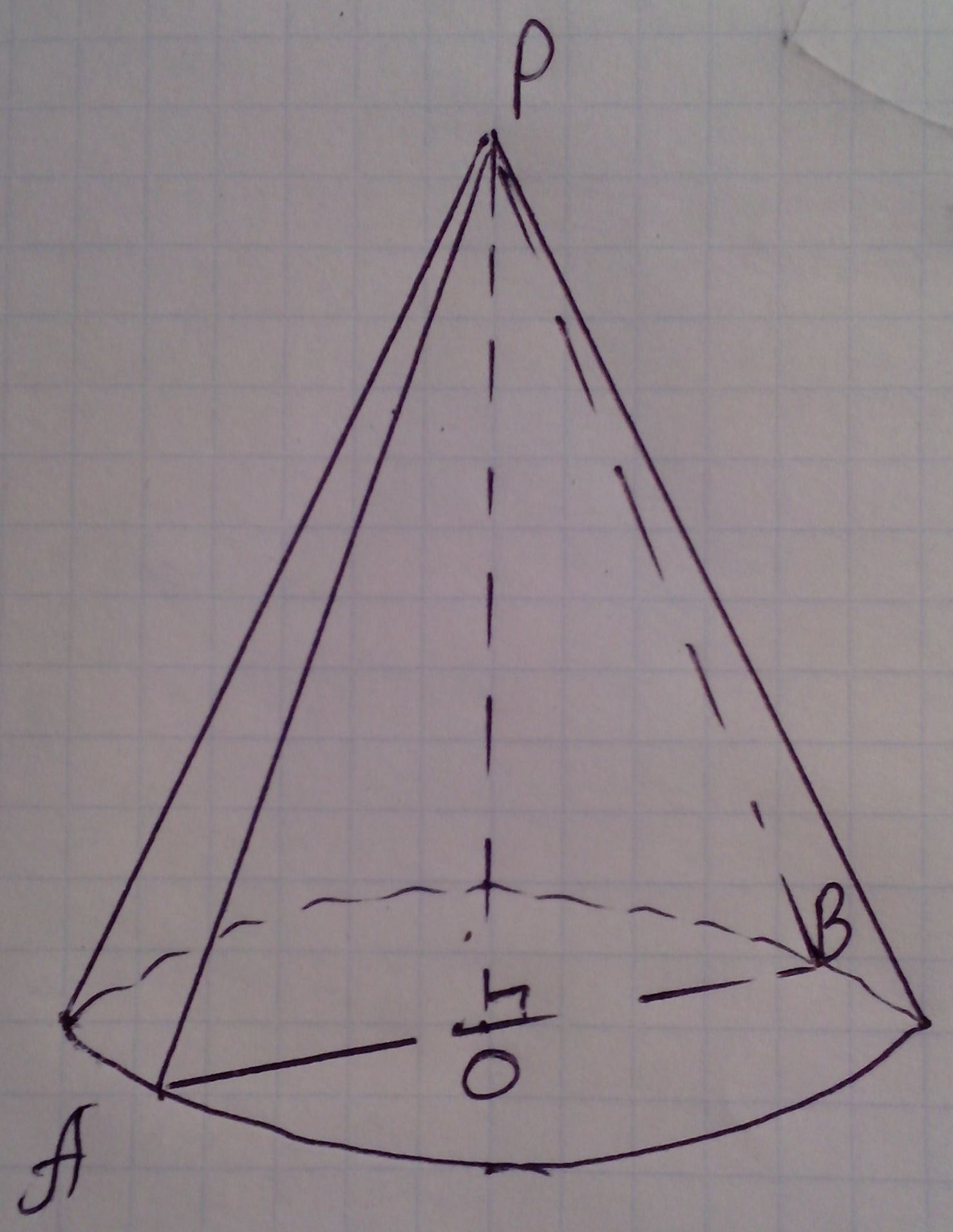
Пусть дан конус, точка О - центр его основания, РО - ось конуса, высота конуса. Построим сечение конуса - равносторонний ∆АРВ, РА=РВ=АВ = 10 см (по условию). РА, РВ - образующие конуса, РО(АРВ), АВ - диаметр конуса. АО=ОВ - радиусы основания, АО=ОВ =(см).

Из ΔРОА (РОА=90º), используя теорему Пифагора РО=,

РО = (см).

Объем конуса , где - площадь основания конуса. = , 25см². Тогда .

Ответ:

Задача №9.

Площадь боковой поверхности конуса равна 136см², а его образующая равна 17 см. Найдите объем конуса.

Решение.

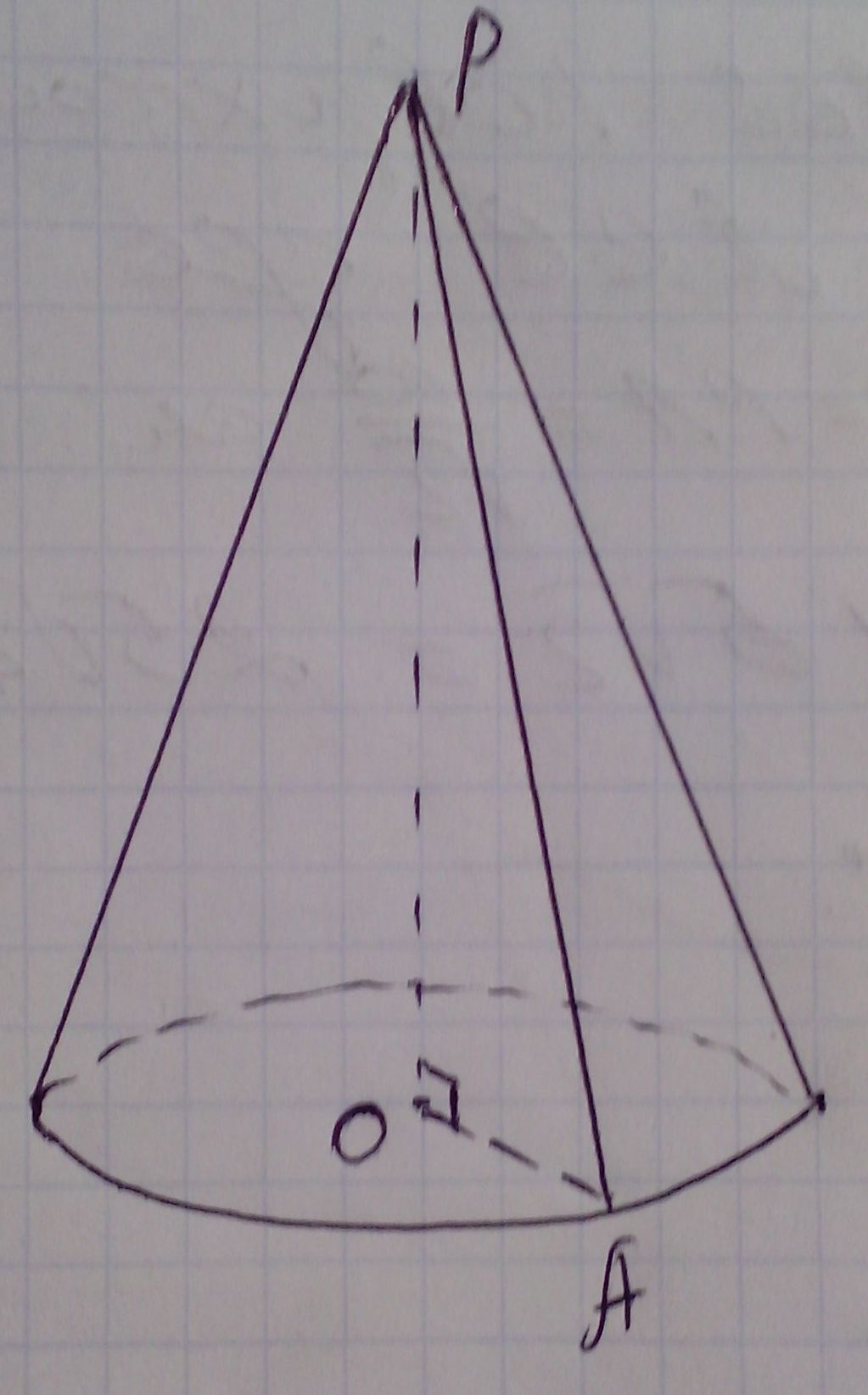
Пусть дан конус, точка О - центр его основания, РО - ось конуса, высота конуса, РА - образующая, ОА - радиус основания конуса.

По условию РА = 17 см, , где R = OA, l = РА, , отсюда ОА = , ОА = .

Из ∆РОА, (РОА=90º), используя теорему Пифагора РО=,

РО = (см).

Объем конуса , где - площадь основания конуса. = , 64см². Тогда .

Ответ:

Задача №10.

Площадь боковой поверхности конуса равна 65см², а его образующая равна 13см. Найдите объем конуса.

Решение.

Пусть дан конус, точка О - центр его основания, РО - ось конуса, высота конуса, РА - образующая, ОА - радиус основания конуса.

По условию РА = 13 см, , где R = OA, l = РА, , отсюда ОА = , ОА = .

Из ∆РОА, (РОА=90º), используя теорему Пифагора РО=,

РО = (см).

Объем конуса , где - площадь основания конуса. = , 25см². Тогда .

Ответ: